
Youla parametrizálás
A YOULA parametrizálás általános szabályozótervezési eljárást ad stabilis folyamatok irányítására. Bevezet egy ún. Q paramétert, amely a hagyományos visszacsatolt szabályozási struktúrában a beavatkozójel és az alapjel közötti átviteli függvénynek felel meg (1. ábra).
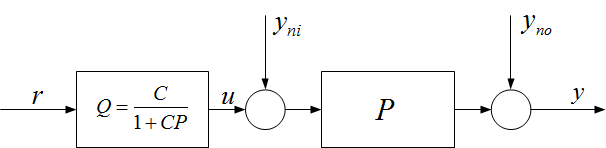
1. ábra A Youla paraméter
A nyitott körben optimális alapjelkövetés valósítható meg, ha a Q Youla paraméter a folyamat P átviteli függvényének inverzét valósítja meg. Ez a struktúra alkalmas az alapjel követésére, de nem képes a zavarások hatásának kiküszöbölésére. Ehhez a kört zárni kell. A zárt kör a 2. ábrán látható ún. IMC (Internal Model Control) struktúrában valósítható meg, amikoris a folyamat kimenőjele és a folyamat modellje kimenőjelének különbségi jelét csatoljuk vissza az alapjelhez.
2. ábra Szabályozás Youla paraméterrel IMC struktúrában
A 2. ábrán látható kapcsolásnak különböző egyenértékű változatai adhatók meg. A szabályozás bármilyen stabilis Q paraméter mellett stabilis lesz.
A hagyományos negatívan visszacsatolt körben a szabályozó megadható a Youla paraméterrel a 3. ábra szerint.
3. ábra A negatívan visszacsatolt szabályozási körben a szabályozó kifejezhető a Youla paraméterrel
Az optimális alapjelkövetés a gyakorlati esetek nagyrészében nem megvalósítható, mivel a folyamat P átviteli függvénye nem invertálható. (Nem invertálható például a holtidő, folytonos rendszerekben nem invertálhatók a rendszer jobb oldali zérusai, mivel invertálásukkal a szabályozóban labilitást okozó pólusok jönnének létre. Mintavételes rendszerben nem invertálhatók a folyamat egységkörön kívülre eső zérusai, illetve azok sem, amelyek az egységkörön belül a negatív valós tengely -1 ponthoz közel eső tartományába esnek.) Ilyenkor az átviteli függvényt fel kell bontani invertálható és nem invertálható részeinek szorzatára, és a Youla paramétert az invertálható rész inverzére kell beállítani. A kapcsolás kiegészíthető még az alapjel és a zavarójel szűrőkkel, amelyek biztosítják, hogy az alapjelkövetés és a zavarelhárítás dinamikája eltérő legyen (4. ábra). A szűrők átviteli tényezőinek értéke 1 kell legyen, hogy állandósult állapotban a kimenőjel pontosan kövesse az alapjelet, illetve teljesen kiküszöbölje a zavarás hatását.
4. ábra Youla parametrizált szabályozás szűrőkkel
További egyenértékű kapcsolást ad meg az 5. ábra.
5. ábra Egyenértékű Youla parametrizált szabályozás blokkvázlata
A szabályozótervezés tehát algoritmizálható eljárás: Fel kell bontani a folyamat átviteli függvényét invertálható és nem invertálható részre és meg kell adni a szűrők átviteli függvényeit. Ezután a szabályozás az ábrának megfelelően felépíthető.
A szűrőknek többszörös szerepük van: egyrészt segítségükkel előírható, hogy milyen legyen az alapjelkövetés, és milyen legyen a zavarelhárítás dinamikája. Azt mondjuk, hogy ezáltal a szabályozás két szabadságfokúvá vált. A szűrőkkel korlátozhatjuk a beavatkozójel nagyságát. A szűrőkkel javíthatjuk a szabályozás robusztusságát.
A különböző szabályozási algoritmusok a Youla parametrizálás speciális eseteinek tekinthetők.
A Youla parametrizálás alkalmazható mind folytonos, mind pedig mintavételes szabályozási rendszerekben.
Megjegyezzük, hogy a Youla parametrizálás csak stabilis folyamatok irányítására alkalmazható. (Labilis folyamatok irányítására az ún. polinomiális módszerek alkalmazhatók.)
Az alábbi Java applet bemutatja a folytonos Youla paraméterezett szabályozás működését.
Mintavételes rendszernél a folyamatot impulzusátviteli függvényével adjuk meg (6. ábra)
6. ábra Mintavételezett szabályozás
A Youla paraméterezett szabályozás blokkvázlatát ebben az esetben a 7. ábra mutatja.
7. ábra Mintavételezett rendszer Youla parametrizált szabályozásának blokkvázlata
Az alábbi Java applet szemlélteti a diszkrét Youla paraméterezett szabályozás működését.
Az impulzusátviteli függvényt felbontjuk a G+ kiejthető, és a G- nem kiejthető tényezőkre. d a diszkrét holtidőt jelenti, ami a fizikai holtidő és a mintavételezési idő hányadosa. A szabályozó algoritmus a folytonos esethez hasonlóan tervezhető.
Véges beállású szabályozás
A véges beállású szabályozó (dead-beat szabályozó) a kimenetnek az alapjelre való hibamentes beállását kívánja biztosítani a mintavételi idő egész számú többszöröse alatt. Feltételezzük, hogy a folyamat stabilis és az alapjel egységugrás. Megjegyezzük, hogy a véges beállású szabályozó akkor is megtervezhető - a bemutatottnál kissé bonyolultabb módon - ha a felsorolt feltételek nem teljesülnek.
A tervezés lényege, hogy előírjuk, hogy a szabályozott rendszer hogyan viselkedjen, azaz előírjuk a zárt rendszer $T\left(z\right)$ eredő átviteli függvényét. Véges beállású szabályozó esetén olyan eredő átviteli függvényt írunk elő, amely biztosítja a véges, megadott számú mintavételi lépés alatt történő beállást, azaz az egységugrás követésére $T\left(z\right)=z^{-d} $, ahol d a diszkrét holtidő, azaz $d={\rm entier}\left(T_{H} /T_{s} \right)+1$.
${C\left(z\right)G\left(z\right)\over 1+C\left(z\right)G\left(z\right)} =T\left(z\right)$
Ebből az egyenletből a szabályozó impulzusátviteli függvénye kifejezhető:
$C\left(z\right)={T\left(z\right)\over G\left(z\right)\left[1-T\left(z\right)\right]} $
Adjuk meg a G(z) impulzusátviteli függvényt számláló és nevezőpolinomjaival:
$G\left(z\right)={B\left(z\right)\over A\left(z\right)} {\kern 1pt} {\kern 1pt} {\kern 1pt} z^{-d} $
A szabályozó az alábbi összefüggéssel fejezhető ki:
$C\left(z\right)={A\left(z\right)\over B\left(z\right)\left(1-z^{-d} \right)} $
Mivel a szabályozó „kiejti” a folyamat pólusait, a pólusok csak stabilis pólusok lehetnek, tehát maga a folyamat a feltételezésünk szerint stabilis kell legyen. A szabályozó „kiejti” a folyamat zérusait is, tehát feltételezzük, hogy ezek „jó” zérusok, a komplex számsíkon a „szívgörbe” (lásd 94. oldal) belsejébe esnek.
Ha a folyamatnak vannak „rossz” zérusai is, azok kiejtésével (kompenzálásával) lengések jelennének meg a mintavételi pontok között. Az algoritmust ennek elkerülésére módosítanunk kell.
Válasszuk szét a folyamat impulzusátviteli függvénye számlálójának kiejtéssel kompenzálható illetve nem kompenzálható zérusait tartalmazó gyöktényezőit:
$B\left(z\right)=B_{+} \left(z\right)B_{-} \left(z\right)$
$B_{+} \left(z\right)$ tartalmazza a kompenzálható gyököket és $B_{-} \left(z\right)$ a nem kompenzálhatókat. Ha nem kompenzáljuk $B\left(z\right)$ valamelyik zérusát, akkor az közvetlenül meg fog jelenni a kimenőjelnek az alapjelre vonatkozó eredő átviteli függvényében. A szabályozóval szemben támasztott követelmény, hogy a szabályozás az egységugrás alapjelet statikus hiba nélkül kövesse. Ezért biztosítani kell, hogy $B_{-} \left(z\right)$ átviteli tényezője 1 legyen, vagyis $\left. B_{-} \left(z\right)\right|_{z=1} =1$ .
A következő lépésben olyan szabályozót tervezünk, amely nem kompenzálja az oszcillációt okozó zérust. A tervezésben a folyamat d holtidejét is figyelembe vesszük. A következőkben az impulzusátviteli függvényeket a $z^{-1} $ változó függvényeként adjuk meg.
A kimenetet a következő alakban írjuk elő:
$T\left(z^{-1} \right)=B_{-} \left(z^{-1} \right)\cdot z^{-d} $
A szakasz impulzusátviteli függvénye:
$G\left(z^{-1} \right)={B_{+} \left(z^{-1} \right)B_{-} \left(z^{-1} \right)\over A\left(z^{-1} \right)} \cdot z^{-d} $
Az eredő impulzusátviteli függvény a kimenőjel és az alapjel között:
${C\left(z^{-1} \right)G\left(z^{-1} \right)\over 1+C\left(z^{-1} \right)G\left(z^{-1} \right)} =T\left(z^{-1} \right)=B_{-} \left(z^{-1} \right)\cdot z^{-d} $
Átrendezve kapjuk a szabályozó impulzusátviteli függvényét:
$C\left(z^{-1} \right)={B_{-} \left(z^{-1} \right)\cdot z^{-d} \over G\left(z^{-1} \right)\left(1-B_{-} \left(z^{-1} \right)\cdot z^{-d} \right)} ={T\left(z^{-1} \right)\over G\left(z^{-1} \right)\left(1-T\left(z^{-1} \right)\right)} ,$
illetve figyelembe véve $G\left(z\right)$ felbontását
$C\left(z^{-1} \right)={A\left(z^{-1} \right)\over B_{+} \left(z^{-1} \right)\left(1-B_{-} \left(z^{-1} \right)\cdot z^{-d} \right)} $
A véges beállású szabályozó olyan speciális Youla parametrizált szabályozónak tekinthető, ahol nem alkalmazunk szűrőket, Rr=1 és Rn=1, és a Youla paraméter
$Q\left(z^{-1} \right)={A\left(z^{-1} \right)\over B_{+} \left(z^{-1} \right)} $
Megjegyezzük, hogy a Youla parametrizált szabályozás a szűrőkkel finomabban hangolható szabályozást képes biztosítani.
