| 3D printer |
See: 3D production technologies |
| A,B,C,D representation |
state space representation of systems: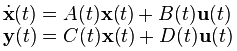 |
| absolute value |
(44) the value of signals in the real value domain
without phase difference; the amplitude of vector quantities |
| adaptive |
a system property which adjusts the system to the
circumstances (such as outside temperature), offsetting their undesired
effects |
| adaptivity |
a system property which adjusts the system to the
circumstances (such as outside temperature), offsetting their undesired effects |
| data mining |
(47) methodology for processing large quantities of
data. See also: Big Data. |
| additivity |
the sum of the values to be added is the same in all
grouping |
| Anyone |
(3) the curious reader of this e-book about systems
with a good but general secondary school level of understanding |
| pattern recognition |
the ability of living beings and machines to
recognise and learn identities and similarities. It is mainly applied to
visual and auditory patterns. Its computerised form is a branch of computer science. |
| shape |
(47) an umbrella term for signals and phenomena
which are or thought to be interrelated. It is the conceptual framework of
similarities or interacting properties of and between such signals and
phenomena. A branch of shape construction was applied in Gestalt psychology.
The terms pattern and scheme are also used in different
conceptual areas to express the same idea. Its technique is pattern
recognition. |
| algorithm |
(96) a mathematical program specifying a given procedure |
| steady state |
a state of rest where no change occurs. It is
generally reached after a change and can be maintained theoretically for an
unlimited period of time. |
| state |
the totality of the measurable and/or calculable variables
of the system enabling understanding and control the system. |
| state space |
the space of measurable and/or calculable signals
defining the system |
| amplitude |
(amplus ‘large, spacious’) the difference
(often the maximum difference) of variables from the steady
state |
| analytical function |
infinitely differentiable function that can be approximated
with its Taylor series. It is derived from the word analysis. |
| anticommutativity |
the property of a multiplication where the order of
the elements influences the result. AB ≠ BA |
| Aristotle |
(12, 37, 63)
(Aριστοτέλης; 384-322 BC),
one of the greatest philosophers and scientific thinkers of all time, the
ever-influential figure of European science who summarised the classical
scientific knowledge. |
| Arrow |
, Kenneth J. (12), economist, mathematician, winner
of the Nobel Prize in Economics in 1972. His impossibility theorem proves
that it is impossible to make a clear decision between multiple alternative
values while meeting certain “fair election” criteria. |
| association |
(12) the act of connecting concepts or thoughts. Association
is a key characteristic of cognitive activities and therefore it is a central
problem in brain research. |
| transparency |
clarity |
| transfer function |
(94) the fractional function describing the
transformation between the input and the output of the system. The roots of
the numerator are the zeros, and the roots of the denominator are the poles. |
| Banach spaces |
Banach, Stefan (1892-1945), Polish mathematician |
| input and output |
The input variable acts on the system. The system
reacts producing the output signal which affects its environment. |
| Bernoulli |
, Johann (1667-1748), member of the Bernoulli family
which produced many prominent mathematicians in the 17th and 18th
century. Apart from many other achievements, he raised the brachistochrone
problem (see there) which marked the origins of variation calculus. |
| Bernoulli brothers |
the Swiss Bernoulli family produced several
generations of excellent mathematicians and scientists. Two brothers are
highlighted here: Jacob Bernoulli (1654-1705) inventor of the Bernoulli
numbers and author of Ars Conjectandi, one of the oldest works on
mathematical probability, and Johann Bernoulli (1667-1748), (see there). |
| Big Data |
(46, 53) the methods used for processing extremely
large data sets considered to be unmanageable before the age of modern
computer technology, and for deriving conclusions from such data. |
| bijection |
the one-to-one correspondence between the elements
of two sets. |
| biology |
(βίος ‘life’, +
λογία ‘science’) the science of life and living
organisms |
| uncertainty |
an event, phenomenon or value which is not clearly
defined. The most important and theoretically most elaborate way to handle it
is the calculus of probabilities, but there are other approaches as well,
such as the concept of fuzzy sets, and the methods of evidence and the
estimation of certainty. Due to the nature of uncertainty, there is no
absolutely valid method to calculate it. Probabilities are approximated by
statistics. |
| Blaschke product |
complex analytical function in the open unit disk
with defined zeros. The products created this way give the function the shape
where the poles of the transfer function describing the system process are the
roots and the absolute values of the distance from the roots indicate the
distance from the singular (e.g. unstable) behaviour of the system. Blaschke
products are closely related to Hardy spaces and thus to the calculation
procedures of modern control theory. By the way, Wilhelm Blaschke (1885-1962)
was an Austrian mathematician whose career had inglorious periods. |
| Bode plot |
A method which provides a clear graphic
representation of the behaviour of a single-input-single-output system. The
plot shows magnitude (amplitude change) and phase shift separately on a
logarithmic scale versus frequency. It was first used by American engineer
Hendrik Wade Bode in the 1930s. |
| Bolyai-Lobachevsky geometry |
hyperbolic geometry named after the inventors of
Non-Euclidean geometry |
| brachistochrone |
(85) (βράχιστος
χρόνος ‘the shortest time’) the brachistochrone
curve is the curve on which a body slides in the shortest time under gravity.
J. Bernoulli published this problem in Acta Eruditorum, the first
international scientific journal, inviting the greatest mathematicians of the
age to contribute to the solution. The problem and its solution method was
the starting point of the calculus of variations and optimization tasks. |
| Cauchy |
, Augustin-Louis (1789-1857), French mathematician
who introduced clear and rigorous methods to discussing mathematical analysis.
Of his remarkable scientific achievements systems theory primarily uses the
Cauchy sequences (see: Banach spaces). |
| control objective |
(85) description representing the objective of the
system’s operation (see: optimisation) |
| conservation |
(62) maintaining some system properties during
motion (e.g. conservation of energy) |
| damping |
the reduction of the amplitude (volume, strength,
impact) of signals |
| group theory |
(78) a special concept of mathematical structures
which groups algebraic elements with identical characteristics to enable
transformations between them. Group theory is primarily associated with the
legendary figure of Galois (see there) but was also shaped by many
outstanding mathematicians throughout the history of algebra. Major
contributions include achievements of Klein in geometry and Lie in algebra
which have become part of the basic methodology of systems theory.
Transformation procedures make group theory relevant not only to mathematics
but also to all other fields of science and practice concerned with formal
transformations, such as chemistry. |
| Darwin |
, Charles (1809-1882) (28), the most influential
initiator of modern scientific thought. His main work is the theory of
evolution. In addition to providing an explanation to the origin of species,
the theory largely contributed to the research of systems and phenomena in
the widest sense. |
| Descartes |
, René (1596-1650) (42, 73, 80), one of the most
prominent pioneers of the philosophy of the Age of Enlightenment, a rational
thinker who had an enormous impact on science history by connecting geometry
and mathematics on a new basis, inventing the coordinate system (named after
him) and laying the foundations of analytic geometry. |
| Cartesian coordinate system |
orthogonal coordinate system in which measures are
the distances between the points |
| deterministic |
(88) a type of process determined by causality |
| student |
(3) undergraduate student or student with a
bachelor’s degree who is interested in the topic |
| differential equation |
(31, 50, 72) mathematics describing the relations
between changes in phenomena. It was first applied to describe the relation
between the distance, speed and acceleration in Newtonian mechanics. In
essence, it decomposes changes into small linear sections and calculates
their relations. |
| differentiability |
(50) the ability to approximate continuous processes
using a linear function, that is, at any point the difference between the
tangent and the next points can be arbitrarily small |
| differential operator |
the symbolic operation and notation of differential
calculus |
| differential calculus |
(85) perhaps the most important method of the system
approach, the revolutionary scientific theory of the Modern Age. It decomposes
the changes into small proportional steps and transforms them into a
generalising symbolic tool, the calculus, which enables the calculation of
any type of change. Although many great thinkers contributed to it in the
past and many more developed it further later on, differential calculus was
created by Newton and Leibniz competing for priority. |
| differentia specifica |
(12) the property characterising the difference
between groups deemed to be similar in certain aspects |
| digital |
a form expressed with numbers; as opposed to
analogue which expresses phenomena by words, pictures or sounds. |
| digitalisation |
(40, 52) the transformation of a phenomenon measured
and recorded in any form into a numerically scaled form. The quality of the
digitalised form (i.e. its fidelity to the original) depends on the fineness
and density of the scaling measure, such as resolution in the case of
digitalised images (the number of pixels, images per surface units, colour
range) |
| dimension |
(71, 73, 77) the least number of factors required to
determine phenomena or processes. In the Cartesian coordinate system
dimensions are the scale values necessary to determine the position of
individual points. In the usual determination of positions two dimensions are
used on the plane and three in space. In general, however, the term is used
as a definitive key characteristic in any relation or interaction. The word
stems from the term (to) measure. |
| dynamics |
(14) (δύναμαι ‘to
be able’) the science of motion and its relations |
| disharmony |
lack of harmony, deviation from a sequence |
| discrete |
not continuous, e.g. sampled. Discrete mathematics
traditionally include graph theory, combinatorics, game theory, the theory of
algorithms, cryptography, mathematical logic, set theory, number theory,
algebra and the branch of geometry which deals with defined shapes. |
| dissipation |
disappearance. In irreversible processes the part
(usually heat) of the energy that is lost during transformation. The
theoretical framework is included in the second law of thermodynamics.
Dissipation is a typical entropy-increasing phenomenon. |
| dissipation |
disappearance. In completely irreversible processes
the part (usually heat) of the energy that is lost during transformation. The
theoretical framework of the process is included in the second law of
thermodynamics. Dissipation is a typical entropy-increasing phenomenon. |
| EEG |
(74) electroencephalogram or encephalography; the
monitoring and recording of brain activity. |
| balance |
(25), (50, 59, 61, 63) or equilibrium. A basic
characteristic of systems; the completeness of the closely related units of
different system elements. The concept is based on the equilibrium of the
pans of a balance scale and is extended to the relations of mass and energy,
economic values, elementary particles and the entire system of the universe
governing thinking and models in these areas. |
| unit circle |
(80, 94) a special area on the complex plane
including its circumference which serves as the basis for function inversion.
Certain properties of the infinite complex plane can be easily calculated if
transformed into the unit circle (e.g. Hardy spaces). The unit circle can be
generalised to the unit sphere and other similar entities in higher dimension
problems. |
| Einstein |
, Albert (1879-1955), physicist who developed the
special and general theories of relativity and greatly influenced modern
physics and worldview. |
| ECG |
(74) or EKG, electrocardiogram; the monitoring and
recording of heart activity. |
| ellipse |
(78) see: conic sections |
| energy |
(60, 63) (εν ‘at’ +
έργον ‘work’), the capacity for doing work or
triggering change. The physical property of bodies exposed
to four fundamental interactions: gravitational, electromagnetic, strong and
weak interactions. Everyday practice is influenced by the first two
interactions, while the last two govern the atomic world and its relations
with the first two interactions. |
| entropy |
(18, 40, 68) (en ‘in’ + trope ‘a
turning, a transformation’) a system’s ability to transform in itself. It
describes transformations in thermodynamic properties and information content
and their possible directions. It is the measure of the order and disorder
characterising multi-element systems. The concept was created in
thermodynamics to describe the increase or decrease of the order of molecules
during the transfer of heat. |
| epigenetics |
(67, 69) the study of factors completing and
modifying heritable processes, and of the influence and heritability of
external processes. It is primarily a biological field of science but it can
be generalised to e.g. social processes as well. |
| epistemology |
(ἐπιστήμη
‘knowledge’) the methodology of gaining knowledge and the criticism of this
methodology. |
| Erlangen program |
(71) the main work of Felix Klein in which he
systematised the traditional and possible new geometries on the basis of
group theory. This laid the foundations of all the ideas and methods related
to spaces which are used in modern systems theory and which is the very
subject of this e-book. Klein wrote the Erlangen program as his inaugural
lecture but ultimately presented a different one. |
| emotions |
(8) all the emotional effects that influence the
decisions and reactions of living beings, particularly of humans, and that
can only be integrated into process models with quality markers. Typical
examples include deep anger, great happiness, terrible fear, concentrated
attention etc. |
| Escher |
, Maurits Cornelis (1898-1972), Dutch graphic artist
whose works first focused on natural forms, then architectural elements,
primarily floor patterns. His influential art combined these patterns in
complex geometric compositions with significant artistic and conceptual
effect. |
| aesthetics |
(αἰσθητικός
‘perceptive’), The branch of philosophy primarily dealing with the perception
of the quality of works, beauty and other quality properties. |
| ether |
(63) a mythological air-like medium, an ancient
element formerly thought to be the medium of electromagnetic phenomena |
| ethics |
(4) (ἦθος ‘moral character’),
the discipline concerned with what is morally right and wrong |
| Euclid |
(80, 94) (Εὐκλείδης,
fl. 300 BC), Alexandrian mathematician. His work Elements is
considered to be the foundation of geometry. It provides a summary of the
geometrical knowledge of the time and still defines the framework of
mathematical argumentation (theorem - proof), so its impact goes beyond
geometry. Euclid also contributed to number theory, primarily in the
methodology of partitioning. The more than 2000-year-old geometric results
and methods constitute the Euclidean geometry. The origins of non-Euclidean
geometry in the 19th century came from Euclid’s fifth postulate: the
definition of parallels (see: Bolyai-Lobachevsky geometry) |
| Eulerian |
, Leonhard (1707-1783), mathematician and physicist,
influential scientist of the St. Petersburg and Berlin schools. He
significantly contributed to the number theory, complex functions and other
areas of mathematics, his works are still fundamental in hydrodynamics and
other fields of mechanics (e.g. buckling). |
| Euler |
, Leonhard (1707-1783), mathematician and physicist,
influential figure of the St. Petersburg and Berlin schools. He significantly
contributed to the number theory, complex functions and other areas of
mathematics, his works are still fundamental in hydrodynamics and other
fields of mechanics (e.g. buckling) |
| evolution |
(23,28, 77) (ex ‘out’ + volvere ‘to
roll’) the continuous, uninterrupted process of changes, generally from the
simpler to the more complex. This e-book also adopts a Darwinian approach. |
| exponential |
(ex ‘forth’ + ponere ‘to put’), used
for processes, functions where the variable is in the exponent. The negative
exponent indicates a decreasing process, the positive exponent a rapidly
increasing process. The term exponential refers to the latter
(exponential explosion). |
| factorisation |
resolution into factors |
| phase angle |
(41) the relationship between signals that belong
together; the representation of differences of effects in time and space in a
coordinate system. |
| black box |
(48) when the internal operation of a system is
unknown, black box is a model about which the only sources of information are
the input and the output. |
| Felix Klein |
, Felix (1849-1925) (71), author of the geometric
interpretation of group theory. He summarised traditional and new geometric
field theories into a unified system which made him one of the founders of
modern mathematical thinking. His main work is the Erlangen program. |
| half plane |
the half of the infinite complex plane representing
stable or unstable processes |
| Enlightenment |
(73) intellectual movement of the 17th and 18th
centuries in Europe following the Renaissance. A critical approach resulting
in the freedom from the social and philosophical ties of former ages. The
foundations of our modern system of values and systems approach are rooted in
the Enlightenment. |
| philosophy |
(1) from the perspective of system science: the
search for relationships |
| physical model |
the representation of systems with physical elements
of similar behaviour |
| phlogiston |
(63) (φλόξ ‘flame, blaze’),
hypothetical (false) principle of combustion accepted in the 17th century claiming
that all combustible substances have a volatile constituent released as flame
in combustion. |
| concept |
(2) term summarising and representing phenomena |
| process |
the course of change in systems |
| contiguous |
operating without interruptions |
| source |
the original, starting point of any phenomenon |
| Fourier |
, Jean-Baptiste Joseph (1768-1830) (31). While
studying thermal conduction he invented the Fourier series (the fact that all
changes can be expanded into an infinite series of harmonic components) which
initiated the still prolific development of the mathematics and physics of
frequency analysis. He is also credited for the discovery of the greenhouse
effect. |
| Fourier-Laplace transformations |
the transformation of processes changing over time
into the frequency domain, and the reverse of this operation. The Laplace
transformation is the differential operator form of the Fourier
transformation and thus a useful tool to do calculations with algebraic
equations. |
| Fourier series |
the decomposition and representation of phenomena in
the series of frequency components |
| fractional transformation |
decomposing a function into product terms |
| frequency |
(19, 31,74, 92) (frequens ‘numerous, crowded,
populous’) the number of times of phenomenon occurs |
| frequencies |
(19, 31,74, 92) (frequens ‘numerous, crowded,
populous’) the number of times of phenomenon occurs |
| course of a frequency function |
the representation of phenomena as a function of
frequencies |
| fuzzy |
A popular tool for handling underdetermined
phenomena and sets with uncertain borders. It describes quantity with
quality. It is commonly used for the calculation of uncertainties. Its
relation to certain interpretations of probability calculus is disputed. |
| Galilei |
, Galileo (1564-1642) (125), a legendary figure of
renaissance science and research based on observations. He made fundamental
contributions to the sciences of motion and astronomy, and to the emergence
of the Newtonian approach. |
| Galois |
, Évariste (1811-1832), eminent mathematician who
died at the age of 20 from wounds suffered in a duel. Studying the roots of
fifth and higher degree equations he created an important pillar of abstract
algebra, the group theory, a unified framework for problems that can be
handled with the same operations. |
| Galois group theory |
, Évariste (1811-1832), eminent mathematician who
died at the age of 20 from wounds suffered in a duel. Studying the roots of
fifth and higher degree equations he created an important pillar of abstract
algebra, the group theory, a unified framework for problems that can be
handled with the same operations. |
| Gauss |
, Johann Carl Friedrich (1777-1855), mathematician,
scientist and astronomer, also referred to as Princeps mathematicorum
(‘the foremost of mathematicians’). He was a pioneer in several branches of
mathematics, including number theory, analysis and differential geometry. He
made major discoveries in astronomy, magnetism and optics. As a practical
geometer he was a significant contributor to geometry. His role in
influencing non-Euclidean geometries is disputed. |
| genetics |
(69) (γένεσις
‘origin’), the study of biological heredity that can be generalised to deal
with social matters. |
| genus proximum |
(12) when talking about a phenomenon classified into
a group, genus proximum means the nearest group. Such classification usually
takes place in a hierarchical order (see: similarity). |
| geometry |
(13) a separate branch of mathematics dealing with
the properties and relationships of shapes. The term originally referred to
the measurement of land. |
| gnomonic |
(75) (γνῶσις
‘knowledge’), a type of map projection in cartography used for
showing the length of flight paths. |
| Gram matrix |
a matrix created from the inner products of vectors
in linear spaces. It provides covariance, that is, the properties of
interacting behaviours, such as the independence of vectors from each other
or the basic relationships of controllability and observability in control
theory. |
| Guru |
(3) a PhD level reader who is dealing with systems
at an advanced level in possession of deep mathematical knowledge |
| H_2 |
in modern systems theory the integral measure of the
qualitative behaviour of a system; the norm of a system represented in the
Hardy space |
| H_inf |
norm calculated in the Hardy space based on the
square integral of the given phenomenon |
| set |
as a mathematical concept it is a collection of
elements with specific common properties |
| net |
general term in graph theory for interconnected
systems. The logical net is used for considering multiple effects, generally
represented also in a graphical form |
| Hamilton |
, William Rowan (1805-1865) (31, 63, 86), Irish
mathematician and physicist who created the uniform general mathematical
representation of Newtonian mechanics. His equations serve as the basis for
calculating the widest range of dynamic phenomena e.g. in systems theory,
including modern control theory and quantum theory. He made major
contributions to optics and astronomy and he invented quaternions (the
dynamics of complex elements consisting of four components; see there) which
gained their true significance in quantum physics. |
| Hamiltonian equations |
formulas, explanations separately |
| Hankel |
, Hermann (1839-1873), German mathematician who
worked together with many eminent contemporary mathematicians. He is best
known for his contribution to linear algebra. |
| Hankel matrix |
a square matrix which is symmetric with respect to
the main diagonal. It projects processes to the past and thus serves as a
hidden Markov process to determine the state matrix |
| Hardy |
, Godfrey Harold (1877-1947) (80, 82), British
mathematician with a major influence on number theory and mathematical
analysis. In the field of number theory he worked in legendary collaboration
with Indian mathematician Ramajunan who said some of his theorems came to him
in dreams. Hardy’s remarks on the beauty of mathematics, the ideal of
mathematicians’ interest is frequently quoted. Frigyes Riesz named after him
the spaces (see: Hardy spaces) which have practical significance in modern
systems theory as they calculate the quality norms of holomorphic (i.e.
complexly differentiable in the complex space) systems. |
| Hardy spaces |
in modern systems theory the finite space of
processes represented by analytical functions. It can be isometrically
represented in frequency and time space, which makes it particularly suitable
for determining system stability, robust stability domains and optimal
relations. |
| harmony |
(24) (harmonia ‘agreement, concord of
sounds’) |
| 3D production technologies |
(33) technology using the idea and technique of
inkjet printers. 3D objects are created by putting special liquid but quickly
solidifying material (typically plastic or metal) on a surface in several
layers. A special area is called 3D bioprinting which experiments with
printing biological tissues and cells. |
| Harvey |
, William (1578-1657) (37), English physician and
surgeon credited for the description of systemic circulation. His theory had
many precursors; some argue that Arab scholars had already known it in the
European Middle Ages. |
| efficiency |
the relationship between the energy or work put into
and coming out of a system. |
| Hilbert space |
vector space where scalar multiplications are
defined; i.e. a space where the norm can be fully determined by scalar
multiplications. It was named after Hilbert by Neumann whose work made it a
key calculation space in quantum theory. |
| hyperbola |
(78) a conic section formed by a plane which
intersects both cones of a double cone except for the vertex. In such
surfaces geometry, more specifically the straight lines passing through a
single point show properties that deviate from the Euclidean plane, alter the
concept of parallelism and the sum of angles of triangles. Hyperbolic
surfaces had an important role in the world view ruled by Einstein's gravity
theory but they also opened up new perspectives in the geometric aspects of
mathematics. |
| hyperbolic |
(78) a conic section formed by a plane which
intersects both cones of a double cone except for the vertex. In such
surfaces geometry, more specifically the straight lines passing through a
single point show properties that deviate from the Euclidean plane, alter the
concept of parallelism and the sum of angles of triangles. Hyperbolic
surfaces had an important role in the world view ruled by Einstein's gravity
theory but they also opened up new perspectives in the geometric aspects of
mathematics. |
| hyperbolic function |
functions defined similarly to trigonometric
functions but while the latter type of functions defines a circle, hyperbolic
functions define hyperbolas. Their signs are similar too: sinh, etc. They
play an important role in the description of physical processes. They were
first used for describing catenaries (cable or chain curves). |
| hyperbolic geometry |
Non-Euclidean geometry in which the parallel
postulate is invalid. The concept is primarily credited to Bolyai and
Lobachevsky but they had many important precursors. |
| hyper matrix |
a matrix whose elements are also matrices. Hyper
matrices are particularly important for the description of processes related
to partitioned and connected elements. |
| hyperstable |
stable in the broad domain of system
parameters |
| holistic |
(21)(holos ‘whole’) an approach which
considers the examined system as a whole and in context, similarly to a
medical specialist who also considers all other conditions of the patient. |
| holography |
imaging technology which uses the wave nature and
interference phenomena of light to display three-dimensional images (hence
the name: holos ‘whole’ + graphia ‘description of’). It became
common with the emerging application of laser (coherent light having a
constant phase difference). Dénes Gábor (Dennis Gabor) was awarded the Nobel
Prize for inventing the holographic method. |
| holomorphic |
of the same or similar form |
| holomorphism |
of the same or similar form |
| homogeneity |
(homos ‘same’ + genos ‘kind’) uniformity
in general or in a specific aspect |
| homology |
(17), (47) (homos ‘same’ + logos ‘relation,
reasoning’) the order of a specific field of science; in theology it is the
Word. In algebra and particularly in geometry it is a necessary
characteristic of identical properties. |
| homolosine |
(75) equal-area map projection which compensates the
distortion of Mercator maps with sinusoidal transformations, resembling to
the flattened rind of a peeled orange. It is credited to American
cartographer John Paul Goode (1862-1932). |
| homomorphism |
(17), (47) (homos ‘same’ + morphe
‘form, shape’) see: similarity |
| thermal motion |
Brownian motion; the random motion of atoms and
molecules under the effect of thermal energy |
| thermodynamics |
(68) the branch of science concerned with the nature
of heat and its relationship with other forms of energy |
| strings |
(42) see: Pythagoras |
| Huyghens |
, Christiaan (1629-1695), Dutch scientist,
astronomer and physicist, one of the most prominent thinkers of the 17th
century. Inventor of the pendulum clock and other clockworks, discoverer of
several celestial bodies, pioneer in probability theory, mechanics and optics. |
| identification |
the determination of the nature, states and
properties of systems, and the related mathematical and computational methods |
| indentify |
the determination of the nature, states and
properties of systems, and the related mathematical and computational methods |
| time domain |
the space for describing the behaviour of systems in
time |
| infinitesimal |
(derived from finis ‘end’) separation. to
infinitely small parts, referring to the basic idea of differential and
integral calculus |
| information theory |
(68) the theory of transmitting and processing
communications and signals. The subject matter of mathematics, philosophy,
social science, electrical engineering and other technical fields of science. |
| input-output |
Signals marking the boundaries of a system |
| intension |
intention; the consideration of subjective factors
with the tool set of non-monotonic logic |
| inverse |
reciprocal; if multiplied with the original value
the product is the unit. |
| control |
(34, 84) the umbrella term for closed-loop and
open-loop control. Term usage varies by language and profession. |
| controllability |
(89) the requirement that a system should be movable
from its current state toward a desired state |
| irreversible |
(65, 88) not reversible. A typical example of
irreversible processes is the making of scrambled eggs. |
| epistemology |
the branch of philosophy dealing with the
methodology of gaining knowledge and the criticism of this methodology |
| isometric |
(isos ‘the same’) of the same measure; refers
to distance-preserving transformations |
| isomorphic |
of the same form or shape |
| Jacobi equation |
formula; relationship expressing the requirements of
a position of steady state in Lie algebras where the sum of the permutations
of algebraic formulas is zero, and the differential changes of elements (the
algebraic expressions used) mutually compensate for each other. With binary
multiplication and addition operations in an S algebra: (126) |
| game theory |
the theory of mathematical models of conflict and
cooperation between intelligent rational decision-makers. The field of study
was created by the publication of John von Neumann (János Neumann) in 1928. |
| signal |
(41) any form of reality originating from and
connecting processes that can be measured in some way. One of the most
generic concepts in system theory. |
| Kalman |
, Rudolf (1930-2016) (89) an outstanding scientist
of modern control theory and technology, inventor of the theory of filtering
noise affecting the elements to be controlled. Today, practically all
controlled devices contain such a filter or a variation of it. His
theoretical work is made complete by the mathematical definition of
controllability and observability. |
| Kálmán |
, Rudolf (1930-2016) (89) an outstanding scientist
of modern control theory and technology, inventor of the theory of filtering
noise affecting the elements to be controlled. Today, practically all
controlled devices contain such a filter or a variation of it. His
theoretical work is made complete by the mathematical definition of
controllability and observability. |
| Kalman filter |
an algorithm which continuously monitors the state
of a system and generates statistics from the collected data to separate information
related to system operation and noise. Feeding the results back to the
closed-loop control adapts system operation to the changing conditions. The
filter was first used for controlling flying objects, but today, due to the
development of signal processing equipment, it is used in most control
systems. |
| Kálmán filter |
an algorithm which continuously monitors the state
of a system and generates statistics from the collected data to separate
information related to system operation and noise. Feeding the results back
to the closed-loop control adapts system operation to the changing
conditions. The filter was first used for controlling flying objects, but
today, due to the development of signal processing equipment, it is used in
most control systems. |
| Kalman filters |
an algorithm which continuously monitors the state
of a system and generates statistics from the collected data to separate
information related to system operation and noise. Feeding the results back
to the closed-loop control adapts system operation to the changing
conditions. The filter was first used for controlling flying objects, but
today, due to the development of signal processing equipment, it is used in
most control systems. |
| characteristic equation |
equation defining the roots of polynomial
differential equations and algebraic equations of similar structure. It is
used to solve multiply differentiable analytical process equations (i.e.
equations that can be expressed as a Taylor series) which play a primary role
in systems theory. |
| Cartesian |
(80) relating to the works of René Descartes (from
the Latinized name: Cartesius). In geometry it refers to the orthogonal
coordinate system. |
| Cartesian, orthogonal |
(80) relating to the works of René Descartes (from
the Latinized name: Cartesius). In geometry it refers to the orthogonal
coordinate system. |
| cascade control |
the closed-loop control scheme of systems separated
to cascading stages. The term cascade refers to waterfall or fall in
general. |
| causality |
the principle of relationship between cause and
effect. In systems theory it is the concept that the present state depends on
previous states but it only has a limited influence on future. |
| frames |
the set structure of a given property in the control
of smart systems and other connection properties |
| cognitive sciences |
the interdisciplinary scientific investigation of
cognition, i.e. the mental process of knowing. It synthesizes the results of
psychology, sociology, linguistics, computer science and brain research. |
| complex |
consisting of interconnected parts. In mathematics
it refers to systems which express the quantities, values and the magnitude
and direction of signals in an integrated way. In complex plane
representation they are the coordinates of real and imaginary axes. In
dynamic systems the change of direction is given as a function of time or
frequency. |
| complex half-plane |
(41, 96) the plane described by real and imaginary
coordinates to represent a process. The term complex and the two
concepts of number refer to the representation of all phenomena which are
described by dual connections. Such dual connection is the representation of
the amplitude, magnitude and phase shift relations, frequency components and
vector quantities of the phenomenon. |
| complex plane |
(41, 96) the plane described by real and imaginary
coordinates to represent a process. The term complex and the two
concepts of number refer to the representation of all phenomena which are
described by dual connections. Such dual connection is the representation of
the amplitude, magnitude and phase shift relations, frequency components and
vector quantities of the phenomenon. |
| lumped parameter model |
in general, the model of a spatially distributed
system by concentrating it at a characteristic point. The most typical example
is the concentration of physical masses at their centre of gravity. |
| assignment of coordinates |
the assignment of defining measures to signals and
phenomena. Its elementary metaphor is the determination of distances with
units of length. |
| coordinate system |
(31,75) system used to determine the position of
points (coordinates) on the basis of geometric shapes. The concept evolved
from the generalisations of space for the purposes of geographical
positioning, so it has many historical precursors. It developed from the
mathematical representation of movement, primarily through the work of Fermat
and Descartes. The mathematical geometry of the orthogonal coordinate system
is referenced as Cartesian system in the relevant literature. |
| use of coordinates |
(42, 71, 73) operation aimed at the arrangement and
combination of quantities and symbols derived from them in a suitable
coordinate system. According to prominent algebraists this is what algebra is
all about. |
| plotting coordinates |
(42, 71, 73) operation aimed at the arrangement and
combination of quantities and symbols derived from them in a suitable
coordinate system. According to prominent algebraists this is what algebra is
all about. |
| covariance |
the coordinated movement of two different variables.
It is calculated by summing the products of the deviations of corresponding
values of the two variables from their respective means in statistics and
calculus of probabilities. |
| Cretan liar |
(9) paradox attributed to Epimenides: “All Cretans
are liars," says a Cretan. The paradox appears in many forms in
philosophy; even Gödel refers to it as the conceptual precursor of his
incompleteness theorem. |
| conic sections |
(78) shapes resulting from the intersection of the
surface of a cone or double cone with a plane. The types of conic sections
are the parabola, the ellipse, the hyperbola and the circle which is a
special type of the ellipse. |
| quantum theory |
(71, 86) a branch of modern physics concerned with
the investigation and explanation of phenomena at scales that are beyond the
scope of observation by traditional means. It is rooted in the observation
that below traditionally observed scales the change of certain phenomena is a
series of discrete rather than contiguous units. Quantum theory deals with
the similarities of matter and wave like behaviour, phenomena of particles
intertwined at elementary level (which show promising future prospects for
telecommunications), phenomena taking place under extreme physical conditions
such as absolute zero temperature or vacuum, so it deals with the microscopic
world which is the deep foundation of modern physics with the uncertainty
principle. |
| quantum phenomenon |
(71, 86) a branch of modern physics concerned with
the investigation and explanation of phenomena at scales that are beyond the
scope of observation by traditional means. It is rooted in the observation
that below traditionally observed scales the change of certain phenomena is a
series of discrete rather than contiguous units. Quantum theory deals with
the similarities of matter and wave like behaviour, phenomena of particles
intertwined at elementary level (which show promising future prospects for
telecommunications), phenomena taking place under extreme physical conditions
such as absolute zero temperature or vacuum, so it deals with the microscopic
world which is the deep foundation of modern physics with the uncertainty
principle. |
| quaternions |
the representation of interrelated sets comprised of
four phenomena; the duplication of complex representation. It was primarily
used for coordinating rotation, and later for exploiting the opportunities of
quantum phenomena in computer science while simultaneously using the quantum
properties of photons. The idea occurred to Hamilton while he was walking on
the riverside in Dublin, so he carved it into a stone there. At the same time
various scientists had similar ideas. |
| unstable |
not stable; able to lose stability in reaction to
even a small input |
| instability |
not stable; able to lose stability in reaction to
even a small input |
| Lagrange |
, Joseph-Louis (1736-1813) (85, 86) Italian-French
mathematician, the most important contributor to variational calculus,
inventor of the method of Lagrange multipliers, who redefined Newtonian
mechanics as a variational problem and thus promoted the Hamiltonian approach
which dominates modern physics. |
| Laguerre polynomials |
second order linear differential equations which
play a role in the quadratic assessments in system modelling and analysis |
| Laplace |
, Pierre-Simon (1749-1827) (31) mathematician and
astronomer whose work greatly reformed the traditional approach to mechanics
and the role of differential operators. He developed the Laplace
transformation, which is a main tool in the mathematical representation and
calculation of systems. He played an important part in statistics, the
development of Bayesian interpretation of probability. Among many other
results in astronomy, he was the first to suggest the possibility of black
holes. |
| Laplace transformation |
complex variable transformation between the time and
frequency domain used for analysing processes described as differential
equations with constant coefficients. Due to the linear characteristic, the
differential equation form can be replaced by algebraic equations which is
the basis of calculating roots (zeros and poles) that are of primary
importance in studying system behaviour. The convolution characteristic, on
the other hand, simplifies the calculation of the interaction, serial and
parallel connection of system elements. |
| Lebesgue |
, Henri (1875-1941) French mathematician best known
for developing the comprehensive theory of integration by extending the
measure theory. |
| Lebesgue spaces |
Banach spaces extended to various distance measures;
normed Euclidean spaces. The concepts can be traced back primarily to Frigyes
Riesz. Usually referred to as l spaces |
| Lie |
, Marius Sophus (1842-1899) Norwegian mathematician,
author of the transformation groups in group theory, including
anti-commutative algebras which express equilibrium relations. |
| Lie group |
transformation groups characterised by Lie algebras |
| linear |
(54, 55) proportional change: the addition of inputs
triggers addition of effects. Multiple linear effects can be simply added
together (superposition). |
| linear differential equation |
if the system is modelled with linear differential
equations, the zeros and poles are the extreme values of the solution of the
differential equation: at the input, this is the state where even the biggest
effect fails to trigger displacement and the system exhibits infinite
inertia; while at the output, this is the state where even the smallest
effect will trigger an unstoppable displacement causing instability. |
| linearity |
(linea ‘line’) a behaviour that can be
represented as a straight line. Its main characteristic is additivity (its
elements can be simply added together) |
| linearisation |
(67) an approximation procedure used to make the
representation of behaviours proportionate and additive and to simplify
calculations this way |
| logic |
(27) (λóγος ‘reason, idea, word’)
logical argumentation |
| logical |
(27) (λóγος ‘reason, idea,
word’) logical argumentation |
| logical functions |
functions where the relationships between variables
are described by logical operations |
| radar |
equipment used in detecting the position and movement
of objects by measuring the radio waves, sound waves and optical waves
reflected from the surface of such objects. Depending on the medium, object,
distance and other circumstances such equipment include a broad range of
devices from microscopes to astronomical telescopes. The reflections are
usually processed in the form of three-dimensional images. Originally, it was
part of the military technology but today it is widely accessible and applied
in a vast number of fields. |
| Manhattan distance |
a measure of distance in the grid layout of streets
in Manhattan, New York City |
| mathematical model |
the description of any system with mathematical
tools. These descriptive methods provide the essence of the generality of
system science. |
| MATHEMATICA |
(87) a fourth-generation programming language
conceived by Stephen Wolfram (1959-) to automate mathematical operations,
algorithms and graphical representations. |
| MATLAB |
(87) product of MathWorks, a company founded by Jack
Little and Cleve Moler in the USA in 1984. A fourth-generation programming
language designed to describe and display processes and capable of
translating verbally defined operations to digital procedures. Another
product of the company is Simulink, a special program for process
representation. |
| matrix operations |
matrix is a rectangular array of quantities,
functions or mathematical expressions. It can be analysed with the methods of
linear algebra with the deviations applied to the given task group. Matrix
operations are the main procedures for creating, analysing and operating
system models that can be described and approached with linear algebra. |
| Maxwell |
, James Clerk (1831-1879) (31, 60) the founder of
modern electrodynamics. In his equations he summarised the basic relations of
electricity and magnetism, and proved the mutuality and wave like
characteristics of the two spaces. He laid the foundations of the kinetic
theory of gases. |
| Maxwell equation |
(31) |
| Mayer |
, Julius Robert (1814-1878) (60) pioneer researcher
of thermal energy who discovered the equilibriums in mechanical and thermal
energy and enunciated the first law of thermodynamics. |
| observability |
(89) the requirement that system behaviour can be
traced back from the current state to the beginning of the examined effects.
This is a precondition for being able to filter out noises and control the
system based on its history. |
| conservation of energy |
(60, 61, 62) the principle stating that energy
remains constant regardless of the changes. |
| Mercator |
, Gerardus (1512-1594) (75), philosopher, mathematician,
cartographer. He is most known for his cylindrical map projection which
served sea navigation purposes because of its ability to represent routes as
straight lines that preserve the angles with the meridians. The projection
method, however, has the drawback that it distorts shapes in a way that they
appear larger toward the poles and smaller toward the Equator. |
| measure |
(36, 39) the measurable property of phenomena, such
as voltage or temperature |
| artificial intelligence |
(AI) (27, 103) the loosely defined umbrella term for
all systems that tries to represent human thinking through machines. Thus,
the term is used for relatively simple series of logical operations as well
as for programs performing complex cognitive tasks surpassing human abilities,
for the representation of cognitive activities, and even for the fantastic
concept of superintelligence. Independent branches include: pattern
recognition, robotics, natural language processing, machine translation,
brain games and machine learning. |
| metabolism |
(μεταβολή
‘change’) the chemical transformation processes between living cells; more
generally: any transformation affecting the essence or substance. |
| metaphor |
(6)
(μεταφορά ‘transfer’) the figurative
explanation of a phenomenon with another, similar one. |
| metamorphosis |
(61)
(μεταμόρφωσις
‘change of form’) a complete change of form or substance |
| quality |
a general concept of system features, such as
accuracy, settling speed or cost. Stability as a basic requirement is
usually treated separately. |
| sampling |
(53) measurement process where the states of the
system are measured at certain intervals or as a function of other factors (not
continuously) |
| modality |
(27) (modus ‘manner, measure’) a
characteristic of deduction processes which depend on certain additional
circumstances, such as time constraints, personal and group views, random
effects, and other restrictive or influencing physical relations or
assumptions. Modality is a system of circumstances in non-monotonic logics. |
| model |
the description of a system by means other than the
system itself, such as mathematical representation, physical reduction, the
omission of certain parts, or other systems that are better known and behave
similarly. A model is only a limited representation of the underlying system,
so efficiency needs to be checked in a separate examination. |
| Möbius |
,August Ferdinand (1790-1868) (80, 81, 82), a
pioneer of projective geometry and topology. He is famous for the Möbius
strip and the Möbius transformation. The latter is particularly important for
systems theory as it enables highly practical transformations using the group
properties of rotation, stretching and shrinking. |
| Möbius transformation |
the linear transformation of shapes through
rotation, stretching and shrinking. |
| negative half-plane |
see: complex variable |
| negative feedback |
see: feedback |
| non-monotonic logics |
a system which modifies simple logical relations by
involving in the logical chain tools which characterise the given changes,
relations, modalities and intensions and which usually use the techniques of
logic or perhaps probability calculus. |
| non-linear |
(54) different from linear; i.e. effects do not
change proportionately and do not simply add up. |
| neural |
(12) related to the nervous system. It primarily refers
to the biological nervous system applied to the models of simplified
mechanical systems based on the assumption that they operate along similar
principles (neural networks). |
| neural network |
computer structure modelling the nervous system in a
highly simplified way, primarily performing learning tasks. |
| neurology |
the branch of medical science that deals with the
nervous system |
| Newton |
, Isaac (1642-1726) (86) legendary figure of modern
scientific thinking best known for his landmark contributions to mechanics,
optics and mathematics. |
| Newtonian |
reference to Newton’s theories mainly relating to
the metaphorical use of motion as a basic phenomenon, the mathematical
modelling of dynamic phenomena primarily in the form of differential
equations, and to the concept of light as a corpuscular phenomenon. |
| Noether |
, Amalie Emmy (1882-1935), highly influential German
mathematician famous for her outstanding contributions to abstract algebra
and theoretical physics. |
| norm |
(39, 44) the measure of a property of a phenomenon,
or a characteristic calculated from measurement results; the basic value of
such a property defined from a certain aspect. This way, freezing point is a
norm of temperature, daily mean temperature is a norm for heating processes. |
| sink |
the opposite of source; a stream usually similar or
related to energy which becomes lost or absorbed in an area contained by a
closed curve. The original mathematical-physical image relates to the
phenomenon described by Gauss-Stokes formulas for processes flowing out from
and into the closed curve, the sum of which is zero in a position of rest. In
control theory, this role is played by the environment of the -1 point
representing feedback on the complex plane. |
| Nyquist |
, Harry (1889-1976), Swedish born American electrical
engineer who made landmark contributions to the pioneering activity of the
Bell Labs, primarily in relation to the problem of thermal noises and the
theory of closed-loop control. For his achievements in the latter area, the
amplitude-frequency representation in polar coordinates is called Nyquist
plot. |
| cause |
(69, 77) one of the most dubious problems of
philosophical and everyday thinking; the question whether a phenomenon is
caused by one or more other (usually successive) phenomena or by the simultaneous
interaction of more phenomena. |
| ontology |
(5) a branch of metaphysics dealing with the origins
of and ultimate relationship between phenomena. In information science it is
the formal naming, definition and classification of phenomena. |
| operator |
(48) from a technical point of view, operators are
mathematically defined models which represent the subject system. |
| optimal |
(80) the practice of influencing systems so that
they ensure certain desired quality requirements such as costs, speed,
acceleration, etc. |
| optimise |
(80) the practice of influencing systems so that
they ensure certain desired quality requirements such as costs, speed,
acceleration etc. |
| optimisation |
(80) the practice of influencing systems so that
they ensure certain desired quality requirements such as costs, speed,
acceleration etc. |
| orthogonal |
(77) (ὀρθός ‘straight’ +
γωνία ‘angle’) right-angled. In a more general
meaning, properties that do not interact with or are opposed to each
other. |
| orthogonality |
(77) (ὀρθός ‘straight’ +
γωνία ‘angle’) right-angled. In a more general
meaning, properties that do not interact with or are opposed to each
other. |
| self-regulating |
(49) an autonomous system that operates without
external control, such as any (healthy) biological function. A fundamental
principle of the idealised model of a market. |
| parabolas |
(78) see: conic sections |
| Paracelsus |
(61) Philippus Aureolus Theophrastus Bombastus von
Hohenheim (1493-1541), Renaissance physician, alchemist, astrologer and
mystic, one of the pioneer critics of dogmatic scientific thinking in the
Middle Ages but affected by contemporary mysticism. |
| parameter |
in mathematical expressions a constant or variable
which determines the uniqueness of the expression from the perspective of a
given problem |
| parametrisation |
the definition, measurement, replacement and
calculation of parameters; see: parameter |
| partial differential equations |
(72) differential equations representing the
behaviour of processes which can be described along certain variables. This
way, in relation to motion, they represent the elementary steps in changes
according to the individual coordinates and time. |
| parallel |
(56, 95) the relationship between systems or system
parts that can replace each other, such as the kidneys. |
| parallel postulate |
an ancient problem of Euclidean geometry: the
possibility of proving that parallels intersect each other only in infinity
(see: Non-Euclidean geometries) |
| Parseval |
, Marc-Antoine (1755-1836), French mathematician
primarily known for the theorem named after him. The theorem says that the
square of the coefficients of a function’s Fourier series is equal to the
square integral of the function in the time domain. It relates to the basic
characteristic of the identity of the two representations. |
| partitioning |
the act of dividing something into parts |
| PID |
(96, 97) the proportional-integral-derivative (PID)
control is the most common control structure used to set the permanent,
continuous behaviour of the system and its adaptation speed. |
| PID control |
(96, 97) the proportional-integral-derivative (PID)
control is the most common control structure used to set the permanent,
continuous behaviour of the system and its adaptation speed. |
| Pythagoras |
(42)
(Πυθαγόρας, ?570-?495 BC) Greek
philosopher, mathematician and mystic clouded by legends. Most importantly,
he contributed to science with his worldview deeply rooted in numbers and his
achievements related to triangles and string lengths which almost naturally
follow from this worldview. His mystical worldview spread in religious-like
teachings and organisations. |
| Platonic shapes |
(25) shapes bounded by congruent regular planes.
Figures in space to which ancient lore attributed symbolic, often mystical
meanings to refer to the regularities of the world and the exclusiveness of
such regularities. Five such three-dimensional shapes were identified and
taken as the representation of ancient elements by Platon and the Greeks, and
as the structure of the solar system by Kepler. |
| Poincaré torus |
the hyperbolic representation of Euclidean space
into the closed space of a circle or—in higher dimensions—spheres. It has a
fundamental role in the transformation interpretations of systems theory.
Although it was named after Poincaré, as one of the most important
contributors, the idea was elaborated by Italian mathematician Beltrami
before him and by Felix Klein in parallel to both of them. |
| Poisson bracket |
or Lie bracket; a sign used in Lie algebras to refer
to the difference of expressions and their non-commutative counterparts which
gives zero in a position of rest and a negative value in all other cases
indicating difference, such as transformation |
| polar coordinate |
vector coordinate; definition and representation by
amplitude and phase angle |
| polynomials |
algebraic expressions of two or more terms. They
consist of variables, numbers, sum of terms each of which is the product of a
constant and variables raised to nonnegative integral powers |
| pole |
the singularity points of functions representing
phenomena. In control engineering they mark the zeros of transfer function
denominators. |
| potential |
the ability to perform work; a type of energy |
| prediction |
(99) an outcome forecast on the basis of former
system behaviour or other preset knowledge |
| projective geometry |
the geometry and relations of shapes resulting from
various projections |
| PROLOG |
high-level programming language used for solving
problems that can be handled by logical methods |
| prosthesis |
(33) artificial objects used to replace missing body
parts such as teeth or bones |
| psychology |
(26) (ψυχή ‘breath, spirit,
soul’ + λογία ‘study of’) the scientific study of
mental processes and behaviour |
| registration |
(74) (from Latin regerere ‘to carry/bring
back’) the process of recording system states and phenomena in a traceable
way with the tools of the given phenomena or recording technique. This is how
registration (recording, logging) devices and modern digital data collection
techniques have evolved (the latter in close relation with data mining) |
| hidden Markov process |
a mass of information in which the Markovian
characteristics (i.e. the interdependency or non-interdependency of
phenomena, data and their probabilities) can only be revealed with suitable
algorithms. It is a typical tool in pattern recognition. |
| coprime integers |
or coprimes. Numbers with no common divisor other
than the unit |
| theory of relativity |
(63, 71, 77) special and general relativity theory
on space, time, the unity of the two, and the relative phenomena of
space-time (Einstein) |
| disorder |
(68) a concept related to entropy referring to the
presence or absence of a mathematical or objective structure |
| Renaissance |
(73) intellectual and artistic movement in Europe
between the 14th and 16th centuries, after the Middle Ages, characterised by
the revival of classical traditions and values. |
| representation |
(30, 74) As regards systems, the act of
representing a phenomenon with a selected behaviour that is similar in a
certain aspect. The most general representation of system phenomena is
mathematics |
| residue |
remainder. The value of an integral along a closed
curve. Its meaning becomes clear when interpreting the Gauss-Stokes’ Law
(see: Gauss-Stokes, sink). In systems theory residue is interpreted as a
confinable singularity on the complex plane. |
| robot |
partly or fully automated machine that performs
work. It derives from the Slavic word for work and was first used in
this sense by Karel Èapek in 1921. |
| robust |
(80, 81, 102) a system which preserves its key
properties (primarily its stability but also some other quality properties)
in a predefined domain of disturbances to a reasonable and also predefined
extent. |
| Shannon |
, Claude (1916-2001), American mathematician and
engineer who laid the foundations of information theory |
| SIMULINK |
(87) see: MATLAB |
| scaling |
(39, 71, 74) the classification of a phenomenon by
one of its measurable properties, e.g. the classification of temperature by
the measurements on the Celsius or Fahrenheit scale. |
| Sophus Lie |
, Marius Sophus (1842-1899) Norwegian mathematician,
author of the transformation groups in group theory, including
anti-commutative algebras which express equilibrium relations. |
| serial |
(56, 95) elements arranged in a series where any
element can change the system or render it inoperable if unconnected (e.g.
digestive system) |
| Spinoza |
, Baruch (1632-1677), Dutch-Jewish philosopher,
prominent figure of the Enlightenment, pioneer of religious criticism. He
identified God with Nature (Deus sive Natura) |
| stable |
(80, 82, 91, 93) the inclination of systems to find
a position of rest after a finite value of disturbance. A basic requirement
of system behaviour |
| stability |
(80, 82, 91, 93) the inclination of systems to find
a position of rest after a finite value of disturbance. A basic requirement
of system behaviour. |
| stationary |
characterised by unchanging behaviour |
| static |
not moving |
| statistics |
(47) the science of collecting, processing,
classifying and analysing data |
| Stokes’ law |
(Stokes-Gauss) the value of an integral along a
closed curve is zero, or corresponds to the source or sink represented within
the curve. In physics it refers to various flows, in systems theory it refers
to singularities within a given domain in the system. |
| closed-loop control |
(34, 52, 84) change introduced to a system with a
specific aim. As opposed to open-loop control, closed-loop control involves
feedback. Term usage varies by language (in Hungarian: szabályozás vs vezérlés
vs irányítás). |
| controllability (szabályozhatóság) |
(89) see: controllability (irányíthatóság) |
| computational linguistics |
the application of linguistic methods, including in
particular grammar, to computers and the use of such methods in computational
structures in order to analyse and generate texts. |
| voting |
the method for selecting the best candidate or the
best choice. Its dubious validity and clarity is long known. Condorcet proved
that no voting method can be free from inconsistencies or contradictions,
illustrating his claim through the conflict of decision by majority vote and
decision by comparing pairs. Similar reservations apply to decision-making
processes used in computer programming. |
| extreme (value) |
the first or last, largest or smallest, most
favourable or most unfavourable values in a series |
| personal freedom |
(7) a fundamental human right especially emphasised
in information society (cf. privacy, transparency) |
| syllogism |
(27)
(συλλογισμός
‘conclusion, inference’) a form of deductive reasoning. They were originally
defined by Aristotle and still serve as the basic structure of deductive
logical procedures and computer programs, such as the programming language
PROLOG. |
| symbols |
(6)
(σύμβολον ‘contrasting, comparing’)
something representing another thing by association or resemblance |
| symmetry |
(25) (συμ ‘together’ +
μετρία ‘measure’) similarity or balance among
systems or parts of a system |
| singular |
unique value or state: optimal, pessimal, unstable.
See: poles |
| singularity |
unique value or state: optimal, pessimal, unstable.
See: poles |
| stochastic |
(88) (στόχος ‘assumed,
alleged’) effects or processes that are or assumed to be random, uncertain
and of unspecified origin and nature |
| superposition |
(54) the simple linear cumulation of phenomena (see:
linear) |
| supremal |
upper limit. A term generally used to describe
spaces, separately from the term used for the maximum of a function. |
| supremum |
upper limit. A term generally used to describe
spaces, separately from the term used for the maximum of a function. |
| filtering |
in systems theory, the elimination of disturbances
affecting a process usually by separating the frequency or amplitude domain
of the useful signals and of the disturbances or by employing probability
calculus or statistical methods. See: Kalman filter |
| filter |
(46) in systems theory, calculation methods which
separate disturbances from the signals to be evaluated and controlled usually
employing probability calculus methods, mainly in frequency domains. |
| learning |
the statistical recording of the behaviour, states
and influence outcomes of systems and the analysis of such data with the
methods of probability calculus and logic |
| reserve |
the stand-by energy or energy-like state of a system
which is ready to use. See: potential energy |
| Taylor |
, Brook (1685-1731), English mathematician, author
of the series named after him. He also participated in the adjudication of
the Leibniz-Newton calculus controversy |
| Taylor series |
the power series of functions which can be
differentiated any times in the surrounding or domain of the examined point.
Most functions used in practice can be expressed or approximated as a Taylor
series which makes the method one of the most common practical tool for
calculations. |
| inertia |
(15) the tendency of bodies to change their state
only when acted on by an external force (from Latin iners ‘inactive’).
The concept of inertia is often used figuratively in many other fields, such
as in social sciences. The relations between inertia, mass and space-time
gained new interpretations in the general theory of relativity. |
| power |
(15, 63) In physics, power (symbol: P) is the speed
of performing work or transferring energy; the work done per unit time. In
dynamics, this work is the distance covered against a force, in all other
fields it is an analogous concept, e.g. temperature change |
| space |
(71, 72, 75, 79) the totality of phenomena and
processes connected by some regularity of a geometrical nature. It is
conceptually rooted in the experience of sight which is determined by
mathematics and physics in the Cartesian coordinate system using the
Euclidean rules. The generalisation of the concept is essential in thinking
about and doing calculations in systems, ensuring the most efficient approach
to modelling their operation. Formerly space was a central concept in making
maps for various purposes and designing buildings, now it determines medical
imaging and 3D production technologies. One of the most important
achievements in the development of scientific thought is our ability to place
phenomena in space. |
| spaces |
(71, 72, 75, 79) the totality of phenomena and
processes connected by some regularity of a geometrical nature. It is
conceptually rooted in the experience of sight which is determined by
mathematics and physics in the Cartesian coordinate system using the
Euclidean rules. The generalisation of the concept is essential in thinking
about and doing calculations in systems, ensuring the most efficient approach
to modelling their operation. Formerly space was a central concept in making
maps for various purposes and designing buildings, now it determines medical
imaging and 3D production technologies. One of the most important
achievements in the development of scientific thought is our ability to place
phenomena in space. |
| natural language |
spoken or written communication in any language that
has evolved naturally. Its translation into a form that can be processed by
computers is a central task of computational linguistics (see
there). |
| thermodynamics |
(59) (θέρμη ‘heat’ +
δύναμις ‘energetic force’) the term was
coined in the 19th century which shows that the actual relationship between
heat as a type of energy and heat as its scalable perceived effect was
discovered relatively late in the history of physics. The discovery has also
contributed to our understanding of the relationship between heat and motion. |
| Toeplitz matrix |
(see: XI) a diagonal-constant matrix in which the
entries along any diagonal parallel to the main diagonal are identical. The
form resembles the continuous playing of video recordings in different times
and places, this is why it is used to represent series of processes that take
place there and back in time. |
| Toeplitz |
, Otto (1881-1940) German-Jewish mathematician
mainly working in functional analysis, and the history and education of
mathematics |
| trajectory |
path and its graphical representation; the
representation of processes. (from Latin traicere ‘throw
across’) |
| trajectories |
path and its graphical representation; the
representation of processes. (from Latin traicere ‘throw
across’) |
| transformations |
(43) change of shape, especially from one
representation mode to another. In systems theory the most common type of
transformation is from the time domain to the frequency domain. |
| decision by vote |
see: voting |
| real numbers |
the infinite set of natural integers and fractions.
Its representation is the number line. |
| probability |
the expected chance of an event to occur.
Probability is the most important case of uncertainty definitions (e.g.
Fuzzy). Its most elaborate methodology is probability theory. See:
stochastic, fuzzy |
| probability theory |
(47) the calculation of the expected occurrence of
random events |
| calculus of variations |
(85) the selection of functions whose definite
integral takes an extreme value (minimum or maximum) in a set of functions
(functionals). Practically, this is the basic question in all optimisation
tasks. |
| vector spaces |
the space of vectors, that is, quantities that have
magnitude and direction (phase angle) |
| open-loop control |
(34,52, 84) operation usually by logical means and
without feedback. Term usage varies by language and profession. |
| Pope Alexander VI |
(1431-1503) (75), member of the Borgia family during
the Italian Renaissance who issued the bull granting Spain all lands to the
west and Portugal all lands to the east of the meridian lying halfway between
the Cape Verde islands and Haiti. |
| feedback |
(56, 90, 95) the most important element of
closed-loop controls; the return of information about impacts affecting a
process and their result to the process |
| Youla |
, Dante C. (1925-) (98) American electrical
engineer, best known for the parametrisation named after him and Kuèera. If a
stable control system is complemented with an element which aims to meet a
given quality property, the whole system’s stability needs to be revised and
recalibrated. This is done by Youla parametrisation which relies on the
coprime property of system elements (i.e. that their greatest common divisor
is 1) |
| Youla parametrisation |
the design of the parameters of the closed-loop
control and the stable system which satisfies its quality requirements |
| Youla-Kucera parametrisation |
See: Youla parametrisation |
| noise |
disadvantageous signal that disturbs the operation
of the system See: filter |
| noises, disturbances |
disadvantageous signal that disturbs the operation
of the system See: filter |
| closed-loop control |
see: feedback |
| disturbance |
(40, 95) any signal influencing the process but not
serving its purpose. Disturbances are usually stochastic |
| feedforward |
See: filtering |
| feedforward, cascade control |
See: filtering |
| zero |
(94) see: transfer function |
