System Book

Rendszer és modellje

A rendszer a valós világ egy része, amely kölcsönhatásban áll környezetével. A rendszer a környezetből jövő bemenőjelekre a kimenőjelekkel válaszol. A jel egy fizikai (biológiai, gazdasági, stb.) mennyiség vagy a mennyiség megváltozása, amely információt hordoz a vizsgált rendszer, a jelenség természetéről.

A modellalkotás a rendszerek vizsgálatának lényeges eleme. A modellezés a kísérleti kutatás, vizsgálódás eszköze, amelynek során a vizsgált rendszert egy másikkal helyettesítjük. A modell alapján tanulmányozhatjuk a rendszer viselkedését, tulajdonságait.

Sok esetben a valós rendszeren nem végezhetünk kísérleteket, mivel ezek túl költségesek lennének, vagy megzavarnák a rendszer működését. Sokszor a rendszer még nem is létezik, csak tervezzük a létrehozását, és a modellje alapján kívánjuk elemezni várható viselkedését.

A modellezés célja: 

• a rendszerek tulajdonságainak, viselkedésének elemzése, megértése (analízis)
• a rendszerek jövőbeli állapotának megjóslása (predikció),
• rendszertervezési feladatok megoldása (szintézis),
• a rendszerek minősítése (validálás).

A rendszer modellje valamilyen szempontból leírja a rendszer viselkedését. A rendszer modellje összegzi tudásunkat a rendszerről.

A modell lehet fizikai modell vagy matematikai modell.

Fizikai modell például a tényleges rendszer kicsinyített mása (pl. repülőgép-, autó-, hajó- vagy vasútmodell). A fizikai modell alapján a valóságos rendszer főbb tulajdonságai vizsgálhatók, lehetnek azonban olyan tulajdonságok is, amelyek a mérettől is függnek és a rendszer kicsinyített másán nem vizsgálhatók. Például a kicsinyített járműmodelleken a jármű haladásának tulajdonságai vizsgálhatók, de például az utasok kényelmét befolyásoló jelenségek kevésbé.

Egyes rendszerek között hasonlóságok, analógiák állapíthatók meg. Például egy mechanikai és villamos rendszer elemei és jelei megfeleltethetők egymásnak. Ennek alapján egy mechanikai rendszer vizsgálható villamos megfelelőjének elemzésével, vagy fordítva, egy villamos rendszer tulajdonságai megadhatók egyenértékű mechanikai modellje alapján. Az 1. ábra egy ellenállásból, induktivitásból és kondenzátorból álló villamos rendszert és egy tömegből, rugóból és folyadékcsillapításból álló mechanikai rendszert mutat. A villamos rendszer bemenőjele az u feszültség, kimenőjele az i áram (vagy a q töltés). A mechanikai rendszer bemenőjele az F erő, kimenőjele a h elmozdulás. A kimenőjel és a bemenőjel közötti összefüggést kívánjuk meghatározni.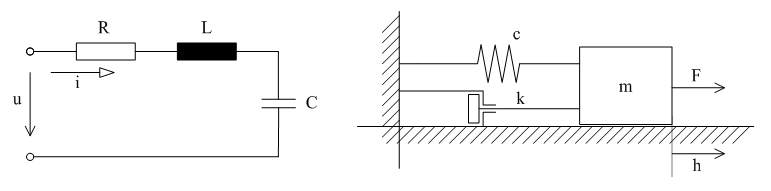

1. ábra Analóg, egymásnak megfeleltethető villamos és mechanikai rendszer

A villamos jelenségek sok szempontból hasonló viselkedést mutatnak a folyadékok áramlásához, így szemléltethetők a folyadékáramlás jelenségeinek vizsgálata alapján is.

A matematikai modell a rendszer viselkedését matematikai egyenletek formájában írja le. Segítségével analizálhatjuk a rendszer viselkedését anélkül, hogy a valóságos rendszeren kísérleteket végeznénk. A rendszer modellje alapján számításokat végezhetünk és numerikusan szimulálhatjuk a rendszer viselkedését. A rendszer modelljét használjuk fel a szabályozó tervezéséhez is.

Példaként adjuk meg az 1. ábrán látható villamos és mechanikai rendszerek matematikai leírását. A rendszerek viselkedése differenciálegyenletekkel írható le, amely a bemenőjel és annak megváltozásai (deriváltjai) és a kimenőjel és annak megváltozásai (deriváltjai) között ad meg összefüggést. A jel olyan mennyiség, amelynek információtartalma van. A villamos rendszer viselkedése az alábbi differenciálegyenlettel írható le:

$u=iR+L\frac{di}{dt} +\frac{1}{C} \int _{0}^{t}id\tau $ 

Ez az egyenlet azt fejezi ki, hogy az ellenálláson, az induktivitáson és a kapacitáson fellépő feszültségesések összege adja meg a hálózatra kapcsolt feszültséget. A villamos töltést jelöljük q-val, amely az áram integrálja (tekintsük most ezt kimenőjelnek). Ezzel a fenti egyenlet az alábbi alakban adható meg:

$u=L\frac{d^{2} q}{dt^{2} } +R\frac{dq}{dt} +\frac{1}{C} q $

A mechanikai rendszer differenciálegyenlete:

$F=m\frac{d^{2} h}{dt^{2} } +k\frac{dh}{dt} +ch $

ami azt fejezi ki, hogy a tömegre ható erők eredője, ami az F húzóerő, a sebességtől függő folyadékcsillapítás és az elmozdulástól függő rugóerő különbsége hozza létre a gyorsulást. Látható, hogy a villamos és a mechanikai rendszer viselkedését másodrendű differenciálegyenlet írja le. A két rendszerben az egymásnak megfelelő, analóg mennyiségek:

Jelöljük a bemenőjelet $u$-val, a kimenőjelet $y$-nal, a paraméterek értékét pedig $a_{0} ,a_{1} ,a_{2} $-vel. Mindkét rendszer matematikai egyenlete az alábbi differenciálegyenlettel írható le:

$a_{2} \frac{d^{2} y}{dt^{2} } +a_{1} \frac{dy}{dt} +a_{0} y=u $

Az egyenlet egy lehetséges megoldási módját kapjuk, ha kifejezzük a kimenőjel legmagasabb differenciálhányadosát (a mechanikai rendszer esetén a gyorsulást):

$\frac{d^{2} y}{dt^{2} } =\frac{1}{a_{2} } u-\frac{a_{1} }{a_{2} } \frac{dy}{dt} -\frac{a_{0} }{a_{2} } y $

A bemenőjel hirtelen változására először csak a gyorsulás változik, amely az idő előrehaladtával változtatja a sebességet, majd a sebességgel megváltozik az elmozdulás. (A sebesség a gyorsulásjel integrálásával, az elmozdulás a sebességjel integrálásával alakul ki.)

A blokkvázlatot, ami számítási algoritmus alapja is lehet a 2. ábra mutatja. A bemenőjel és a kezdeti feltételek megadásával az integrátor blokkok számítják az idő lefolyásával a kimenőjel deriváltját és a kimenőjel időbeli alakulását. (Az ábrán a zárójelben lévő felső index jelöli a deriváltakat.)

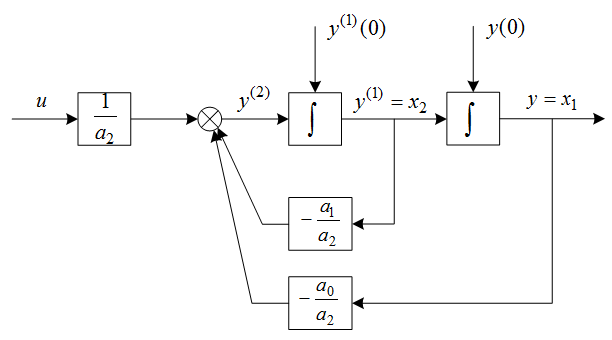
2. ábra Másodrendű differenciálegyenlet blokkvázlata

Az integrátorok kimenőjelei a rendszer szempontjából fontos mennyiségek (elmozdulás, sebesség, illetve elektromos töltés, áram), amelyek a rendszer ún. állapotai, értéküket a rendszerben végbement korábbi változások hatása alakítja ki, mondhatjuk, hogy memória jellegű tulajdonsággal rendelkeznek. A bemenőjel változására nem képesek hirtelen megváltozni, megváltozásuk fokozatosan következik be. Az állapotváltozókkal a másodrendű differenciálegyenlet két elsőrendű differenciálegyenletből álló rendszerré alakítható át. Ez a rendszer ún. állapotegyenlete.

$\frac{dx_{1} }{dt} =x_{2}$

$\frac{dx_{2} }{dt} =-\frac{a_{0} }{a_{2} } x_{1} -\frac{a_{1} }{a_{2} } x_{2} +\frac{1}{a_{2} } u $

$y=x_{1} $

A rendszer modellje alapján a rendszer viselkedése, válasza a bemenőjelre és a kezdeti feltételekre vizsgálható, számítható. A számítások egyszerűbb esetekben (lineáris egyenletek, jól meghatározott, analitikusan leírható bemenőjelek esetén) analitikusan elvégezhetők. Ezeket a számításokat könnyítik meg a különböző programnyelvek, így a modellezésre készült Matlab, a Mathematica, a SIMUL, vagy a logikai kapcsolatokra a Prolog.

Hivatkozások:

Levine (1996)

Szűcs (1970,1972)