
Az irányítás célja és célfüggvénye
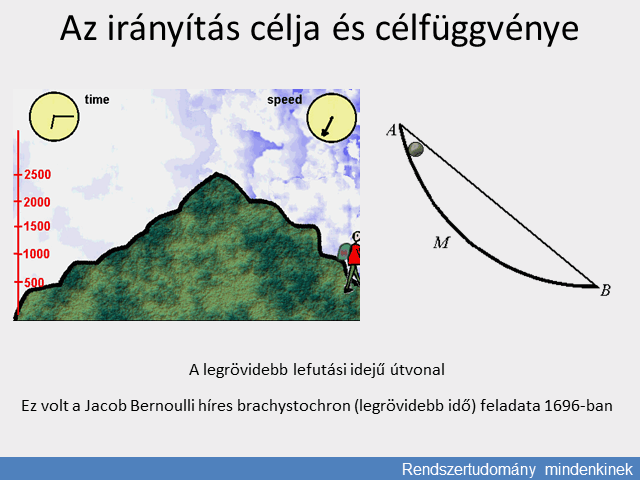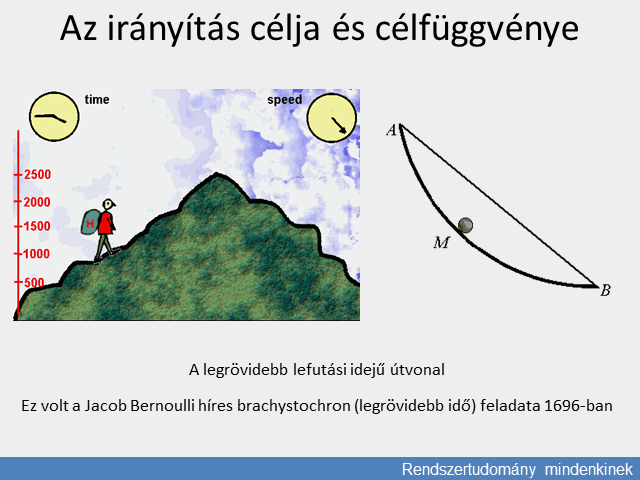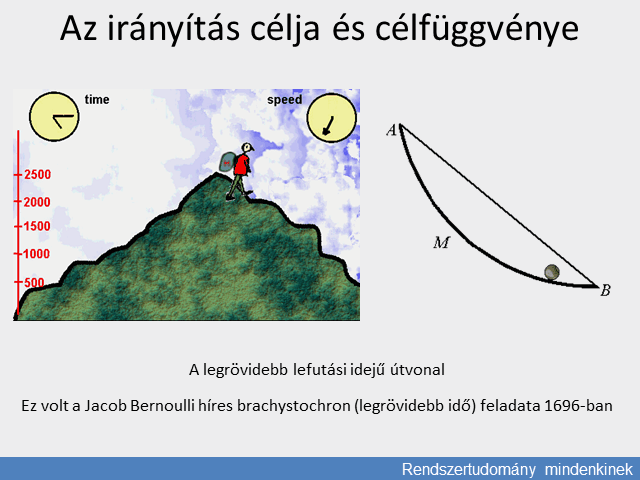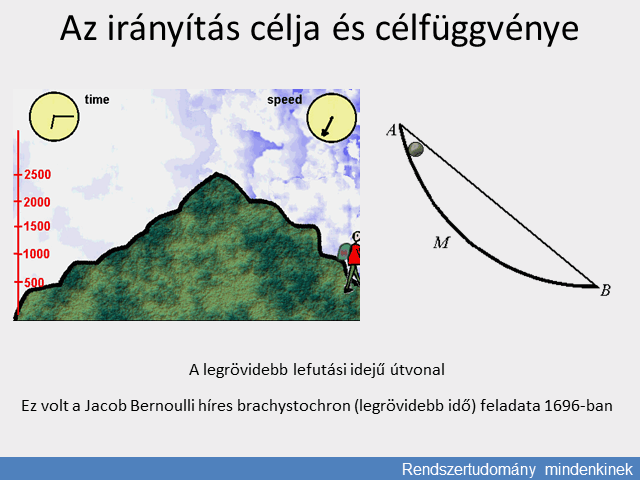
A probléma akkor lett érdekes, amikor az ember kezdett a mozgásnak is ura lenni. Így a kérdés és annak matematikai modellje a XVII. század legvégén merült fel, Johann Bernoulli feladatával, a két pont között legördülő, álló helyzetből induló legkedvezőbb mozgás, azaz a leggyorsabb útvonal keresésével, a brachystochron (legrövidebb idő) feladvánnyal. A kor legnagyobb matematikusai igyekeztek válaszolni és ebből a gondolkodásból jött létre a variációszámítás, a differenciálszámítás és a rendszerek változásának Lagrange-i energetikai modellje. A sokváltozós, bonyolult folyamatokra ezek a számítások a mozgás analógiái alapján vihetők át, lineárisként közelíthető esetekben a mátrixszámítások segítségével.
Az irányítandó folyamat modellje leírja az elérendő célhoz vezető változást és ebben kell kiválasztani a legkedvezőbb változatokat, az optimumokat.