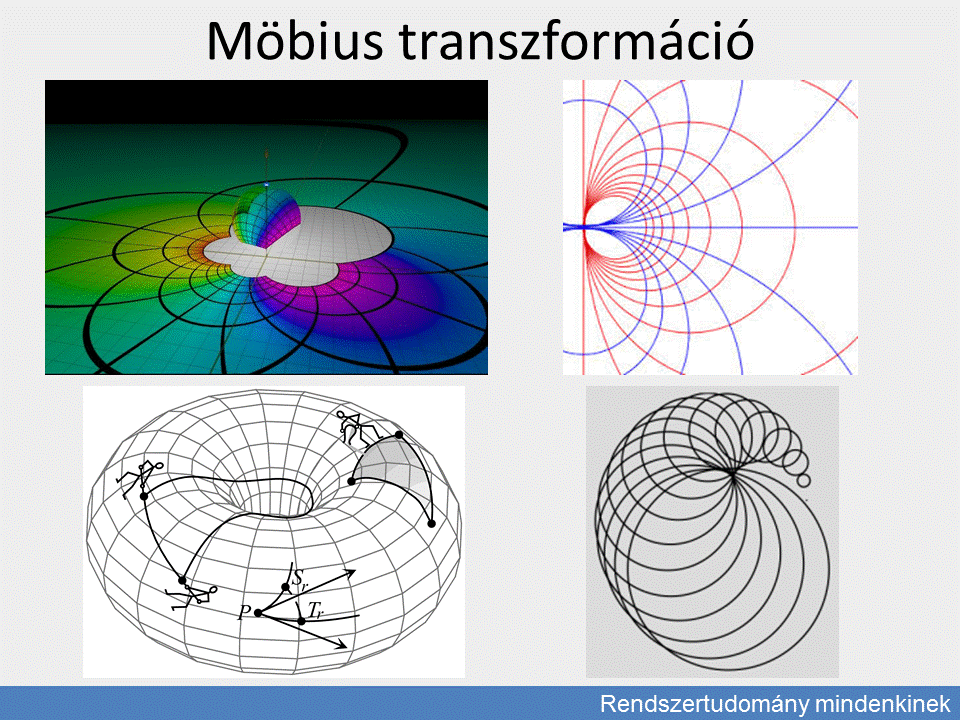

A Möbius-transzformáció
A transzformációt kitűnően mutatja a mellékelt videó.
A Möbius transzformáció az eukleidészi tér alakzatait forgatja és arányosan (lineáris mértékkel) torzítja, alkalmazásainkban a végtelenbe nyúló tereket és azokban a folyamatokat egy kör belsejébe transzformálja. Ez a kör általában egységsugarú és így azt az inverziót képezi le, amelyet a folyamat visszacsatolása hoz létre.
A transzformációt a komplex számsíkra alkalmazzuk, ahol a folyamat állapotának pontjait vektorokkal ábrázoljuk, a vektor hossza a folyamat által előidézett erősítés, vagy csillapítás mértéke, a fázisszöge pedig a folyamat bemenetének és kimenetének időeltolódását reprezentálja.
A Möbius-transzformáció a folyamatok olyan csoportjával végezhető el, amelyeket polinomokkal, a tárgyalt szakaszon mindenütt differenciálható, holomorf függvényekkel lehet leírni, azaz a gyakorlatban előforduló folytonos folyamatok széles körében használható.
A Möbius transzformáció a maga zsugorító, bővítő, forgató hatásával része minden olyan képfeldolgozó eljárásnak, amely egy probléma részleteinek és összefüggéseinek, sokoldalúságának vizsgálatát támogatja, a csoporttulajdonságok szigorúságával megőrzi a vizsgált tulajdonságokat és hitelesen visszaforgathatóvá teszi a képeket.
Ugyanilyen a jelentősége a képi reprezentációból elvonatkoztatott, matematikai-számítástechnikai eszközökkel leírt jelenségek vizsgálatában, a stabilitás és a rendszerminőség problémáiban. Ezeket a modern rendszerelméletben elsősorban a Hardy-terekben vizsgáljuk, amelyek szintén a Mőbius-transzformáció által alkotott térfogalmak.