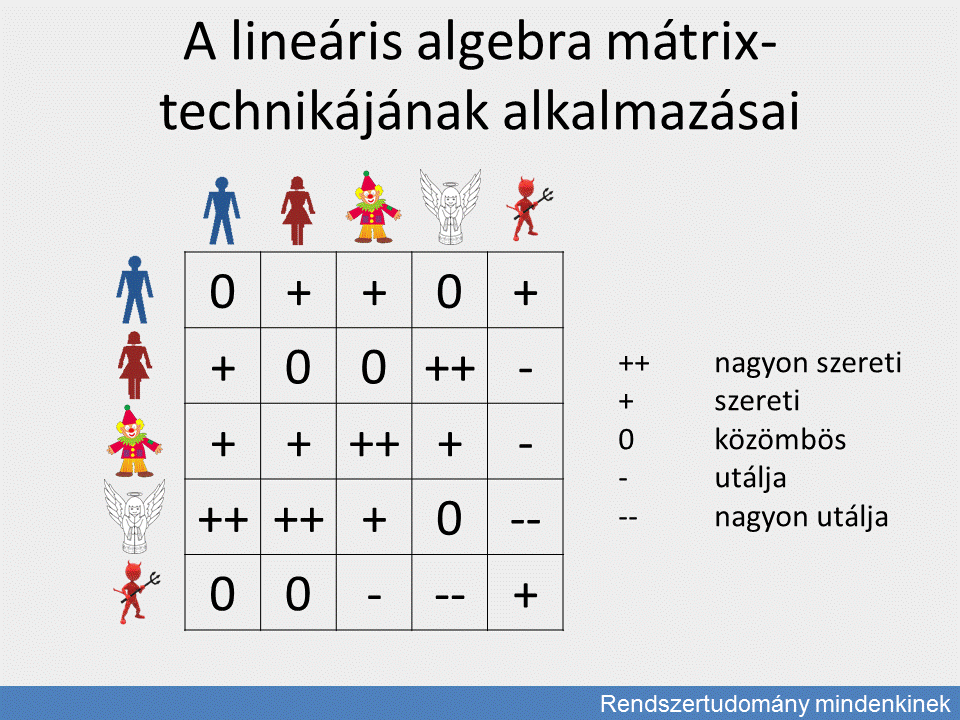

A lineáris algebra mátrix-technikájának alkalmazásai
Számítástechnikailag is fontos csoportkövetkezmény, hogy a lineáris algebra mátrix technikája kényelmes és jól kidolgozott módszerekhez vezeti a felhasználót, az összefüggések a lineáris szuperpozíció lehetőségével minden lineáris algebrai számítást lehetővé tesznek. Ebből következik az, hogy a két- és háromdimenziós módszerek jól bővíthetők sokdimenziósokra, ami a sokváltozós rendszereknek, mint sokdimenziós alakzatoknak a számítását teszi lehetővé.
A stacionáriusság alapján feltételezzük, hogy a folyamat korábbi és várható viselkedésének statisztikus jellemzői azonosak. Így a korábbi megfigyelések átvetíthetők a későbbi viselkedésre. A megfigyelhetőségnek ezt a korábbi lehetőségét tekintjük a folyamat megfigyelhetőségének feltételeként és a jövőre történő kivetítés lehetőségét a szabályozhatóságén. A múlt és jövő ilyen egymásra vetítését a Hankel-mátrixokkal írjuk le, ezek ferdén szimmetrikus transzformációk. A nemstacionárius folyamatokban a folyamatosan belépő, új jelenségeket a Toeplitz-mátrix reprezentálhatja. A jelek, jelenségek egymás közti viszonyait a Gram-mátrixokkal kezelhetjük. A Gram mátrixoknak fontos szerepük van a szabályozhatóság és a megfigyelhetőség eldöntésében.
Az egyváltozós, lineáris, stacionárius és bizonytalansági zavarások, zavarójelektől mentes alapmodell bővíthető ezen modell-feltétetelek módosításaival. Az algebra és ebben a csoportelmélet éppen ezeknek a bővítéseknek szab lehetőséget és szigorú határokat. A transzformációk is ezen lehetőség- és szabályrendszeren belül kezelendők. Így az alapmodell érvényessége bővül, ha a Hankel-mátrixba függvények kerülnek, amelyek a rendszer bemenete és kimenete közötti nemstacionárius és nemlineáris összefüggéseket reprezentálják. A korlátozások figyelembe vételét segíti azoknak az analitikus függvényeknek a használata, amelyek egyébként is a valós jelenségek menetét megközelítő reprezentációk alapmódszerei.