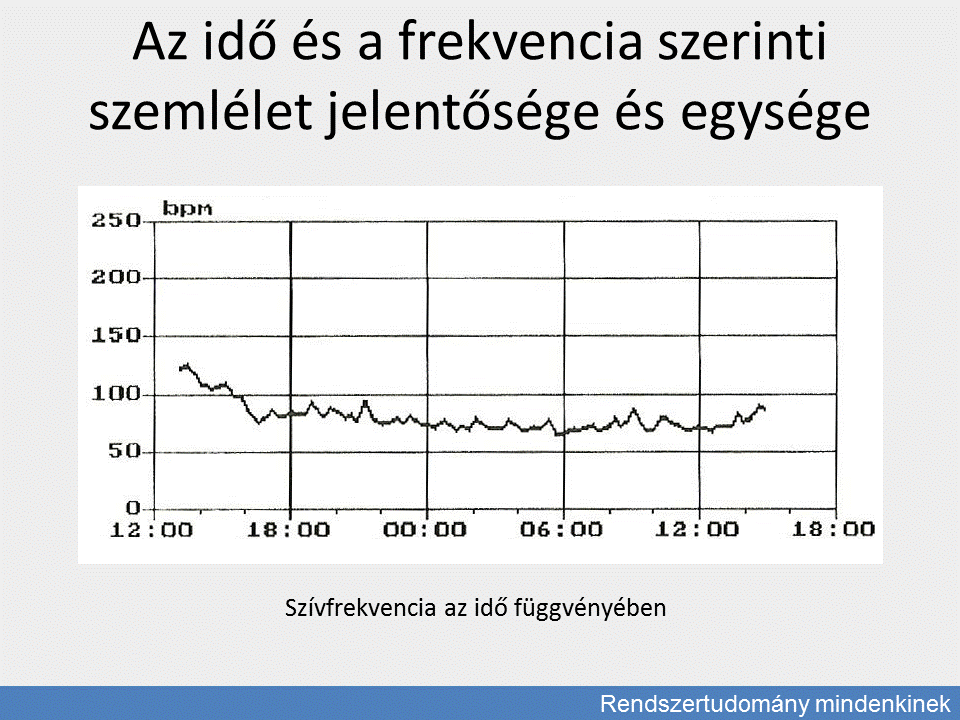

Az idő és a frekvencia szerinti szemlélet jelentősége és egysége
A csoporton belül lehetséges transzformációk nyitják meg az utat a különböző szempontú reprezentációk felé. Ezek közül a legfontosabb a polinomos, hatás-idő ábrázolások átvitele a Fourier- és Laplace-transzformációk hatás-frekvencia világába és az exponenciális és a hiperbolikus függvény-változók tartományaiba. Mind arra szolgál, hogy a folyamat viselkedését más és más szempontok szerint tudjuk szemlélni és a szemlélettel kapcsolódó ábrázolást a folyamat tervezésénél és vizsgálatánál alkalmazni.
Az idő- és a frekvenciaszemléletnek történelmileg és fizikai probléma-gyökerében is különböző eredete van. Az időben és térben szemlélt természeti folyamatok matematikai leírása volt a kiindulás.
A folyamatok, először közönséges, majd parciális differenciálegyenletekkel történő reprezentálásának hosszú útja volt a tizenhatodik század végétől Galilein és Newtonon át az inga mozgásának, majd a gravitációs és egyéb tömeghatásoknak időbeli és térbeli tanulmányozásától addig a gondolatsorig, amely elvezetett az energia és a potenciál fogalmaihoz. Ezek egyensúlyai, tartamukat megőrző tulajdonságai lettek a fizika fogalmainak matematikai reprezentációi, egész valós rendszervilágunknak számítási keretei. Ilyenek a mechanika Hamilton-i, az elektrodinamika Maxwell-i egyenletei, részben a kvantumelmélet alapösszefüggései.
A hővezetés megfigyeléséből származott Joseph Fourier elmélete, a jelenségek frekvencia-függvényekre felbontása és tovább, mindaz, ami a kétfajta, de ugyanarra a folyamatra vonatkozó reprezentáció egymásközti kapcsolatait, egymásba történő átalakításait fejlesztette ki, és ezek azok az összefüggések, amelyeket a számításainkban ma is használunk. Valamennyi hullámjelenség vizsgálata ezzel a reprezentációval dolgozik, a mai fizikai valóságban az anyag, a fény, az energia kettős természete ebben a kettős reprezentációban egyesül. A holografikus kép ennek szemléltetője, ugyanazon képet digitális eszközeinkkel időben soros módon adjuk át, a holográfiában viszont, a megnevezés értelme szerint is, a teljes kép közvetítődik, annak adott frekvenciatartománybeli megközelítéseként.
A csoportelmélet szép példája a két szemlélet matematikájának bijektív transzformációja, az időfüggvény differenciálegyenletek Taylor-sorainak és a Fourier-soroknak egymásnak történő megfeleltetései. Ebben a használatban ez a reprezentációs eszközrendszerünk, amivel gyakorlati rendszertudományi, szabályozási problémáinkat kezeljük.