

Predikciós szabályozás
A predikciós irányítás gondolata az 1970-es években merült fel. Először ipari alkalmazásai voltak, elméletileg azután vizsgálták a tulajdonságait. Az algoritmus az eredeti változatában egyszerű, az ipari gyakorlatban is mérhető modelleket használ (például a folyamat mérhető ugrásválaszát). A cél robusztus irányítás tervezése, amely elfogadható viselkedést ad akkor is, ha a folyamatban korlátozások, zajok és paraméter bizonytalanságok fordulnak elő.
Az alapgondolat a következő. A folyamat modellje alapján prediktáljuk, előre számítjuk a jövő egy adott tartományában a kimenőjel várható alakulását. A jövőbeni alapjelet ismertnek tekintjük az adott tartományban. Egy négyzetes költségfüggvényt adunk meg, amely tekinti a jövőbeni alapjel és kimenőjel négyzetes eltérését az adott időtartományban "horizonton", és a bemenőjel növekményeket is figyelembe veszi. A költségfüggvényt minimalizálva megkapjuk a beavatkozójel sorozatot, amelyből azonban ténylegesen csak az első értéket adjuk a folyamat bemenetére, majd a következő mintavételi pontban az eljárást megismételjük (csúsztatott horizontú technika).
A költségfüggvényt az alábbi összefüggéssel adjuk meg:
$J=\sum\limits_{n_e=n_{e1}}^{n_{e2}}$ $ \lambda_{{yn}_{e}} \left[y_{r} \left(k+d+n_{e} +1\right)-\hat{y}(k+d+n_{e} +1|k)\right]^{2} $ $+\sum\limits_{j=1}^{n_{u} }\lambda _{{\rm uj}} \Delta u^{2} \left(k+j-1\right)$; $\Rightarrow \min\limits_{\Delta u}$
A költségfüggvény első tagja a referenciajel és a prediktált kimenőjel eltérését tekinti a predikciós horizonton, míg a második tagja a nagy beavatkozójel növekményeket bünteti.
$k$ az aktuális időpont, $d$ a diszkrét holtidő, ami a fizikai holtidő és a mintavételezési idő hányadosa (egész szám). Az előrejelzést még egy további $n_{{\rm e}} +1$ lépéssel előreszámítva kezdjük.
A szabályozás hangoló paraméterei a predikciós tartomány, amely a végső $n_{{\rm e}2} $ és a kezdeti $n_{{\rm e}1} $ pontok különbségével adható meg, az $n_{{\rm u}} $ szabályozási tartomány, amely megadja, hogy az optimalizálásnál hány egymást követő beavatkozó hatást veszünk figyelembe. A $\lambda$ paraméterek súlyozó tényezők.
A minimalizáláskor a korlátozások is figyelembe vehetők. Numerikus optimalizálási eljárások alkalmazhatók.
A szabályozás elvét az 1. ábra szemlélteti.
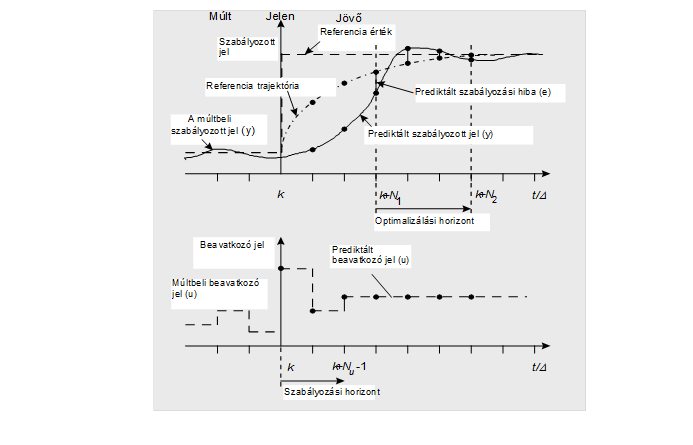
1. ábra A predikciós szabályozás elve
Ha a folyamatmodell lineáris és nincsenek korlátozások, analitikus megoldás adható.
Lineáris esetben a prediktált kimenőjel felbontható szabad és gerjesztett válasz összegére.
$y=y_{{\rm szabad}} +y_{{\rm gerjesztett}} $
A szabad válasz a múltbeli beavatkozójelek vagy beavatkozó jel növekmények hatása a jövőbeni kimenőjel lefolyására, a gerjesztett válasz pedig az aktuális és a jövőbeni beavatkozójelek hatása a jövőbeni kimenőjelre. A múltbeli beavatkozások hatása a jövőbeni kimenőjelre nem változtatható meg, azt a rendszernek el kell viselnie. Viszont az aktuális és jövőbeni beavatkozó jelek vagy azok növekményei optimalizálhatók a költségfüggvény minimalizálásával. A csúsztatott horizontú technika igen hatásos elv, mivel ezzel a szabályozás alkalmazkodni tud a változó körülményekhez (zavarások, paraméter bizonytalanságok, stb.).
Az alábbi JAVA applet szemlélteti egy elsőrendű rendszer esetében, hogy a jövőbeni kimenet a szabad és a gerjesztett válaszból tevődik össze. Továbbá szemlélteti a predikciós szabályozás működését is.
A predikciós szabályozási algoritmusokkal a szabályozás jobb minőségi viselkedése érhető el, mint a szokásos PID algoritmusokkal, különösen ha a referenciajel előre ismert és a folyamat holtideje nagy. Több információ alapján, a várható viselkedést előre látva jobb döntéseket hozhatunk, mintha csupán az aktuális időpontban tekintjük az alapjel és a kimenőjel eltérését és ennek alapján határozzuk meg a beavatkozójelet. Mivel a szabályozás előre látja a holtidő utáni viselkedést, a beavatkozó hatás már a változások bekövetkezése előtt fellép azok hatásának követésére illetve elhárítására.
Manapság állítható, hogy az ipari szabályozásoknál a PID szabályozási algoritmusok mellett a predikciós szabályozások a másodsorban leginkább alkalmazott algoritmusok.
A folyamat modellnek predikciós modellnek kell lennie, amely a jövőbeni jel számításához a bemenőjelről és a kimenőjelről csak az aktuális és a korábbi értékeket használja fel. A még nem ismert jövőbeni jelértékeket a predikció során nem használhatjuk fel. Vannak ún. predikciós folyamatmodellek (pl. a súlyfüggvény vagy az átmeneti függvény). Ha a modell nem predikciós, akkor predikciós átalakítást kell végezni a predikciós algoritmus alkalmazása előtt.
A predikciós algoritmusok különböző változatait adták meg attól függően, hogy a modell lineáris vagy nemlineáris, illetve milyen a folyamatmodell és hogyan adjuk meg a zajmodellt.
A nagy cégek, mint pl. a Shell vagy a Honeywell, olyan folyamatirányítási szoftvereket dolgoztak ki, amelyek alkalmasak az ipari folyamat identifikációjára a folyamatra adott alkalmas vizsgálójelekkel és azok hatásának elemzésével, illetve megtervezik a szabályozót és a beavatkozójelet valós időben alkalmazzák a folyamat bemenetén. Ezek a szoftverek a szabályozási algoritmusok között a predikciós szabályozás tervezését is támogatják.
Hivatkozások
Richalet, J., A. Rault, J.L. Testud, J. Papon (1978). Model-predictive heuristic control: Applications to industrial processes. Automatica, Vol.14, pp. 413-428.
Cutler, C. R., B.L. Ramaker (1980). Dynamic matrix control - a computer control algorithm. Joint Automatic Control Conference, Prepr. Vol.1. Paper WP5-B, San Francisco.
Clarke, D.W., C. Mohtadi, P.S. Tuffs (1987). Generalized predictive control – Part I. The basic algorithm. Automatica, Vol. 24, 2, 137-148.
Camacho, E.F., Bordons, A.C. (2014) Model Predictive Control. Springer.
Haber, R., Bars, R., Schmitz, U. (2011). Predictive Control in the Process Engineering. From the Basics to the Applications, Wiley.
