

PID szabályozási algoritmus
Egy szabályozási körnek megadott minőségi előírásokat kell teljesítenie. Ezek az előírások az irányítási céloktól, az adott folyamat technológiájától és magától a folyamattól is függnek. Vizsgálni kell a szabályozás viselkedését, illetve úgy kell megterveznünk a szabályozást, hogy az eleget tegyen a minőségi követelményeknek. Az irányítással a rendszer elindítását, megfelelő üzemben tartását (kimenőjeleivel a megadott alapjelek követését, a zavarások elhárítását), majd megfelelő leállítását kívánjuk biztosítani.
Az indítást, leállítást általában logikai feltételek figyelembe vételével, nyílt hurokban vezéreljük. Az indítási, leállítási folyamat általában nem függ a folyamat kimenőjelétől.
A folyamat megfelelő üzemben tartását általában zárt hurkú szabályozással biztosítjuk, amely az alapjel és a mért kimenőjel különbsége alapján avatkozik be a folyamat bemenőjelébe. Az alapkapcsolás a negatívan visszacsatolt soros szabályozási struktúra, amelyben a szabályozó sorosan kapcsolódik a folyamathoz (1. ábra).
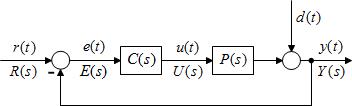
1. ábra Szabályozási kör
Egy folyamat irányításakor a vezérléseknek és a szabályozásnak összehangoltan kell működniük. A negatív visszacsatoláson alapuló szabályozás kiegészíthető olyan strukturális elemekkel, amelyek segítségével javíthatók a zavarelhárítási tulajdonságok.
A szabályozási körben az alapjel és a mért kimenőjel különbsége adja a szabályozó bemenőjelét, amelynek kimenőjele működteti a beavatkozó berendezést, amely a folyamat bemenőjelét adja. A szabályozót úgy kell megtervezni, hogy a folyamat teljesíteni tudja a szabályozással szemben támasztott minőségi követelményeket. A szabályozót a folyamat modelljéhez és a minőségi előírásokhoz tervezzük.
Az ipari gyakorlatban a legelterjedtebbek az ún. PID szabályozások, amelyek a hibajellel arányos, a hibajelet integráló, illetve a hibajel változási meredekségéből képzett jeleket súlyozottan összegezve adják a beavatkozójelet. A szabályozó a folyamat bemeneti-kimeneti modelljét veszi alapul.
Az állapotmodellel leírt rendszerhez tervezhetünk az állapotváltozók visszacsatolásán alapuló szabályozást, ahol az állapotokat visszacsatoló konstansok számíthatók a zárt rendszer pólusainak megfelelő, kívánt elhelyezéséből, vagy egy minőségi kritérium optimalizálásából.
A valóságos rendszerekben korlátozások lépnek fel, ha a bemenőjel meghalad egy adott értéket. A korlátozás bekövetkezése kedvezőtlen jelenségekkel járhat. A korlátozások kezelésére különböző módszerek vannak.
A legtöbb folyamat nemlineáris. Általános, jól kidolgozott vizsgálati és tervezési (analízis és szintézis) módszerek lineáris rendszerekre állnak rendelkezésre. A nemlineáris rendszereket egyedileg kell vizsgálni. Sokszor a nemlineáris rendszert a munkapontok környezetében kis változásokra szakaszonként linearizáljuk, és a linearizált rendszerhez tervezünk szabályozót.
PID szabályozási algoritmusok
Az alábbiakban a PID szabályozási algoritmusokat tárgyaljuk kissé részletesebben. A szabályozó párhuzamosan kapcsolt proporcionális, integráló és differenciáló hatást tartalmaz, ezzel reflektál a hibajel aktuális értékére, a múltbeli lefolyására és a jövőbeni változási trendjére (2. ábra).
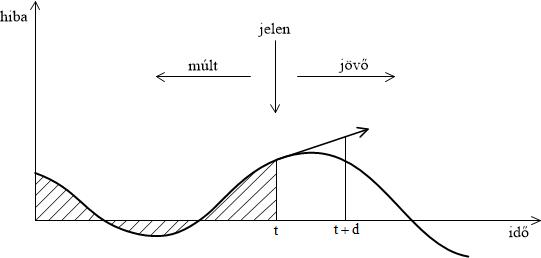
2. ábra A PID szabályozó a hibajel aktuális értékét, múltbeli értékét és jövőbeli trendjét is figyelembe veszi (Åström nyomán)
Az ideális PID szabályozó a beavatkozójelet a hibajelből az alábbi összefüggéssel képezi:
$u\left(t\right)=k_{c} e\left(t\right)+k_{I} \int _{0}^{t}e\left(\tau \right) d\tau +k_{D} \frac{de\left(t\right)}{dt} , $
A szabályozó átviteli függvénye:
$C_{PID} \left(s\right)=k_{c} \left(1+\frac{1}{sT_{I} } +sT_{D} \right)$
Az ideális differenciáló hatás azonban nem realizálható (a deriválás pl. egységugrás bemenet esetén végtelen impulzust eredményezne, ami a gyakorlatban nem megvalósítható). Ezért a reális PID szabályozóban a differenciáló hatás mindig egy energiatárolós késleltetéssel együtt jelenik meg. A reális PID szabályozó átviteli függvénye:
$C_{PID} \left(s\right)=k_{c} \left(1+\frac{1}{sT_{I} } +\frac{sT_{D} }{1+sT_{1} } \right)$
Ha az algoritmusban csak a proporcionális hatást használjuk fel, P szabályozóról beszélünk. Ha a proporcionális és integráló hatást alkalmazzuk, PI szabályozóról, ha a proporcionális és differenciáló hatást vesszük, PD szabályozóról, ha pedig mindhárom hatást alkalmazzuk, PID szabályozóról beszélünk. Az integráló hatás növeli a szabályozás statikus pontosságát az alapjelkövetésre és a zavarelhárításra. A differenciáló hatással gyorsítani tudjuk a rendszert.
A PID szabályozó átviteli függvényét közelíthetjük a következő alakban:
$C_{PIDappr} \left(s\right)=k_{c} \left(\frac{1+sT_I}{sT_{I} }\cdot \frac{1+s\tau }{1+sT_{1} } \right)$
ahol $\tau = T_D+T_1>T_1$. Ha $T_I>\tau>T_1$ jó közelítést kapunk. Ezzel a reális PID szabályozó sorosan kapcsolt PI és PD szabályozóként adható meg.
A PID jellegű szabályozók könnyen megvalósíthatók analóg integrált műveleti erősítőkkel (3. ábra). Az erősítő bemenetére és visszacsatolásába iktatott impedanciák jellegével állítható be a szabályozó típusa.
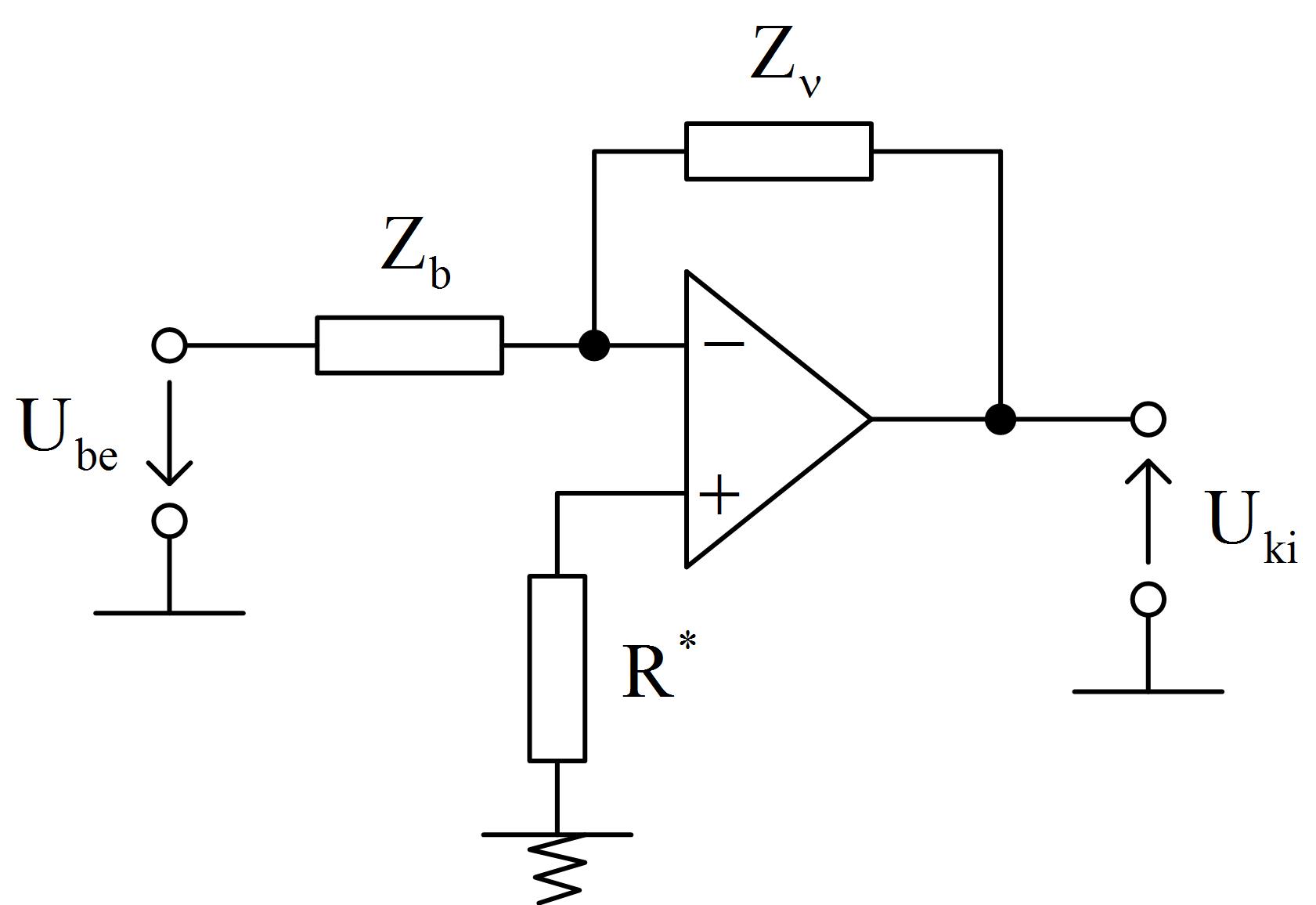
3. ábra A PID szabályozók megvalósíthatók analóg integrált műveleti erősítővel

4. ábra PID szabályozó egységugrás válasza
A kezdeti túlvezérlés a differenciáló részből adódik, ez gyorsítja a szabályozási rendszert, míg a nagy időkre az integráló hatás lesz a domináns, ez biztosítja a statikus pontosság növelését.
Természetesen a túlvezérlést a szabályozónak, illetve a beavatkozószervnek el kell tudnia viselni (például egy szelepnek hiába adunk arra parancsot, hogy a maximális átfolyó mennyiségnél nagyobbat biztosítson, az csak a maximális értékét tudja kiadni.)
Az 5. ábra szemlélteti, hogy egy PD szabályozó azáltal gyorsítja a rendszert, hogy a kezdeti túlvezérlést a rendszer úgy tekinti, mintha a saját időállandójával egy sokkal nagyobb értéket kellene elérnie, majd mikor a beavatkozójel lecsökken, a kimenőjel már majdnem elérte az állandósult értékét.

5. ábra A PD hatás gyorsítja a rendszert
A PID szabályozónak 4 paramétere van, ezek a erősítés, a integrálási időállandó, a differenciálási időállandó és a energiatárolós időállandó. Ezeket a paramétereket úgy kell hangolni az adott rendszerhez, hogy a zárt rendszer teljesítse a minőségi előírásokat. Először is el kell dönteni, hogy a PID jellegű szabályozók közül melyiket választjuk (P, PI, PD vagy PID). Azután a paramétereket kell megfelelően hangolni. Ez történhet ún. ökölszabályok alapján: a folyamatot identifikáljuk például egy energiatárolós holtidős tagként és ehhez táblázat alapján választjuk meg a szabályozó paramétereit. A hangolás történhet a nyitott kör amplitúdó-frekvencia diagramjának megfelelő formálása alapján is. Egy szokásos hangolási technika a póluskiejtés, amikor is a folyamat kedvezőtlen pólusait a szabályozó zérusaival „kiejtjük”, és a kedvezőtlen pólusokat kedvezőbbekkel helyettesítjük. Például a PI hatással kiejtjük a folyamat legnagyobb időállandóját és behozunk helyette egy integráló hatást. A közelítő PID szabályozó hangolásakor a PI tényezővel kiejthetjük a folyamat legnagyobb időállandóját és behozunk helyette egy integráló hatást, a PD tényezővel pedig kiejthetjük a folyamat következő legnagyobb időállandóját, és behozunk helyette egy jóval kisebb időállandót. Az erősítést úgy választjuk meg, hogy a szabályozás stabilis maradjon és legyen elegendő fázistöbblete (pl. legyen a fázistöbblet 60°, vagy annál nagyobb). A PD hatással kiejtjük a második legnagyobb időállandót, és behozunk helyette egy kisebb időállandót. A hangoláskor figyelembe vehetjük a folyamat modelljében meglévő bizonytalanságokat és ún. robusztus szabályozás tervezésére törekszünk, amikor a szabályozás még kielégítően működik akkor is, ha a megadott tartományba eső paraméterbizonytalanságok lépnek fel. A hangolásnál törekedhetünk a hibajel valamilyen (négyzetes, idővel súlyozott abszolútérték) integráljának minimalizálására is.
Az ipari gyakorlatban azért terjedtek el a PID szabályozások, mert a P, I és D hatásokkal rendszerint valamennyi minőségi követelmény kielégíthető, és gyakorlati megvalósításuk egyszerű és árban is mérsékelt volt az analóg integrált műveleti erősítők alkalmazásával.
Az alábbi Java applet szemlélteti a folytonos párhuzamos PID szabályozás működését. A folyamat és a szabályozó átviteli függvényei megadhatók, és megjeleníthető a szabályozás kimenőjele és beavatkozójele egységugrás alapjel és zavarások hatására.
Az alábbi Java applet szemlélteti a folytonos soros PID szabályozás működését. A folyamat és a szabályozó átviteli függvényei megadhatók, és megjeleníthető a szabályozás kimenőjele és beavatkozójele egységugrás alapjel és zavarások hatására.
Napjaink gyakorlatára egyre növekvőbb mértékben jellemző, hogy az irányítási rendszereket megfelelő valós idejű (real-time) szolgáltatásokkal is rendelkező digitális berendezések valósítják meg. Attól függően, hogy egy adott alkalmazáson belül hány és milyen bonyolultságú szabályozási kör feladatát kell ellátni, a digitális irányító berendezések köre az egyetlen chip-ből álló mikrokontrollerektől a nagyobb teljesítményű midi/mini gépekig terjed. A digitális berendezések hálózatba szervezésének fejlettsége lehetővé teszi elosztott irányítási rendszerek létrehozását is.
A szabályozási funkció digitális megoldása az iparban alkalmazott irányítástechnikai kultúrát is jellemzi. Nevezetesen arról van szó, hogy a gyakorlati irányítástechnika a különböző vezérlési és szabályozási feladatok kombinációinak egységes – kézenfekvően digitális rendszerű - megvalósítását igényli.
Zárt mintavételes szabályozási körök alapvető elvi felépítését a 6. ábra szemlélteti. A szabályozott szakasszal kapcsolatban - az ábrából is láthatóan – azzal a feltételezéssel élünk, hogy az egy folytonos folyamat. A folytonos folyamat időben folytonos bemenőjelével és kimenőjelével ellentétben a digitális irányító rendszer működése diszkrét idejű, hiszen a folyamatirányítást megvalósító program adott működtetési frekvenciával működő CPU vezérelte irányító berendezésen fut. A folytonos folyamat analóg jellegű és az irányító berendezés digitális jellegű jelfelületét illeszteni kell egymáshoz, ezt a feladatot a zárt szabályozási körbe beiktatott átalakító szervek látják el. A tartószerv alapfeladata diszkrét jelsorozatból folytonos bemenőjel előállítása. Az elnevezéseket illetően analóg - digitális irányban mintavevő szervről, digitális - analóg irányban tartószervről beszélünk. A mintavevő szerv gyakorlatilag minden esetben egy a digitális technikából jól ismert A/D (Analog to Digital) átalakító, a tartószerv – tipikusan, de nem feltétlenül - D/A (Digital to Analog) átalakító. A mintavevő és tartószervek működését, a digitális berendezés központi egységét, lényegében a rendszer szinkronizálását, közös rendszeróra vezérli. A zárt szabályozási rendszerben folytonos és diszkrét idejű jelek is szerepelnek, továbbá ugyanazon jelről analóg és digitális információ is állhat rendelkezésre.
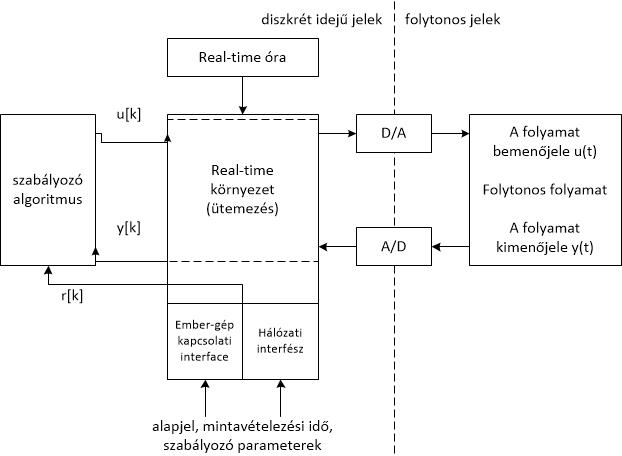
6. ábra Mintavételes szabályozási kör felépítése
A diszkrét szabályozó algoritmus gyakran a PID folytonos szabályozó diszkretizált változata, egy program, amely minden mintavételi lépésben előállítja az aktuális beavatkozójelet. Természetesen más diszkrét szabályozási algoritmusok is programozhatók.
A diszkrét algoritmus azonban lehet más algoritmus is. A PID szabályozó mellett az iparban leggyakrabban alkalmazott algoritmus a predikciós szabályozó, amelynek alapelvét az alábbiakban ismertetjük.
A folyamatot impulzusátviteli függvényével adjuk meg, ami a mintavételezett kimenőjel és a mintavételezett bemenőjel z-transzformáltjainak hányadosa. (A folyamat bemenetén zérusrendű tartószervet feltételezünk.) (lásd az 53. oktatási oldalt.)
A folytonos rendszer átviteli függvényének pólusai és a mintavételezett rendszer impulzusátviteli függvényének pólusai között exponenciális összefüggés adja meg a leképezést.
Ha például egy háromtárolós arányos folyamatot tekintünk, annak átviteli függvénye:
$P(s)=\frac{1}{(1+sT_1)(1+sT_2)(1+sT_3)}$
és impulzusátviteli függvényének alakja $T_s$ mintavételezési idő mellett
$G(z)=\frac{Y(z)}{U(z)}=\frac{\delta(z+\sigma_{1})(z+\sigma_{2})}{(z-e^{-T_s/T_1})(z-e^{-T_s/T_2})(z-e^{-T_s/T_3})}$
A póluskiejtési stratégiával a diszkrét PID szabályozó $C(z)$ impulzusátviteli függvényének alakja:
$C(z)=\frac{k_c(z-e^{-T_s/T_1})(z-e^{-T_s/T_2})}{(z-1)(z-e^{-T_s/T_{2a}})}$
ahol a szabályozó PI tényezője „kiejti” a folyamat legnagyobb $T_1$ időállandójából adódó pólust és „behoz” helyette egy integráló hatást, és PD tényezője pedig kiejti a következő legnagyobb $T_2$ időállandóját és behoz helyette egy kisebb $T_{2a}$ időállandót. Ez az időállandó a diszkrét esetben lehet 0 is, ebben az esetben ideális PID szabályozásról (kompenzációról) beszélünk.
A folytonos és a diszkrét PID kompenzációra a Példa ablakban tervezési példát mutatunk be.
