
Szabályozási struktúrák
Körülöttünk mindenütt rendszerek vannak. A rendszerek kimeneteit, állapotait irányítani kell, hogy eleget tegyenek a minőségi előírásoknak. A szabályozott kimenőjeleknek követniük kell az alapjel változásait a rendszerre ható zavarások ellenére, miközben nem léphetik túl a technológiából adódó korlátokat.
A szabályozás alapstruktúrája a negatív visszacsatolás
A szabályozási rendszerek a negatív visszacsatoláson alapulnak. Az y kimenőjelet érzékeljük az érzékelőszervvel, a mért jelet összehasonlítjuk az alapjellel, amit az alapjelképzőszerv állít elő. Az e különbségi jel, a hibajel működteti a C szabályozót, amelynek kimenőjele a beavatkozószerven keresztül képezi a P folyamat u bemenőjelét. A szabályozási struktúrát az 1. ábra mutatja. Sokszor az alapjelet szűrjük az F szűrőtagon keresztül.
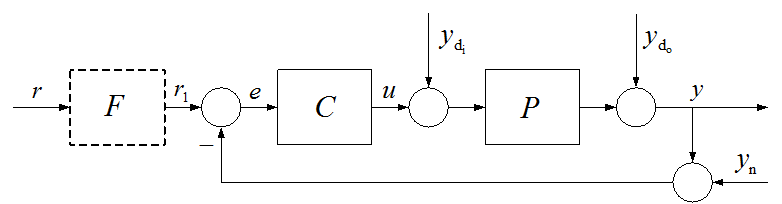
- ábra Zárt szabályozási kör
A C szabályozót úgy kell megtervezni, hogy a szabályozás eleget tegyen a minőségi előírásoknak, legyen stabilis, kövesse az alapjelet, küszöbölje ki a kimeneti és bemeneti zavarások hatását a kimenőjelben, csökkentse a mérési zaj hatását, legyen érzéketlen a folyamat paramétereinek változására, miközben az előírt korlátokat nem haladja meg.
Ha a változás hatása megjelenik a kimenőjelben, a szabályozás fellép a hatás kiküszöbölésére. Például, ha a bemeneten zavarás lép fel, egy idő után ez befolyásolja, megváltoztatja a kimenőjelet, megváltozik a hibajel is, ami a beavatkozójel módosításával a folyamat kimenőjelét az eredeti értéke felé mozdítja el. Ehhez azonban a folyamat tehetetlensége miatt időre van szükség. A negatív visszacsatolás alapvető tulajdonságait korábban tárgyaltuk.
Ha a kimenőjelen kívül más jelek is mérhetők (zavarások vagy belső állapotváltozók) ezek a további információk az alap szabályozási struktúra módosításával felhasználhatók a szabályozás működésének javítására. Több elérhető információ alapján körültekintőbb, jobb döntéseket hozhatunk.
A szabályozás zavarelhárítási képességének növelése
Ha a folyamat tehetetlensége nagy, nagyok az időállandói, hosszabb időbe telik, hogy a zavarás hatása mutatkozik a kimeneten és a szabályozás fellép a zavarás hatásának kiküszöbölésére. Különösen a bemeneten ható zavarás hatásának kiküszöbölése lehet lassú.
Ha a folyamat zavarójele vagy valamilyen közbenső jele mérhető, akkor e járulékos információk felhasználásával a szabályozás tulajdonságai javíthatók.
Zavarkompenzáció
Ha a zavarás mérhető, a zavarásról történő előrecsatolással a szabályozás minősége, zavarelhárítási tulajdonságai lényegesen javíthatók. A zavarás mért értéke alapján már azelőtt intézkedni lehet a zavarás elhárítására, mielőtt a zavarás hatása a kimenőjelben megmutatkozna. A zavarkompenzációval kiegészített szabályozás hatásvázlatát a 2. ábra mutatja.

2. ábra Zavarkompenzációval kiegészített szabályozási kör
A zavarás két úton hat a kimenőjelre. Az előrevezető ágban lévő $C_{{\rm n}} \left(s\right)$ zavarkompenzációs szabályozóval a zavarás hatása jelentősen csökkenthető, esetleg teljesen meg is szüntethető. A kimenőjelnek a zavarásra vonatkozó eredő átviteli függvénye:
$\frac{Y\left(s\right)}{Y_{{\rm n}} \left(s\right)} =\frac{P_{{\rm n}} \left(s\right)+C_{{\rm n}} \left(s\right)P\left(s\right)}{1+C\left(s\right)P\left(s\right)} $
Ha a kifejezés számlálója zérus, a zavarás hatása egyáltalán nem mutatkozik a kimenőjelben:
$P_{{\rm n}} \left(s\right)+C_{{\rm n}} \left(s\right)P\left(s\right)=0 $
ahonnan a zavarkompenzációs szabályozó átviteli függvénye:
$C_{{\rm n}} \left(s\right)=-\frac{P_{{\rm n}} \left(s\right)}{P\left(s\right)} .$
Amennyiben ez az átviteli függvény realizálható (számlálója nem magasabbfokú a nevezőjénél, továbbá P(s) nem tartalmaz holtidőt), a zavarkompenzáció tökéletes, a zavarás hatása a kimenőjelben egyáltalán nem mutatkozik. Ha $C_{{\rm n}} \left(s\right)$ nem realizálható, átviteli függvényét közelítjük az azt valamilyen értelemben legjobban közelítő realizálható szabályozóval.
A zavarkompenzációs beavatkozás nyílt hatásláncú vezérléssel egészíti ki a szabályozást. A zavarkompenzáció eredményessége attól függ, hogy milyen pontosan ismert a zavaró jellemzőnek a szabályozott jellemzőre gyakorolt hatása, és a rendelkezésre álló beavatkozási lehetőséggel mennyire lehet azt kompenzálni.
Kaszkád szabályozás
A szabályozott szakaszok sokszor több sorbakapcsolt részre bonthatók, és a kimenőjelen kívül a közbenső jelek is mérhetők. A 3. ábra két sorbakapcsolt részből álló folyamat hatásvázlatát mutatja. A zavaró jellemzők hathatnak a kimeneten, illetve a szakasz két tagja között. Feltételezzük, hogy maguk a zavarások nem mérhetők.
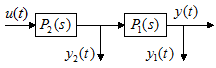
3. ábra Két sorbakapcsolt tagra bontható szakasz
A szokásos visszacsatolásos szabályozás akkor lép fel a zavarás hatásának kiküszöbölésére, ha az már a kimenőjelben megjelent. Ha a szakasz második része tartalmazza a nagy időállandókat, a zavarelhárítás lassú lesz. Ilyenkor célszerű a folyamat belső jeléről is létrehozni egy belső visszacsatolást a 4. ábra szerint. Ezt a kapcsolást nevezzük kaszkád szabályozásnak.
Mivel a belső zavarás hatása gyorsabban mutatkozik a belső jelben, mint a folyamat kimenőjelében, gyors zavarelhárítás biztosítható a $C_{{\rm 2}} \left(s\right)$ szabályozó megfelelő megtervezésével.
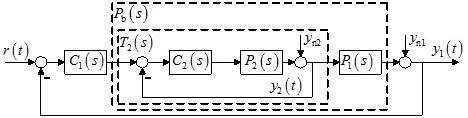
4. ábra Kaszkád szabályozás hatásvázlata
A külső szabályozási kör a $C_{{\rm 1}} \left(s\right)$ szabályozó megfelelő megtervezésével biztosítja a jó alapjelkövetést és a külső zavarás elhárítását.
Egyes alkalmazásokban a külső szabályozó után telítődő, korlátozó elemet iktatnak be. Mivel a külső szabályozó kimenőjele szolgáltatja a belső kör alapjelét, ez korlátozza az $y_{2} $ belső jel értékét, amely ily módon előírt korlátok között tartható.
Ha a folyamat több sorbakapcsolt szakaszra bontható, amelyek kimenőjelei mérhetők, több egymásba illesztett kaszkád kör is kialakítható.
Kaszkád szabályozást alkalmaznak általában villamos hajtások fordulatszám- vagy pozíciószabályozásában, ahol a kimenőjel a fordulatszám vagy a pozíció, a belső változó pedig a motor árama. A kaszkád szabályozás célja, hogy a fordulatszám tartása mellett az áram értéke ne “szaladjon meg”. Ugyanis a motor indításakor, fékezésekor vagy leterhelésekor igen nagy áramértékek léphetnek fel, miközben a fordulatszám változása lassú.
A szabályozás struktúrájának megválasztása után a szabályozó(k) paramétereit kell megfelelően hangolni, hogy a szabályozás az előírt követelményeknek eleget tegyen.
A belső modellen alapuló szabályozás (Internal Model Control, IMC)
A belső modellen alapuló szabályozás elvét Morari és Garcia vezették be. Ez a struktúra egyszerű és hatásos szabályozási kör kialakítását és tervezését teszi lehetővé. A K(s) szabályozót nyitott hurokban tervezzük a lehető legjobb alapjelkövetés biztosítására (5. ábra), majd a kört zárjuk a rendszer modelljén keresztül a 6. ábra szerint.
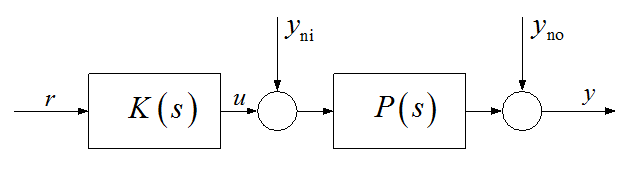
5. ábra. A K(s) szabályozót nyitott hurokban tervezzük
Az alapjelkövetés ideális lenne, ha a szabályozó a folyamat átviteli függvényének inverzét valósítaná meg. Az ideális inverz sokszor nem realizálható, ilyenkor annak legjobb realizálható közelítését alkalmazhatjuk.
A nyitott hurkú struktúrában a zavarások hatása megjelenik a kimeneten, azokat nem tudjuk kiküszöbölni. A zavarások elhárítása a folyamat belső modellen keresztül történő visszacsatolásával érhető el. A folyamat kimenőjelét összehasonlítjuk $\hat{P}$ modelljének kimenőjelével és a különbséget összehasonlítjuk az alapjellel. Ha nincsenek zavarások és a folyamat és modellje azonos, nincs visszacsatoló jel, és az előrevezető ág határozza meg az alapjelkövetés tulajdonságait. Ha van zavarás, vagy a folyamat és modellje illesztetlen, a visszacsatolás aktívvá válik, és biztosítani fogja a zavarások hatásának kiküszöbölését.
A 7. ábra a 6. ábra átalakításával kapott egyenértékű struktúrát mutat. Itt a soros szabályozó átviteli függvénye:
$C\left(s\right)=\frac{K\left(s\right)}{1-K\left(s\right)\hat{P}\left(s\right)} $
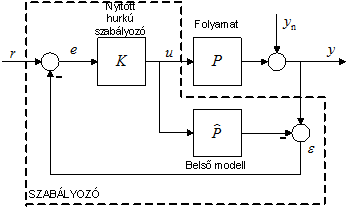
6. ábra Belső modellen alapuló szabályozás, Internal Model Control (IMC)
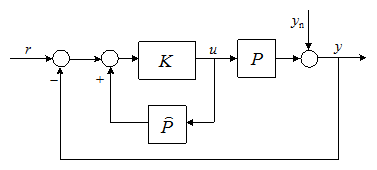
7. ábra Egyenértékű IMC struktúra
Az IMC struktúrában tehát a szabályozót nyitott körben tervezzük és a kört a folyamat modelljén keresztül zárjuk.
Állapotvisszacsatolás
A 8. ábrán látható állapotvisszacsatolásos szabályozás a kaszkád szabályozás kiterjesztésének tekinthető. Az 1. ábrán látható szabályozási körben a kimenő változót csatoljuk vissza. A 4. ábrán látható kaszkád szabályozásban felismertük, hogy a folyamat mérhető belső változóját is célszerű visszacsatolni. A folyamat állapotváltozós modelljének megadásakor n számú belső állapotváltozóval írjuk le a folyamat viselkedését az állapotegyenlettel. Valamennyi állapotváltozó (x vektor) visszacsatolásával kapjuk az állapotvisszacsatolásos szabályozási struktúrát. Ha a kimenőjel is állapotváltozó, akkor a kimenőjelet is visszacsatoljuk. Ha a kimenőjel nem állapotváltozó, akkor annak értéke az állapotváltozókon keresztül alakul ki. Az állapotváltozókat általában konstans erősítésű tagon keresztül csatoljuk vissza.
A beavatkozójel $u=-k^{{\rm T}} x$, ahol $k^{{\rm T}} $ konstans vektor.
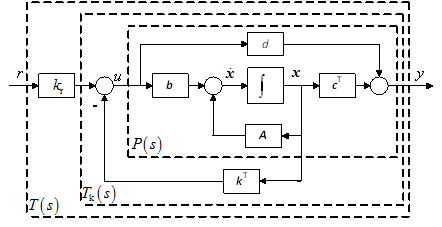
8. ábra Állapotvisszacsatolásos szabályozás
Az így létrehozott szabályozási kör dinamikája eltér a folyamat dinamikájától. A visszacsatolt rendszer pólusai előírhatók oly módon, hogy a szabályozás viselkedése gyorsabb legyen a folyamat dinamikájánál.
Az állapotvisszacsatolás gyorsítja a rendszert, de nem hoz be integráló hatást, így mind az alapjelkövetésnél, mind a zavarelhárításnál statikus hiba lép fel, amit kompenzálni kell.
Egy másik probléma, hogy az állapotváltozók általában nem mérhetők, vagy nem mindegyik állapotváltozó mérhető. Ilyenkor az állapotváltozókat becsülni kell, és az állapotvisszacsatolást a becsült állapotváltozókról kell megvalósítani.
A szabályozás tervezésekor a folyamat modelljéhez először megválasztjuk az adott alkalmazásnak leginkább megfelelő szabályozási struktúrát, majd az adott struktúrában megadjuk a szabályozó algoritmust és meghatározzuk annak paramétereit. Olyan algoritmusokat keresünk, amelyekkel a minőségi előírások teljesíthetők, amelyek lehetőleg kezelni tudják a nagyobb holtidőt is a folyamatban, a meglévő modellezési bizonytalanságok mellett is elfogadható működést biztosítanak.
A különböző szabályozási algoritmusokkal külön foglalkozunk.
References
Åström,K.J., Murray, R.M. Feedback Systems: An Introduction for Scientists and Engineers. Princeton University Press, 2008.
Keviczky, L., Bars, R., Hetthéssy, J., Barta, A., Bányász, Cs. Control Engineering. Széchenyi University Press, 2011.
Garcia, C.E., Morari, M. Internal Model Control 1. A Unifying Review and Some New Results. Industrial & Engineering Chemistry Process Design and Development, 21 (2): 308–323, 1982.
Bars R., Keviczky, L. Control Structures, Control Algorithms, Predictive Control. Int. Symp. on Stability, Vibration and Control of Machines and Structures, SVCS2014, July 3-5, 2014, Belgrade, Serbia.