
Pólusok, zérusok, tervezési megfontolások
Folytonos lineáris rendszereknél a pólusok az átviteli függvény nevezÅjének, a zérusok pedig az átviteli függvény számlálójának zérushelyei.
Mintavételes rendszereknél a pólusok az impulzusátviteli függvény nevezÅjének, a zérusok pedig az impulzusátviteli függvény számlálójának zérushelyei.
A pólusok határozzák meg a rendszer dinamikáját.
Folytonos rendszer
Tekintsük a folytonos rendszer $P(s)$ átviteli függvényét pólus/zérus illetve részlettörtes alakban:
$P\left(s\right)=A\frac{\left(s-z_{1} \right)\left(s-z_{2} \right)\ldots \left(s-z_{m} \right)}{\left(s-p_{1} \right)\left(s-p_{2} \right)...\left(s-p_{n} \right)} =\frac{r_{1} }{s-p_{1} } +\frac{r_{2} }{s-p_{2} } +...+\frac{r_{n} }{s-p_{n} } $
ahol $A$ az erÅsítési tényezÅ, $z_i$ jelöli a zérusokat, $i=1,2,…,m$ és jelöli a pólusokat, $j=1,2,…,n$. $r_j$ a részlettörtes együtthatókat, az ún. reziduálokat adja meg, amelyek értékeit a zérusok értékei befolyásolják.
A rendszer fizikailag realizálható, ha $n\ge m$. Mind a pólusok, mind pedig a zérusok lehetnek valósak, vagy komplex konjugáltak.
A rendszer Dirac impulzusra adott válasza (a rendszer $w(t)$ súlyfüggvénye) a $P(s)$ átviteli függvény inverz Laplace transzformáltja.
$w\left(t\right)=L^{-1} \left\{P\left(s\right)\right\}=\sum _{i=1}^{n}r_{i} {\kern 1pt} {\kern 1pt} e^{p_{i} {\kern 1pt} t}$
A rendszer $v(t)$ egységugrásra adott válasza a súlyfüggvény integrálja.
$v\left(t\right)=L^{-1} \left\{\frac{1}{s} P\left(s\right)\right\}$
A súlyfüggvény akkor lesz lecsengÅ, $\mathop{\lim }\limits_{t\to \infty } w\left(t\right)=0$, ha az átviteli függvény valamennyi pólusának valós része negatív:
$Re\{ p_{i}\} <0$
Ha egy pólus valós, az ahhoz tartozó dinamikus viselkedés aperiodikus. Ha konjugált komplex pólusok vannak, a dinamikában lengések mutatkoznak. Ha a pólus valós része negatív, a lengések szinuszosan csillapodnak, ha a valós rész pozitív, a lengések erÅsödnek.
Két konjugált komplex pólus esetén a reziduálok konjugált imaginárius számok. A hozzájuk tartozó átviteli függvény alábbi alakban adható meg:
$P_{1} \left(s\right)=\frac{j\gamma }{s+\left(\alpha +j\beta \right)} +\frac{-j\gamma }{s+\left(\alpha -j\beta \right)}$
A súlyfüggvény kifejezése:
$w\left(t\right)=j\gamma e^{(-\alpha -j\beta )t} -j\gamma e^{(-\alpha +j\beta )t} =-j\gamma e^{-\alpha t} \left(e^{j\beta t} -e^{-j\beta t} \right)=2\gamma e^{-\alpha t} \sin \beta t$
Ha $\alpha >0$, vagyis a pólusok a komplex számsík negatív térfelén helyezkednek el, a tranziens exponenciálisan lecsengÅ szinuszos függvény.
A két konjugált komplex pólust tartalmazó ún. kéttárolós lengÅ rendszert a legtöbbször $T$ idÅállandójával és $\xi $ csillapítási tényezÅjével adjuk meg:
$P_{1} \left(s\right)=\frac{1}{s^{2} T^{2} +2\xi Ts+1} =\frac{\frac{1}{T^{2} } }{s^{2} +\frac{2\xi }{T} s+1} =\frac{j\gamma }{s+\left(\alpha +j\beta \right)} +\frac{-j\gamma }{s+\left(\alpha -j\beta \right)}$
ahol $\alpha =\frac{\xi }{T} $; $\beta =\frac{1}{T} \sqrt{1-\xi ^{2} } $ és $\gamma =\frac{1}{2T\sqrt{1-\xi ^{2} } } $.
A konjugált komplex pólusokat az 1. ábra mutatja.
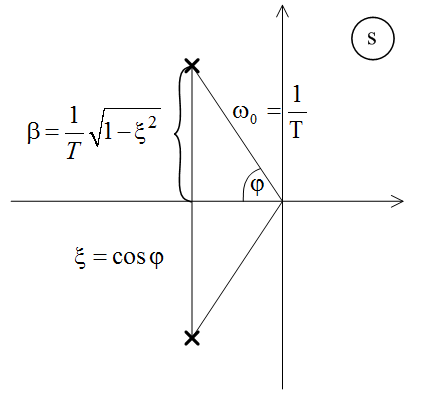
1. ábra Konjugált komplex pólusok
A 2. ábra a kéttárolós lengÅ tag átmeneti függvényeit mutatja különbözÅ csillapítási tényezÅk mellett. Ha $\xi <1$, lengÅ viselkedést kapunk, ha $\xi >1$, a tranziens viselkedés aperiodikus.
Az átviteli függvény pólusai határozzák meg a rendszer dinamikáját. Összefoglalva: valós pólusok aperiodikus, konjugált komplex pólusok lengÅ tranzienseket eredményeznek. Az origóba esÅ pólus integráló hatást jelent. A komplex számsík bal oldalára esÅ pólusok lecsengÅ, a jobb oldalára esÅ pólusok egyre növekvÅ amplitúdójú tranzienseket jelentenek. A 3. ábrán különbözÅ elhelyezkedésÅą pólusokkal rendelkezÅ rendszerek súlyfüggvényeit tüntettük fel.
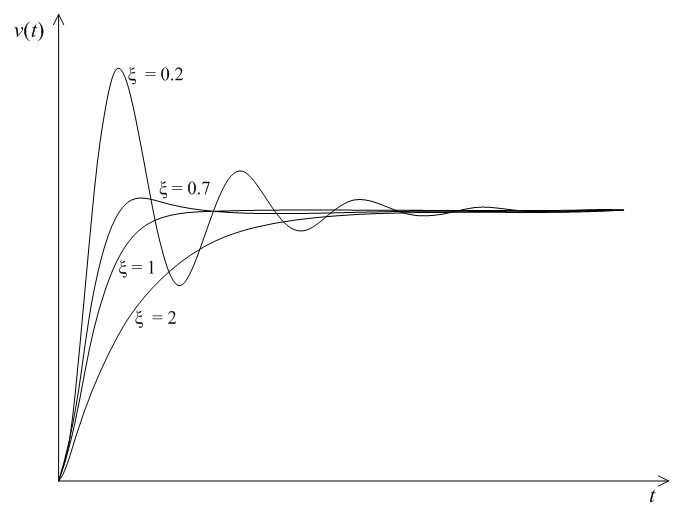
2. ábra Kéttárolós lengÅ tag átmeneti függvényei különbözÅ csillapítási tényezÅk mellett.
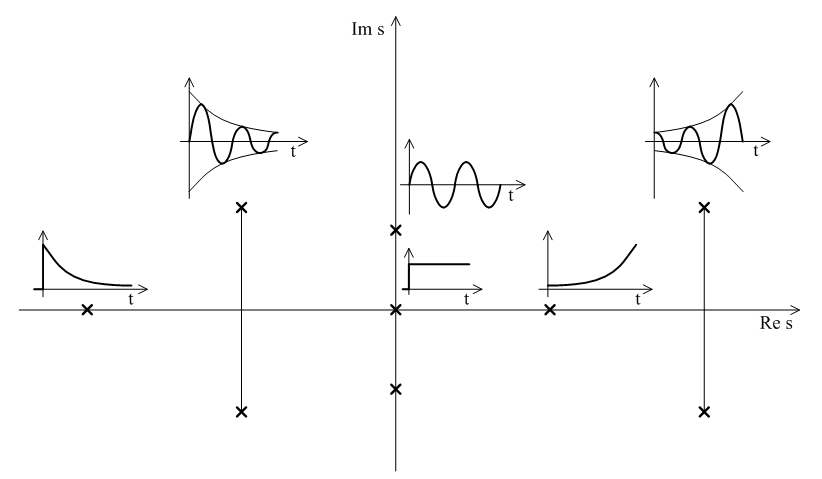
3. ábra Az átviteli függvény pólusi és a súlyfüggvény jellege
Egy rendszer tranziens viselkedése sokkal érzékenyebb a pólusok kis megváltozására, mint a zérusok megváltozására. Ezt egy két pólust és egy zérust tartalmazó rendszer példáján szemléltetjük.
Példa
Legyen a rendszer átviteli függvénye:
$P\left(s\right)=k_{1} \frac{s-z_{1} }{\left(s-p_{1} \right)\left(s-p_{2} \right)} =k_{1} \left(\frac{c_{1} }{s-p_{1} } +\frac{c_{2} }{s-p_{2} } \right)$
$k_1$ normalizáló tényezÅ, amely biztosítja, hogy a rendszer átviteli tényezÅje egységnyi, vagyis egységugrásra adott válasza 1-hez tart.
$k_{1} =-\frac{p_{1} p_{2} }{z_{1} }$
A $c_1$, $c_2$ reziduálok értékei:
$c_{1} =\frac{p_{2} -z_{1} }{p_{2} -p_{1} } $ és $c_{2} =\frac{p_{1} -z_{1} }{p_{1} -p_{2} } $
Az átmeneti függvény kifejezése:
$v\left(t\right)=1-k_{1} c_{1} e^{p_{1} t} -k_{1} c_{2} e^{p_{2} t}$
A pólusok az exponenciális lefutás gyorsaságát határozzák meg. A zérusok az egyes összetevÅk amplitúdóját adják meg.
Legyen $p_{1} =-2$ és $p_{2} =-4$. Vizsgáljuk a zérus hatását az átmeneti függvényre. Legyen a zérus értéke: $z_{1} =-5,-6,-7,-8,-10$ tehát mindkét pólustól balra esik, majd legyen értéke $z_{1} =-2.5,-3,-3.5$, a két pólus közé esik, majd $z_{1} =-1,-1.5$ jobbra esik mindkét pólustól, és végül $z_{1} =1$ és 2, a zérus átkerül a jobb oldali félsíkra. A 4. ábra mutatja az átmeneti függvényeket. Az elsÅ két esetben az átmeneti függvények közötti eltérés kicsi, nagy változás a zérus értékében csak kis mértékben befolyásolja a tranziens viselkedést, a rendszer viselkedése eléggé érzéketlen a zérus értékének megváltozására. A harmadik esetben a zérus lényegesen gyorsítja az átmeneti függvény lefolyását (piros görbe), de ha a zérus túl közel kerül az origóhoz, nagy túllendülést okozhat (zöld görbe). Ha a zérus a jobb oldali félsíkra kerül, az átmeneti függvény elÅször ellenkezÅ irányba indul el, majd visszafordul és eléri a kívánt állandósult értéket (lila és türkiz görbék). Az ilyen rendszert nem-minimumfázisú rendszernek nevezzük, pl. vegyi folyamatok modellezésekor sokszor elÅfordul ilyen viselkedés.
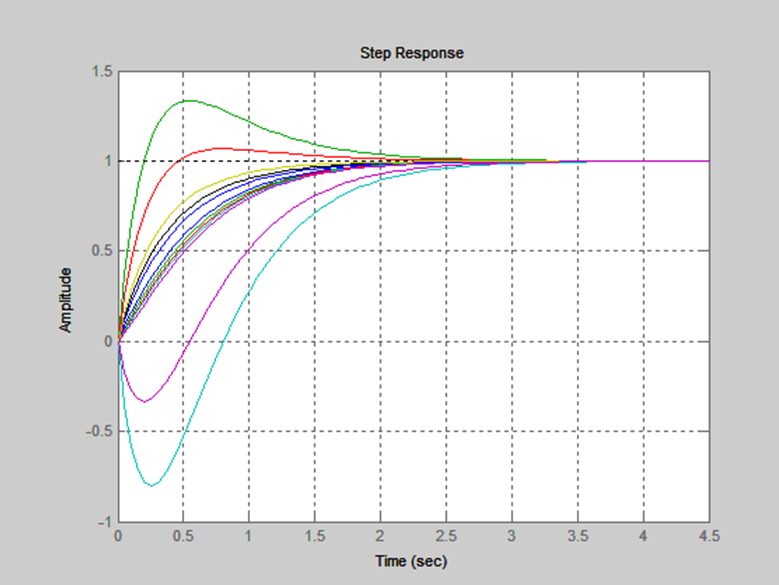
4. ábra A zérus hatása a tranziens viselkedésre
Pólusok és zérusok a folytonos szabályozási körben
A zárt szabályozási kör blokksémáját az 5. ábra mutatja.
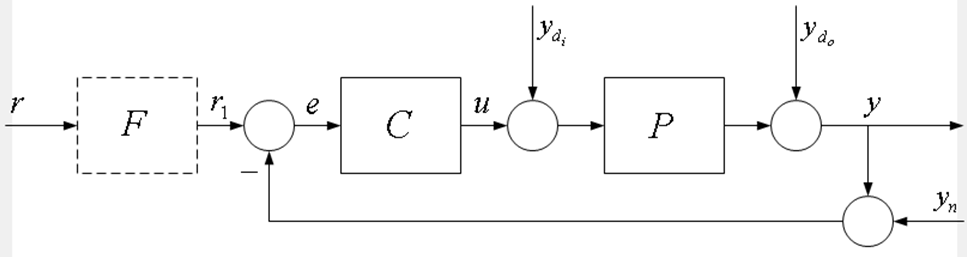
5. ábra Szabályozási kör blokksémája
A szabályozási körben a C szabályozó megfelelÅ megtervezésével biztosítjuk, hogy a negatív visszacsatoláson alapuló szabályozási kör kielégítse a minÅségi elÅírásokat, kövesse az alapjelet és képes legyen a zavarások hatásának kiküszöbölésére. A szabályozási kör dinamikáját a zárt rendszer eredÅ átviteli függvényeinek pólusai határozzák meg. Az eredÅ átviteli függvény az $y$ kimenÅjel és az $r_1$ alapjel között, feltéve, hogy a többi bemenÅjel zérus:
$W\left(s\right)=\frac{Y\left(s\right)}{R_{1} \left(s\right)} =\frac{C\left(s\right)P\left(s\right)}{1+C\left(s\right)P\left(s\right)} =\frac{L\left(s\right)}{1+L\left(s\right)} $
ahol $L\left(s\right)=C\left(s\right)P\left(s\right)$ a felnyitott kör átviteli függvénye.
A zárt rendszer eredÅ átviteli függvényének pólusai határozzák meg a szabályozási kör dinamikáját. A pólusok megegyeznek az
$1+L\left(s\right)=0$
karakterisztikus egyenlet gyökeivel. A gyököknek negatív valós részÅąeknek kell lenniük a stabilis mÅąködés biztosításához.
A $C\left(s\right)$ szabályozót a $P\left(s\right)$ folyamathoz tervezzük úgy, hogy a zárt rendszer megfeleljen a minÅségi elÅírásoknak. Ez azt jelenti, hogy megkívánjuk, hogy a zárt rendszer pólusai biztosítsák a megfelelÅ tranziens viselkedést.
Az egyik megközelítés, hogy elÅírjuk a zárt rendszer kívánt átviteli függvényét, és ebbÅl adódik a szabályozó átviteli függvénye, amelynek realizálhatónak kell lennie (póluselhelyezés). (Póluselhelyezést valósít meg például az állapotvisszacsatoláson alapuló szabályozás.)
A másik megközelítés, hogy a $C\left(s\right)$ szabályozó zérusaival „kiejtjük” a $P(s)$ folyamat kedvezÅtlen, „rossz” pólusait, és ezek helyett a szabályozóval kedvezÅbb pólusokat „hozunk be” a rendszerbe (póluskiejtés). Például a szabályozó zérusával kiejtjük a folyamat nagy idÅállandójához tartozó pólusát, és egy gyorsabb viselkedést jelentÅ pólust hozunk be a szabályozóval, vagy kiejtjük a folyamat nagy idÅállandóját, és helyette behozunk egy integráló hatást, amely biztosítja a pontosabb állandósult állapotbeli viselkedést.
A folyamat labilis pólusát nem szabad a szabályozó zérusával kiejteni, mivel az egészen pontos kiejtés nem lehetséges, és a labilitás benne marad a rendszerben. Nem szabad kiejteni a folyamat nem-minimumfázisú zérusát, mivel ez a szabályozóban egy labilis pólust eredményezne.
A zárt szabályozási kör pólusainak alakulását jól mutatja a gyökhelygörbe, amely a zárt kör pólusait ábrázolja a komplex számsíkon, miközben a rendszer valamelyik paramétere, rendszerint az erÅsítési tényezÅ nulla és végtelen között változik.
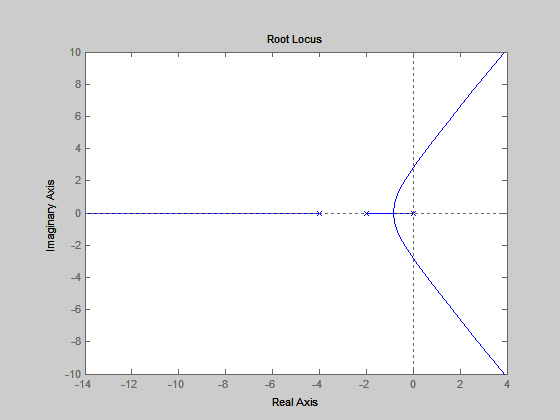
Példaként tekintsük az $L\left(s\right)=\frac{K}{s\left(s+2\right)\left(s+4\right)} $ hurokátviteli függvénnyel adott rendszert. Gyökhelygörbéjét a 6. ábra bal oldala mutatja. Egy adott kritikus erÅsítésig (az a paraméter, ahol a gyökhelygörbe metszi az imaginárius tengelyt) a zárt rendszer pólusai a komplex számsík negatív felén vannak, tehát a szabályozási rendszer stabilis, a kritikus erÅsítésnél nagyobb erÅsítéseknél a pólusok a jobb oldali félsíkra kerülnek, a rendszer labilissá válik. Kis erÅstéseknél a tranziensek aperiodikus lefolyásúak, annál az erÅsítésnél, ahol a gyökhelygörbe kilép a valós tengelybÅl, lengéseket elÅidézÅ pólusok is megjelennek.
 |
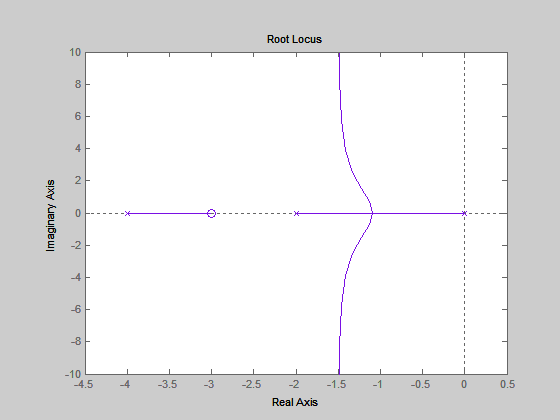 |
6. ábra Integráló kéttárolós rendszer gyökhelygörbéje. A zérus beiktatása strukturálisan stabilissá teszi a rendszert.
Ha a rendszerbe behozunk egy zérust, $L\left(s\right)=\frac{K\left(s+3\right)}{s\left(s+2\right)\left(s+4\right)} $, a gyökhelygörbe a 6. ábra jobb oldala szerint módosul, a zérus „maga felé húzza” az „elszálló” ágat, és így minden erÅsítésnél a pólusok a bal oldali félsíkon maradnak, a rendszer strukturálisan stabilissá válik. Megjegyezzük, hogy analógia adható meg az elektrosztatikus tér és a gyökhelygörbe között. Ha az elektrosztatikus térben a pólusok helyére pozitív töltéseket, a zérusok helyébe pedig negatív töltéseket helyezünk, a kialakuló elektrosztatikus erÅtér erÅvonalainak aszimptotái a gyökhelygörbe alakját mutatják.
Látjuk, hogy a szabályozótervezés a szabályozó struktúrájának és ezen belül pólusainak és zérusainak megfelelÅ megválasztását jelenti. Ugyanakkor a szabályozó megvalósíthatóságát is szem elÅtt kell tartani.
A szabályozótervezéssel a késÅbbiekben részletesebben is foglalkozunk.
Pólusok és zérusok a mintavételes rendszerben
Mintavételes rendszereknél a pólusok az impulzusátviteli függvény nevezÅjének, a zérusok pedig az impulzusátviteli függvény számlálójának zérushelyei.
A folytonos rendszer kimenÅjelét $T_S$ mintavételi idÅvel mintavételezzük. A bemeneten ható mintavételezett jelsorozatot zérusrendÅą tartószerven keresztül adjuk a rendszer bemenetére (7. ábra). Az impulzusátviteli függvény a kimenÅjel és a bemenÅjel $z$-transzformáltjainak hányadosa. A pólusok és a zérusok számértékei nemcsak a folytonos rendszer dinamikájától, hanem a mintavételi idÅtÅl is függnek.
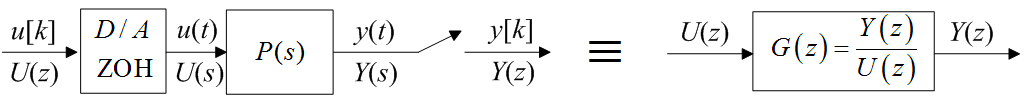
7. ábra Az impulzusátviteli függvény értelmezése
Tekintsünk példaként egy háromtárolós arányos rendszert, amelynek átviteli függvénye:
$P\left(s\right)=\frac{1}{\left(1+sT_{1} \right)\left(1+sT_{2} \right)\left(1+sT_{3} \right)}$
ahol $T_1$, $T_2$, $T_3$ idÅállandók. $T_S$ mintavételi idÅ mellett az impulzusátviteli függvény:
$G\left(z\right)=\frac{Y\left(z\right)}{U\left(z\right)} =\frac{\delta \left(z+\sigma _{1} \right)\left(z+\sigma _{2} \right)}{\left(z-e^{-T_{s} /T_{1} } \right)\left(z-e^{-T_{s} /T_{2} } \right)\left(z-e^{-T_{s} /T_{3} } \right)} $
A folytonos átviteli függvény pólusai ($p_{1} =-1/T_{1} $, $p_{2} =-1/T_{2} $, $p_{3} =-1/T_{3} $) és a mintavételezett rendszer impulzusátviteli függvényeinek pólusai között a megfeleltetés: $p_{d1} =e^{-T_{s} /T_{1} } $, $p_{d2} =e^{-T_{s} /T_{2} } $, $p_{d3} =e^{-T_{s} /T_{3} } $. A folytonos átviteli függvényben nincsenek zérusok. Az impulzusátviteli függvénybe a mintavételezés következtében járulékos zérusok „jöttek be”. A zérusok száma 1-gyel kevesebb a pólusok számánál. A pólus-zérus konfigurációt a 8. ábra szemlélteti. A pólusokat kereszttel, a zérusokat karikával jelöljük. Látható, hogy a pólusok az egységsugarú kör belsejében a jobb oldali félsíkon helyezkednek el. A zérusok a valós tengely bal oldalán helyezkednek el, az egyik zérus az egységsugarú körön kívülre került.
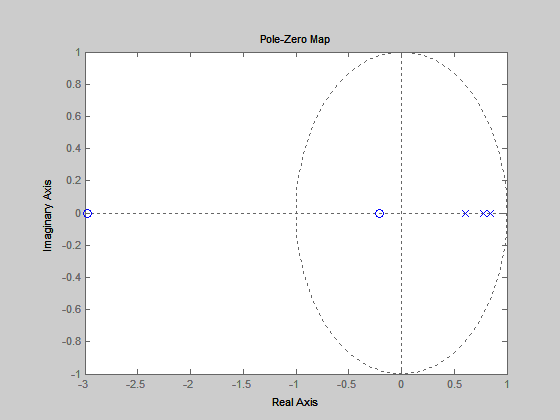
8. ábra Háromtárolós rendszer impulzusátviteli függvényének pólus-zérus konfigurációja
Tekintsük most a kéttárolós lengÅ tag pólusait a folytonos és a diszkrét esetben, miközben a rendszer idÅállandója változik és csillapítási tényezÅje $\xi <1$ állandó.
A lengÅ tag átviteli függvénye:
$P\left(s\right)=\frac{1}{1+2\xi Ts+T^{2} s^{2} }$
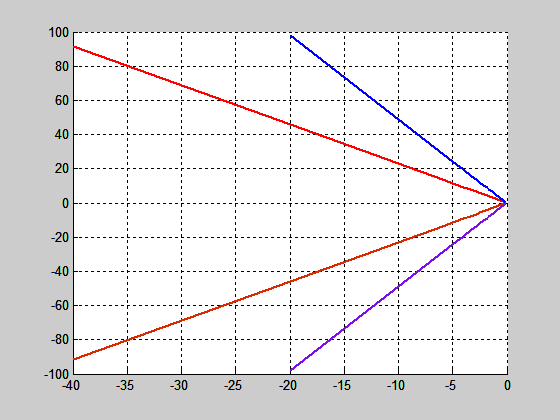
A konjugált komplex pólusok alakulását a folytonos esetre a 9. ábra bal oldala, diszkrét esetre pedig a 9. ábra jobb oldala mutatja. A kék görbék a $\xi =0.2$, a piros görbék a $\xi =0.4$ esetet mutatják. A folytonos rendszer pólusai a diszkrét esetben az ún. „szívgörbébe” képzÅdtek le.
 |
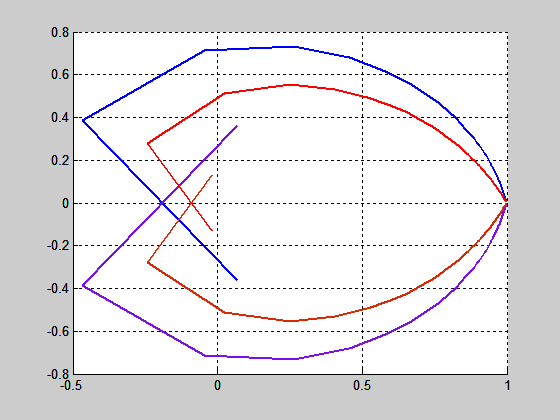 |
9. ábra Kéttárolós lengÅ tag pólusai folytonos és diszkrét esetben
Egy mintavételes zárt szabályozási kör karakterisztikus egyenlete:
$1+L\left(z\right)=0$
A mintavételes rendszer akkor lesz stabilis, ha a karakterisztikus egyenlet valamennyi gyöke (a zárt rendszer impulzusátviteli függvényének pólusai) az egységsugarú kör belsejébe esnek.
A diszkrét szabályozó megfelelÅ tervezésével biztosíthatjuk a szabályozás stabilitását és megfelelÅ statikus és dinamikus tulajdonságait. Most is alkalmazhatjuk a póluselhelyezés illetve a póluskiejtés stratégiáját.
A póluskiejtésnél a szabályozó zérusaival nem szabad kiejteni a folyamat labilis (egységkörön kívülre esÅ) pólusait. A szabályozó pólusaival nem célszerÅą kiejteni a folyamat „rossz” zérusait, amelyek az egységkörön kívülre, illetve lengÅ tagok esetén a „szívgörbén” kívülre esnek. Ezeknek a zérusoknak a kiejtése labilis, illetve gyengén csillapított pólusokat hoznának be a szabályozóba, és ezáltal labilis mÅąködés jönne létre a szabályozási körben, illetve a mintavételi pontok között csillapított lengések jönnének létre.
A mintavételes rendszer szabályozó tervezésének néhány kérdésével a késÅbbiekben kissé részletesebben foglalkozunk.