

A szabályozás fĹkérdése: stabilitás
A szabályozás negatív visszacsatoláson alapul. A folyamat kimenĹjelét érzékeljük, majd összehasonlítjuk a kívánt alapjellel. A különbségi jel a szabályozó bemenĹjele, amely a folyamat beavatkozójelét képezi.
Fontos tehát az információáramlás iránya, és a kör zárása.
A negatív visszacsatolásnak számos elĹnyös tulajdonsága van. Azonban a folyamat tehetetlensége (idĹállandói, holtideje) miatt csak késleltetve válaszol a bemenĹjel változásaira. Ahhoz, hogy a zárt kör mĹąködni kezdjen, eltérésnek, hibának kell fellépnie, amire a visszacsatolt kör csak késleltetve válaszol. Ez a késleltetés labilis viselkedést eredményezhet, a kimenĹjel „megszaladhat”, amit a szabályozó megfelelĹ megtervezésével mindenképpen el kell kerülni.
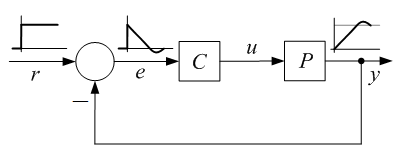
1. ábra Szabályozási kör
Nagy átviteli tényezĹk mellett a késleltetés idĹtartama alatt a kimenĹjel értéke annyira „megszaladhat”, hogy a szabályozás már nem képes visszaszabályozni azt a kívánt értékre. A szabályozó struktúráját és paramétereit úgy kell megválasztani, hogy a szabályozás stabilis legyen.
A labilis viselkedés kialakulásának érzékeltetésére tekintsük az 1. ábrán látható szabályozási kört. Az alapjel egységugrásszerĹą változásakor a kimenĹjel nulláról indulva növekedni kezd. A hibajel értéke egyrĹl kiindulva csökken. Ha a szabályozó erĹsítése nagy, a folyamat (szakasz) bemenetén kezdetben nagy bemenĹjel jelenik meg, amely a szakasz kimenĹjelének gyors felfutását eredményezi. A változás dinamikáját a P folyamat és a C szabályozó dinamikája, átviteli tényezĹi és idĹállandói határozzák meg. Mikor a kimenĹjel eléri az alapjel által meghatározott értéket, a hibajel nulla értéket vesz fel. A jelek azonban a rendszer tehetetlensége miatt nem állnak be azonnal a kívánt értékükre, hanem az addigi meredekséggel tovább változnak. Ha a kimenĹjel túllendül elĹírt értékén, a hibajel negatívvá válik, ami egy idĹ után csökkenteni fogja a kimenĹjel értékét. A szakasz és a szabályozó nagy idĹállandói és nagy átviteli tényezĹi mellett a túllendülés jelentĹs lehet. A rendszerben állandósult vagy egyre növekvĹ lengések jelenhetnek meg. A stabilitás problémáját az okozza, hogy a rendszer a rendelkezĹjel (hibajel) által szolgáltatott információt késleltetve használja fel, és nagy átviteli tényezĹk mellett a késleltetés idĹtartama alatt a kimenĹjel értéke annyira "megszalad", hogy a szabályozás már nem képes visszaszabályozni azt a kívánt értékre. A szabályozó struktúráját és paramétereit úgy kell megválasztani, hogy a szabályozás stabilis legyen. Ezt a jelenséget tapasztaljuk például zuhanyozáskor, ha nem várjuk meg, míg a beavatkozás, a hideg vagy meleg vízcsap állításának hatása a zuhanycsövön keresztül eléri testünket, és türelmetlenül újból és újból állítgatjuk a csapokat (2. ábra).
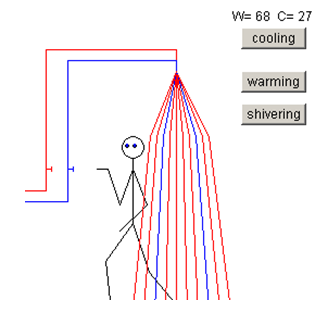
2. ábra A zuhanyozáskor labilis szabályozást érhetünk el, ha a beavatkozásnál nem várjuk meg a holtidĹ hatását
Néha elĹfordul, hogy maga a folyamat labilis, és a szabályozással kívánjuk stabilizálni. A 3. ábrán látható zsonglĹr az eldĹlni kívánó rudat (inverz ingát) stabilizálja a mozgásával, érzékeli a rúd helyzetét és sebességét és ennek megfelelĹen mozogva egyensúlyoz.
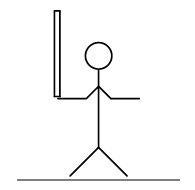
3. ábra A zsonglĹr mozgásával stabilizálja a rúd mozgását
A 4. ábra a feladat automatikus szabályozással való megoldását szemlélteti.
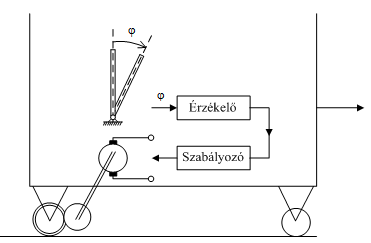
4. ábra Inverz inga mozgásának stabilizálása automatikus szabályozással
A stabilitás fogalma, megfogalmazása
A stabilitás a rendszernek az a tulajdonsága, hogy egyensúlyi állapotából kimozdítva újra egyensúlyba képes kerülni.
Ha a rendszer nemlineáris, a stabilitás a bemenĹjeltĹl és a munkaponttól is függ. Ebben az esetben a stabilitás nem a rendszernek, hanem a rendszer egy állapotának a jellemzĹje. Lineáris rendszer esetén a stabilitás a rendszer jellemzĹje, a rendszer struktúrájától és paramétereitĹl függ, de független a bemenĹjeltĹl.
A stabilitásnak több meghatározása is létezik.
A magára hagyott rendszer stabilitása. A rendszer stabilis, ha nyugalmi állapotából kimozdítva majd magára hagyva visszatér eredeti állapotába. Ha eredeti állapotától eltávolodik, mĹąködése labilis. Határesetben nem tér ugyan vissza a nyugalmi állapotba, de nem is távolodik el attól, hanem annak a kitérítés mértékétĹl függĹ környezetében marad (például a kiindulási állapot körül korlátos amplitúdójú csillapítatlan lengéseket végez). Nemlineáris rendszereknél stabilisnak tekintjük a rendszert akkor is, ha a határesetben a kimozdítás után a nyugalmi állapot tetszĹlegesen elĹírható kis környezetébe tér vissza. A rendszer aszimptotikusan stabilis, ha egyensúlyi állapotából való kimozdítása után visszatér kiindulási helyzetébe. Egy stabilis lineáris rendszer aszimptotikusan stabilis. Egy lineáris rendszer $w\left(t\right)$ súlyfüggvénye aszimptotikus stabilitás esetén lecsengĹ,
$\lim \limits_{t\to \infty } w\left(t\right)=0 $
illetve abszolút integrálható:
$\int _{0}^{\infty }\left|w\left(t\right)\right| {\rm d}t<\infty $
A gerjesztett rendszer stabilitása. Stabilis a rendszer, ha korlátos bemenĹjelre korlátos kimenĹjellel válaszol bármilyen kezdeti feltétel mellett. A gerjesztett rendszer stabilitását BIBO (Bounded-Input – Bounded Output) stabilitásnak is nevezik.
Lineáris rendszerben a stabilitás a rendszer tulajdonsága. A stabilitás nem függ a gerjesztés nagyságától. Ha egy lineáris rendszerben a magára hagyott rendszer stabilis, a gerjesztett rendszer is stabilis lesz. A stabilitás egyértelmĹąen megítélhetĹ valamilyen egyszerĹą bemenĹjelre adott válaszból.
BelsĹ stabilitás. Vizsgáljuk a szabályozási rendszerben valamennyi kimenĹjel (kimenĹjel, beavatkozójel, hibajel) alakulását valamennyi bemenĹjel (alapjel, kimeneti és bemeneti zavarás) hatására. A rendszer stabilis, ha a vizsgált valamennyi korlátos bemenĹjelre valamennyi kimenĹjel is korlátos.
Ljapunov stabilitás. Lagrange energiaelmélete szerint egy rendszer akkor van egyensúlyban, ha potenciális energiája minimális. Ljapunov a rendszert leíró differenciálegyenlethez vagy állapotegyenlethez egy energia tulajdonságú ún. Ljapunov skalár függvény meghatározását írja elĹ. Ha ez a függvény az állapotváltozók vizsgált tartományában pozitív, és deriváltja negatív, a rendszer aszimptotikusan stabilis. Ljapunov vizsgálati módszerei elégséges feltételeket adnak nemlineáris rendszerek stabilitási viszonyainak meghatározására.
A folytonos idejĹą lineáris szabályozási rendszer stabilitásának matematikai megfogalmazása
A magára hagyott zárt szabályozási rendszer akkor aszimptotikusan stabilis, ha a tranziens mozgását leíró idĹfüggvény csillapodó összetevĹkbĹl áll. A tranziens idĹfüggvény olyan exponenciális összetevĹk kombinációja, amelyek kitevĹi a rendszer karakterisztikus egyenletének a gyökei.
Irányítható és megfigyelhetĹ rendszerben (amikoris a szabályozó zérusai nem ejtik ki a szakasz pólusait) a karakterisztikus egyenlet gyökei megegyeznek a zárt rendszer eredĹ átviteli függvényének pólusaival. A rendszert leíró differenciálegyenlet karakterisztikus egyenlete formailag megegyezik a zárt rendszer eredĹ átviteli függvényének nevezĹjével.
Ugyanis a zárt rendszer eredĹ átviteli függvénye az $y$ kimenĹjel és az $r$ alapjel között:
$T\left(s\right)=\frac{y\left(s\right)}{r\left(s\right)} =\frac{C\left(s\right)P\left(s\right)}{1+C\left(s\right)P\left(s\right)} =\frac{C\left(s\right)P\left(s\right)}{1+L\left(s\right)} $
A karakterisztikus egyenlet pedig formailag megegyezik az
$1+L\left(s\right)=0 $
egyenlettel. A karakterisztikus egyenlet gyökei tehát megegyeznek a zárt rendszer eredĹ átviteli függvényének pólusaival.
Ha a felnyitott kör átviteli függvénye racionális törtfüggvény, $L(s)=\frac{N(s)}{D(s)} $, ahol $N(s)$ és $D(s)$ polinomok, a karakterisztikus egyenlet a következĹ alakban is megadható:
$D(s)+N(s)=0 $
illetve
$a_{n} s^{n} +a_{n-1} s^{n-1} +...+a_{1} s+a_{0} =a_{n} (s-p_{1} )(s-p_{2} )...(s-p_{n} )=0 $
Ha a rendszert állapotegyenletével írjuk le, amelynek állapotmátrixa A, a karakterisztikus egyenlet a
$\det (sI-A)=0 $
összefüggéssel adható meg.
Az aszimptotikus stabilitásnak az a feltétele, hogy a zárt rendszer $p_{i} $ pólusai negatív valós részĹąek legyenek, mivel ezek eredményeznek idĹben lecsengĹ tranzienseket. A feltétel úgy is megfogalmazható, hogy a zárt szabályozási kör akkor aszimptotikusan stabilis, ha valamennyi pólusa a komplex számsík bal oldalára esik.
Ha bármelyik pólus a jobb oldali félsíkra esik, a rendszer labilis. Ha a bal oldali félsíkra esĹ pólusokon kívül a képzetes tengelyen az origóban is van pólus, a rendszerben integráló hatás van, és tranziense ugyancsak a végtelenbe tart. Ha a képzetes tengelyen egyszeres konjugált komplex pólusok vannak, a tranziensekben csillapítatlan lengések lépnek fel. Többszörös pólusok esetén a lengések növekvĹ amplitúdójúak. A gyakorlatban a zárt rendszernek csak az aszimptotikus stabilitása elfogadható.
A stabilitás vizsgálatához tehát a karakterisztikus egyenlet gyökeit kell meghatározni. A gyökök meghatározására zárt képlet csak a negyedfokú esetig létezik. Magasabbfokú egyenlet gyökeinek meghatározására numerikus eljárások alkalmazhatók. A gyökök és az algebrai egyenlet együtthatói között fennálló összefüggéseket felhasználó analitikus módszerek vannak annak eldöntésére, hogy a karakterisztikus egyenlet valamennyi gyöke bal oldali-e.
Stabilitásvizsgálat a gyökhelygörbe alapján
A gyökhelygörbe a karakterisztikus egyenlet gyökeit adja meg a komplex számsíkon, miközben a rendszer valamelyik paramétere (a leggyakrabban a körerĹsítés) nulla és végtelen között változik.
Ha a gyökök a bal oldali félsíkra esnek, a rendszer stabilis. A kritikus körerĹsítésnél a gyökhelygörbe metszi az imaginárius tengelyt. Azon körerĹsítéseknél, ahol a gyökhelygörbe átkerül a jobb oldali félsíkra, a rendszer labilissá válik.
A gyökhelygörbe alapján nemcsak a rendszer stabilitása dönthetĹ el, hanem a gyökök elhelyezkedésébĹl a rendszer dinamikus tulajdonságai is hozzávetĹlegesen meghatározhatók.
A gyökhelygörbe megrajzolásához elvileg a karakterisztikus egyenletet kell megoldani különbözĹ paraméterértékek mellett. Megjegyezzük, hogy számos szabály könnyíti meg a gyökhelygörbe felrajzolását.
Az 5. ábra egy 3 pólust tartalmazó rendszer gyökhelygörbéjét mutatja. (A pólusokat az ábrán kereszttel jelöljük.) A zárt rendszernek is 3 pólusa van, amelyek közül 2 az erĹsítés növelésével konjugált komplex-szé válik, majd egy kritikus erĹsítés elérésekor 2 gyök az imaginárius tengelyre esik, és a zárt rendszer a stabilitás határára kerül, a rendszerben állandósult lengések jönnek létre. Ha az erĹsítést tovább növeljük, két gyök a jobb oldali félsíkra kerül és a zárt rendszer labilissá válik. Iktassunk a rendszerbe egy zérust. A gyökhelygörbét erre az esetre a 6. ábra mutatja. (A zérust körrel jelöljük.) A zérus maga felé „húzza” a gyökhelygörbe ágakat, amelyek most a bal oldali félsíkon maradnak. A zérus beiktatása stabilizálta a rendszert. Nagy erĹsítéseknél most is fellépnek a zárt rendszerben csillapodó lengések a konjugált komplex pólusok miatt.
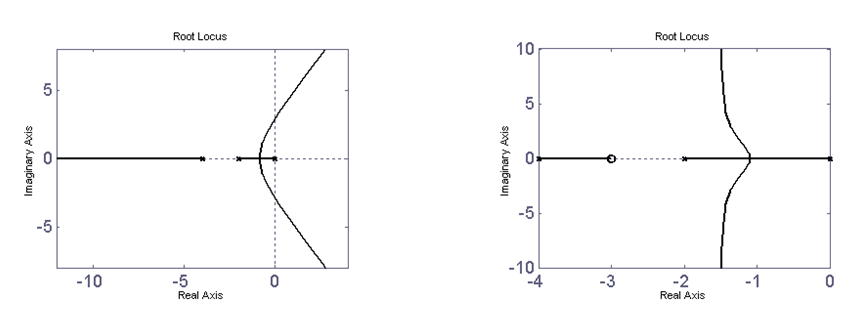
5-6. ábra A zérus maga felé „húzza” a gyökhelygörbe ágakat
A Nyquist stabilitási kritérium
A gyökhelygörbe szemléletes képet ad a szabályozási kör karakterisztikus egyenlete gyökeinek alakulásáról egy változó paraméter függvényében, így átfogó képet kaphatunk a rendszer stabilitási és dinamikus viszonyairól.
HoltidĹs rendszerek esetén azonban a karakterisztikus egyenlet nem polinomiális egyenlet, így a gyökök csak közelítĹ eljárással határozhatók meg közelítĹen.
Ilyen esetben is alkalmazható azonban a Nyquist stabilitási kritérium. Itt ennek csak egyszerĹąsített esetével foglalkozunk, mikor maga a folyamat stabilis, és a visszacsatolás által válhat labilissá. A kritérium általános esetét a hivatkozott irodalmak tárgyalják.
A Nyquist kritérium alapján a felnyitott kör frekvenciadiagramjából következtethetünk a zárt rendszer stabilitására. A módszer szemléletes, és labilitás esetén könnyen megadható, hogyan célszerĹą a szabályozási kör struktúráját és paramétereit módosítani. A frekvenciafüggvény megfelelĹ alakításával – járulékos zérusok és pólusok beiktatásával – formálhatjuk a frekvenciafüggvényt a zárt kör elĹírt tulajdonságainak, stabilitásának, statikus és dinamikus tulajdonságainak biztosítására.
A csillapítatlan lengés kialakulásának szemléltetése a frekvenciatartományban
A zárt szabályozási rendszer karakterisztikus egyenlete $1+L\left(s\right)=0$, ahol $L(s)$ a felnyitott kör átviteli függvénye. $s=j\omega $ helyettesítéssel vizsgálhatjuk, hogy az egyenletnek van-e megoldása az imaginárius tengelyen. Ha van olyan $\omega _{0} $ frekvencia, amelyre teljesül az $1+L(j\omega _{0} )=0$, illetve az $L(j\omega _{0} )=-1$ feltétel, a zárt rendszerben ezen a körfrekvencián csillapítatlan lengések keletkeznek, a rendszer a stabilitás határára kerül. Ekkor a felnyitott kör Nyquist diagramja áthalad a komplex számsík $-1+j0$ pontján.
A csillapítatlan lengés kialakulását a következĹképpen szemléltethetjük. Tekintsük a 7. ábrán látható szabályozási kört. A felnyitott kör Nyquist diagramja az $\omega _{0} $ körfrekvencián áthalad a -1 ponton. Képzeletben nyissuk fel a rendszert a B-K pontnál. Legyen a rendszer $r$ alapjele $\omega _{0} $ körfrekvenciájú szinuszos jel. Ezt a jelet a rendszer azonos amplitudóval, de ellenkezĹ elĹjellel viszi át. Ha most a B-K pontokat összekötjük, a negatív visszacsatolás miatt az e hibajel megegyezik a bemeneti szinuszos jellel. Ez a csillapítatlan szinuszos jel akkor is fennmarad a rendszerben, ha az alapjelet megszüntetjük. Ilyen frekvenciájú lengések jönnek létre a rendszerben akkor is, ha az alapjel az adott szinuszos jeltĹl eltérĹ, más determinisztikus jel, például egységugrás. Ugyanis az alapjel frekvenciaspektrumában valamennyi frekvencia elĹfordul, ezekbĹl a szinuszos összetevĹkbĹl az alapjel felépíthetĹ. Az $\omega _{0} $ körfrekvenciájú összetevĹ a rendszerben fennmarad.
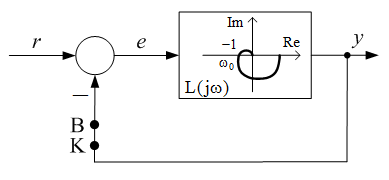
7. ábra A Nyquist diagram a stabilitás határhelyzetében áthalad a -1 ponton
Az egyszerĹąsített Nyquist stabilitási kritérium
Tételezzük fel, hogy a felnyitott kör átviteli függvényének nincsenek jobb oldali pólusai, tehát a felnyitott rendszer stabilis.
Rajzoljuk fel a frekvenciafüggvényt a komplex számsíkon az $-\infty <\omega <\infty $ tartományra (teljes Nyquist diagram). Járjuk körül a Nyquist diagramot a növekvĹ frekvenciák irányában.
Ha a Nyquist diagram nem veszi körül a $-1+j0$ pontot, a zárt szabályozási kör stabilis.
Ha a Nyquist diagram áthalad a $-1+j0$ ponton, a rendszer a stabilitás határán van.
Ha a Nyquist diagram körülveszi a $-1+j0$ pontot, a rendszer labilis.
EgyszerĹąbb megfogalmazásban: ElegendĹ a Nyquist diagramot a pozitív $\omega $ értékekre felrajzolni. Ha a diagramot $\omega =0$-tól $\infty $-ig végigjárjuk, és a $-1+j0$ pont a görbétĹl bal kéz felé esik, a zárt szabályozási rendszer stabilis. Ha a görbe áthalad a $-1+j0$ ponton, a rendszer a stabilitás határán van. Ha a $-1+j0$ pont a görbétĹl jobb kéz felé esik, a rendszer labilis. (A bizonyítás a hivatkozott irodalomban megtalálható.)
Ezek szerint a 8. ábrán a $K_{1} $ erĹsítéssel a rendszer stabilis, míg a $K_{2} $ erĹsítéssel labilis.
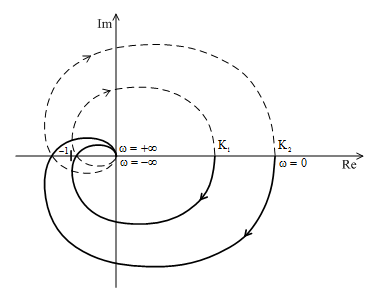
8. ábra Háromtárolós rendszer stabilitása
Példa
A felnyitott kör átviteli függvénye: $L\left(s\right)=\frac{K}{\left(1+sT\right)^{3} } $. Merev (egységnyi) negatív visszacsatolást alkalmazunk. Határozzuk meg a $K_{krit} $ kritikus erĹsítést, amelynél a zárt szabályozási kör a stabilitás határára kerül.
A felnyitott kör Nyquist diagramját a stabilitás határhelyzetében a 9. ábra mutatja.

9. ábra A felnyitott kör Nyquist diagramja
A Nyquist diagram az $\omega _{0} $ körfrekvencián áthalad a komplex számsík -1 pontján. Ezen a körfrekvencián a frekvenciafüggvény fázisszöge -180Ë, abszolút értéke pedig 1.
$\varphi \left(\omega _{0} \right)=-3arctg\omega _{0} T=-180^{\circ } $, ahonnan $\omega _{0} T=\sqrt{3} $,
$\frac{K_{krit} }{\left(\sqrt{1+\omega _{0}^{2} T^{2} } \right)^{3} } =1$ tehát $K_{krit} =8$ függetlenül a $T$ idĹállandó értékétĹl.
A stabilitás mutatószámai
Stabilis felnyitott kör esetén tehát a zárt szabályozási kör akkor stabilis, ha a Nyquist diagram nem veszi körül a $-1+j0$ pontot. Mondhatjuk, hogy a rendszernek stabilitási tartaléka van, ha a Nyquist diagramot „kellĹen távol tartjuk” a $-1+j0$ ponttól.
Definiálhatunk mérĹszámokat, amelyek jelzik, milyen messze van a felnyitott rendszer Nyquist diagramja a $-1+j0$ ponttól. Ilyen mérĹszámok a fázistartalék vagy fázistöbblet (phase margin), az erĹsítési tartalék (gain margin), a modulus tartalék (modulus margin) és a késleltetési tartalék (delay margin).
Fázistartalék vagy fázistöbblet
Rajzoljuk fel a felnyitott rendszernek a pozitív frekvencia értékekhez tartozó Nyquist diagramját. Határozzuk meg a Nyquist diagramnak az egységsugarú körrel való metszéspontját. A metszésponthoz tartozó körfrekvenciát vágási körfrekvenciának nevezzük és $\omega _{c} $-vel (cut-off frequency) jelöljük. Kössük össze egy egyenessel az origót és metszéspontot. Ennek az egyenesnek a negatív valós tengellyel bezárt szögét fázistartaléknak vagy fázistöbbletnek nevezzük (10. ábra).
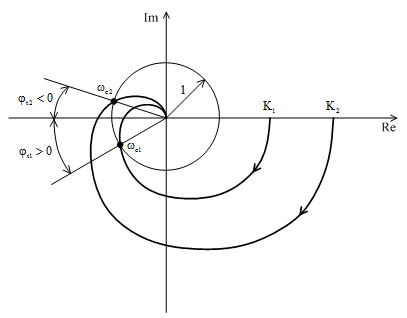
10. ábra A fázistöbblet értelmezése
A fázistöbblet kifejezése:
$\varphi _{t} =\varphi \left(\omega _{c} \right)+180^{\circ } $
Ha a fázistöbblet pozitív, a rendszer stabilis. Ha fázistöbblet zérus, a rendszer a stabilitás határán van. Ha a fázistöbblet negatív, a rendszer labilis.
Tehát
$\varphi _{t} >0$ Stabilis rendszer
$\varphi _{t} =0$ Határhelyzet
$\varphi _{t} <0$ Labilis rendszer
A fázistöbblet, mint egyetlen mérĹszám alapján akkor ítélhetjük meg a rendszer stabilitását, ha a Nyquist diagram csak egyszer metszi az egységsugarú kört.
ErĹsítési tartalék
Határozzuk meg a Nyquist diagramnak a negatív valós tengellyel való metszékét. Ha ez az érték $\kappa <1$, a rendszer stabilis. Ha $\kappa =1$, a rendszer a stabilitás határán van. Ha $\kappa >1$, a rendszer labilis. A $\kappa $ metszék reciprokát erĹsítési tartaléknak nevezzük. Az erĹsítési tartalék értékével megszorozva a körerĹsítést, a kritikus körerĹsítés értékét kapjuk meg.
Tehát
$\kappa <1$ Stabilis rendszer
$\kappa =1$ Határhelyzet
$\kappa >1$ Labilis rendszer
Az erĹsítési tartalék, mint egyetlen mérĹszám alapján akkor ítélhetjük meg a rendszer stabilitását, ha a Nyquist diagram csak egyszer metszi negatív valós tengelyt.
A stabilitás mellett a megfelelĹ tranziens viselkedéshez, a zárt rendszer átmeneti függvényében a kb. 10% alatti túllendülés biztosításához a megkívánt fázistöbblet 60Ë körüli, az erĹsítési tartalék megkívánt értéke pedig kb. 2. Ezek az értékek akkor mérvadók, ha a felnyitott körben nincsenek kis csillapítási tényezĹjĹą lengĹ tagok.
Késleltetési tartalék
A késleltetési tartalék megadja a holtidĹnek azt a $\tau _{m} $ legkisebb értékét, amelyet a felnyitott körbe sorosan beiktatva a zárt rendszer a stabilitás határára kerül. A késleltetési tartalék a radiánban mért fázistöbbletbĹl az alábbi összefüggéssel számítható ki:
$\tau _{m} =\frac{\varphi _{t} }{\omega _{c} } $, ahol $\omega _{c} $ a vágási körfrekvenciát jelöli.
A stabilitási tartalékok alapján nemcsak a stabilitást dönthetjük el, hanem azt is megállapíthatjuk, „milyen messze van” a rendszer a stabilitás határától.
A stabilitás megítélése a Bode diagramból
A fázistöbblet és az erĹsítési tartalék a felnyitott rendszer Bode diagramjából is leolvasható. Az $\omega _{c} $ vágási körfrekvenciánál a frekvenciafüggvény abszolút értéke egységnyi. A Bode amplitúdó-körfrekvencia jelleggörbe ennél a frekvenciánál metszi a vízszintes nulla dB tengelyt. Az ehhez a körfrekvenciához tartozó fázisszögnek a -180Ë-tól való eltérése adja a fázistöbbletet. A $\varphi =-180^{\circ } $-hoz tartozó frekvenciánál leolvasott abszolút érték meadja a $\kappa $ paraméter értékét dB-ben, amibĹl meghatározható az erĹsítési tartalék (11. ábra).
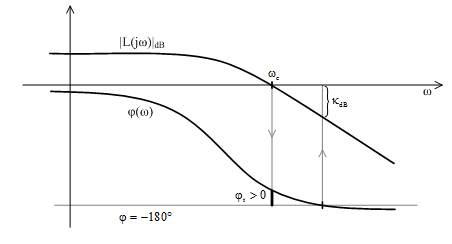
11. ábra A stabilitás megítélése a Bode diagramból
Ha a felnyitott kör minimumfázisú (átviteli függvénye nem tartalmaz jobb oldali zérusokat és pólusokat), továbbá a szabályozási kör nem tartalmaz holtidĹs tagot, a stabilitás igen egyszerĹąen megállapítható a felnyitott kör közelítĹ amplitúdó-körfrekvencia görbéje alapján.
Egy minimumfázisú holtidĹmentes szabályozási rendszer stabilis, ha a felnyitott kör aszimptotikus Bode diagramja a -20dB/dekád meredekségĹą szakaszon metszi a frekvenciatengelyt. A rendszer biztosan labilis, ha a metszés meredeksége -60dB/dekád vagy ennél nagyobb. Ha a metszési szakasz meredeksége -40dB/dekád, a rendszer lehet stabilis vagy labilis is, de fázistartaléka biztosan megengedhetetlenül kicsi. (Az állítások igazolása megtalálható a hivatkozott irodalomban.) A stabilitás biztosításához tehát a vágási körfrekvenciának -20dB/dekád meredekségĹą szakaszra kell esnie. (Ez a szakasz legyen elegendĹen hosszú, hogy a fázistöbblet is megfelelĹ, 60°körüli legyen.)
Hivatkozások:
Keviczky, Bars, Hetthéssy, Barta, Bányász. Szabályozástechnika, 2009, MĹąegyetemi Kiadó, 55079 with the agreement of the authors.
Åström, K.J., Murray, R.M. Feedback Systems: An Introduction for Scientists and Engineers. Princeton University Press, 2008.
Szilágyi, B. Szabályozástechnika. Számítógépes gyakorlatok. Irányítástechnika és Informatika Tanszék, 1998.
