
A negatív visszacsatolás
A rendszerek változóit, kimeneteit valamint belső változóit irányítani kell.
Az irányítás célja annak biztosítása, hogy a rendszer kimenőjele minél jobban kövesse kívánt, előírt értékét, az alapjelet, minél jobban kiküszöbölje a zavarások hatását, kevéssé legyen érzékeny a mérési zajokra és a rendszer paramétereinek pontatlanságaira.
Az irányítás tervezése során olyan rendszert kívánunk létrehozni, amellyel az előírt minőségi követelmények biztosíthatók, a rendszer korlátait figyelembe vesszük, továbbá a szabályozó műszakilag reálisan megvalósítható, és gazdasági és esetleges egyéb szempontoknak (pl. környezetvédelem) is megfelel.
Az irányítás során érzékeljük, mérjük a rendszer irányítandó jeleit, és amennyiben ezek eltérnek kívánt értékeiktől, döntést hozunk a beavatkozásra, a beavatkozó bemenőjel módosítására.
Az irányítás történhet nyitott és zárt körben.
Ha az ítéletalkotáshoz az információt nem a folyamat kimenőjeléről, hanem más forrásból vesszük, vagy előzetes ismereteket használunk fel, vezérlésről beszélünk. Ilyenkor az irányítás nyitott körben valósul meg (1. ábra). Az ábrán P a folyamat, C az irányító berendezés átviteli függvényét jelöli, r az alapjel, y a folyamat kimenőjele, $y_{{\rm di}} $ a bemeneti, $y_{{\rm do}} $ a kimeneti zavarás.
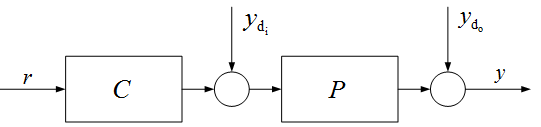
1. ábra Vezérlés
Az alapjelkövetés ideális lenne, ha az irányító berendezés a folyamat átviteli függvényének inverzét valósítaná meg. Vezérléssel megvalósítható az alapjelkövetés, azonban a vezérlés nem képes a zavarások hatásának kiküszöbölésére.
A folyamat tökéletes inverze többnyire nem realizálható. (Ha például a folyamat holtidős késleltetést tartalmaz (a kimenőjel a bemenőjel változását követően csak késleltetve jelenik meg), annak inverze a folyamat jövőbeni értékeinek megadását jelentené.)
Az irányítás negatív visszacsatolás útján valósul meg, ha a folyamat beavatkozó jelét a mért jellemző és annak kívánt, előírt értéke közötti különbség befolyásolja. A mért érték rendszerint az $y_{{\rm n}} $ mérési zajjal terhelt. Az e rendelkezőjel alapján a C szabályozó létrehozza az u beavatkozójelet, amely módosítja a P szakasz kimenőjelét. A folyamat kimenőjele a folyamat dinamikájától függő módon addig változik, amíg a kimenőjel el nem éri kívánt értékét. A negatív visszacsatolással létrejövő irányítást szabályozásnak nevezzük. A szabályozást speciális feladatokat megvalósító elemek, ún. szervek (érzékelő, alapjelképző, különbségképző, szabályozó, beavatkozó szervek) összekapcsolásával valósítjuk meg. A szerveket az adott folyamathoz választjuk meg. Különböző fizikai mennyiségek érzékelésére különböző érzékelő szervek választhatók. Lényeges ezek mérési tartománya, pontossága, zajérzékenysége, stb. A beavatkozószervek a folyamat beavatkozó mennyiségét befolyásolják, lehetnek pl. szelep helyzetét beállító motorok.
A szabályozás szerkezeti vázlata az egyes berendezések, szervek megvalósítását és egymáshoz kapcsolódását mutatja. A működési vázlat (2. ábra) a berendezéseket dobozokkal ábrázolja, feltüntetve bemenő- és kimenőjeleiket és megadja egymáshoz kapcsolódásukat.
2. ábra Szabályozás működési vázlata
A szabályozás vázlatát, a különböző funkciójú elemek egymáshoz kapcsolódását, az ún. hatásvázlatot a 3. ábra adja meg. A hatásvázlatban a dobozokba a tagok jelátvitelét jellemző jelleggörbéket illetve matematikai összefüggéseket (pl. átviteli függvényeket) írjuk be. A hatásvázlat alapján a szabályozási rendszer viselkedése vizsgálható, a minőségi előírások teljesítésére a szabályozó megtervezhető. Sokszor az alapjelet egy F átviteli függvényű taggal szűrjük (az ábrán szaggatottan jelölve). Ez a vázlat a folyamat és az egymáshoz kapcsolódó szervek jelátviteli tulajdonságait veszi figyelembe.
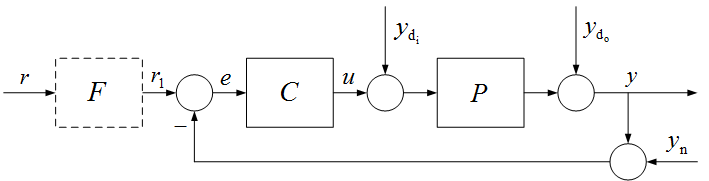
3. ábra Szabályozási kör hatásvázlata
Mivel a szabályozási körben a rendszer (folyamat, szakasz) kimenőjelét csatoljuk vissza, a szabályozás a zavarások és a mérési zaj hatásának elnyomására is alkalmas. A szabályozási körben bármilyen hatás következtében tér is el az y szabályozott jellemző a kívánt értékétől, az e rendelkezőjel (hibajel) zérustól eltérő lesz, és beavatkozójel jön létre az eltérés kiküszöbölésére.
A szabályozási struktúrában a legjobb alapjelkövetés akkor érhető el, ha a C szabályozót úgy tervezzük meg, hogy az u beavatkozójel és az r alapjel között az eredő átviteli összefüggés, a folyamat modelljének inverzét adja. Amennyiben a pontos inverz nem realizálható, annak legjobb realizálható közelítését kívánjuk megadni.
A szabályozási rendszerek a negatív visszacsatoláson alapulnak.
A szabályozási rendszer kívánt viselkedését előírásokkal adjuk meg. Ezek az előírások megadják a rendszer kívánt statikus és dinamikus viselkedését. Az előírások reálisak kell legyenek, figyelembe kell venniük a rendszer lehetőségeit és korlátait.
A C szabályozót a rendszer P modelljéhez tervezzük a minőségi előírások teljesítésére. A szabályozó u kimenőjele a beavatkozójel. A szabályozó struktúráját meg kell választani, és a szabályozóban szereplő paraméterek értékeit megfelelően kell hangolni.
A szabályozási rendszernek megfelelően kell működnie akkor is, ha a rendszer és modellje között eltérés van (illesztetlenség). A nemlinearitások hatását szintén figyelembe kell venni.
A negatív visszacsatolás nemcsak a műszaki rendszerekben lényeges. Biológiai, gazdasági, szociális, stb. rendszereknél is fontos érzékelni a kimenetet, azt visszacsatolva összehasonlítani a kívánt viselkedéssel, és az eltérés alapján beavatkozni a folyamatba. A beavatkozás a rendszer jellegétől függően egy fizikai, biológiai, stb. hatás, vagy pl. egy gazdasági utasítás.
A visszacsatolásnak rendkívül kedvező hatásai vannak a rendszer működésére.
A negatívan visszacsatolt kör alapvető tulajdonságainak szemléltetése
A szabályozási kör alapvető tulajdonságait néhány egyszerű példán szemléltetjük.
Stabilitás. A szabályozástól megkívánjuk, hogy véges bemenőjel változásra véges kimenőjel változással válaszoljon, vagyis álljon be egy állandósult állapot. A negatívan visszacsatolt szabályozási körben felléphetnek állandó vagy egyre növekvő amplitúdójú lengések. A jelenség oka, hogy a beavatkozási döntés végrehajtását a folyamat dinamikája késlelteti. A szabályozási körben lévő nagy erősítések pedig oly mértékben növelhetik a jelek kedvezőtlen tehetetlen változását, hogy a szabályozás nem lesz képes egy állandósult érték elérésére. A szabályozó struktúráját és paramétereit úgy kell megválasztani, hogy a szabályozás működése stabilis legyen.
Tekintsük példaként a 4. ábrán látható szabályozási kört. A folyamat holtidős szakasz, amelyet átmeneti függvényével (egységugrásra adott válaszával) adunk meg. A szabályozó arányos tag. Vizsgáljuk a szabályozás viselkedését egységugrás alapjelre, ha K=0.5; 1 illetve 2. A jelek alakulása könnyen követhető. Az 5. ábra a kimenőjel és a rendelkezőjel alakulását mutatja. K=0.5 mellett a szabályozás stabilis, de igen pontatlan, a kimenőjel 1 helyett 1/3 értékre áll be. K=1 esetén állandósult lengések lépnek fel, a rendszer a stabilitás határhelyzetébe került. K=2 esetén a rendszer labilis működésű. A stabilitás és a statikus, állandósult állapotbeli pontosság rendszerint ellentmondó követelmények.
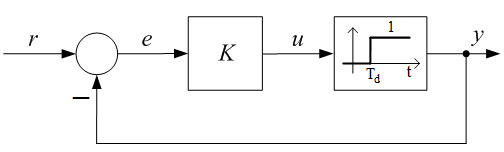
4. ábra Holtidős szabályozási kör
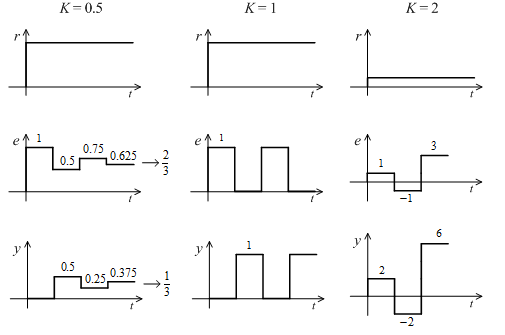
5. ábra Holtidős szabályozási kör jelei
Alapjelkövetés. A negatív visszacsatolással megvalósított szabályozással az alapjelet szeretnénk minél pontosabban követni. A 6. ábrán látható szabályozási körben a szakasz egytárolós arányos tag, a szabályozó pedig arányos tag. Ha egységugrás alapjelet kívánunk követni, a rendszerben állandósult hiba fog fellépni, mivel csak egy állandó bemenőjel képes állandó kimenőjelet létrehozni az egytárolós arányos tag kimenetén.
Az állandósult hiba nagysága. $e_{all} =\frac{1}{1+A_{P} A} $. Értéke annál kisebb, minél nagyobb az $A_{P} A$ ún. hurokerősítés vagy körerősítés. Az állandósult állapotbeli statikus pontosság biztosítható, ha az arányos szabályozó helyett integráló szabályozót alkalmazunk. Ugyanis az integrátor kimenete akkor állandósul, ha bemenőjele (az e rendelkezőjel) állandósult állapotban végülis zérusra áll be.
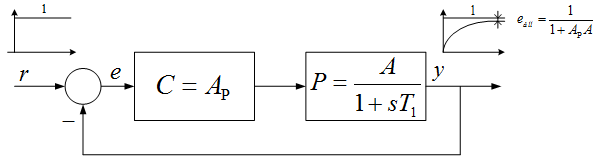
6. ábra A negatív visszacsatolás alapjelkövetésének szemléltetése
A zavarás hatásának csökkentése a kimenőjelben. A 7. ábrán látható nyitott körben a zavarás teljes egészében megjelenik a kimeneten. A negatívan visszacsatolt körben a zavarás hatása $\frac{1}{1+A \beta } $, vagyis a visszacsatolás annál jobban csökkenti a zavarás hatását, minél nagyobb az $A \beta $ hurokerősítés értéke.
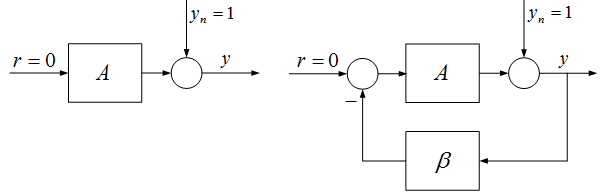
7. ábra A negatív visszacsatolás csökkenti a zavarás hatását a kimeneten
A visszacsatolás javíthatja a tranziens viselkedést. Tekintsük a 8. ábrán látható egytárolós arányos tagot.
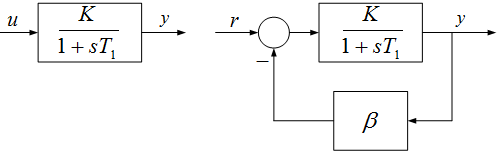
8. ábra A visszacsatolás javíthatja a tranziens viselkedést
A konstans $\beta$ visszacsatolással az eredő átviteli függvény:
$T\left(s\right)=\frac{y\left(s\right)}{r\left(s\right)} =\frac{K}{1+\beta K} \frac{1}{1+s\frac{T_{1} }{1+\beta K} } $
Az időállandó lecsökkent, tehát gyorsabb a rendszer viselkedése. Ugyanakkor az átviteli tényező is lecsökkent, amit általában kompenzálni kell.
A visszacsatolás csökkenti a folyamat érzékenységét a paraméterváltozásokra.
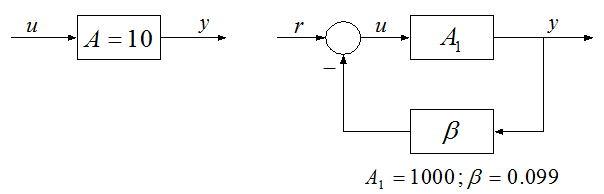
9. ábra A visszacsatolás csökkenti a rendszer érzékenységét a paraméterváltozásokra
A 9. ábrán a visszacsatolás nélkül az arányos tag átviteli tényezője 10. A visszacsatolt kör átviteli tényezője legyen ugyanennyi.
$\frac{A_{{} 1} }{1+A_{{} 1} \beta } =10$
Válasszuk $A_1$ értékét 1000-re. Ezzel $\beta = 0.099$. Ha a bemenőjel értéke 10, mindkét rendszerben a kimenőjel értéke 100. Csökkenjen az $A$ illetve az $A_1$ átviteli tényező értéke 2%-kal: $A=9.8$ és $A_1=980$. A kimenőjel értéke az eredeti rendszerben ekkor 98, míg a visszacsatolt rendszerben 99.98. A visszacsatolt körben a paraméterváltozás miatt fellépő hiba a visszacsatolás nélküli kör hibájának $(1+A_1\beta)$ -adrésze.
A nagy erősítések tartományában a visszacsatolás a visszacsatoló tag közelítő inverzét képezi.
Tekintsük a 10. ábrán látható kapcsolást. A $H_{1} (s)$átviteli tagot a $H_{2} (s)$ átviteli tagon keresztül csatoljuk vissza negatívan.
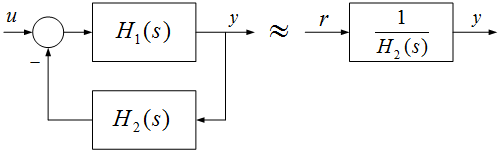
10. ábra A nagy erősítések tartományában a visszacsatolás a visszacsatoló tag közelítő inverzét képezi
Az eredő átviteli függvény: $H\left(s\right)=\frac{H_{1} \left(s\right)}{1+H_{1} \left(s\right)H_{2} \left(s\right)} $. Az eredő frekvenciafüggvényt tekintve abban a frekvenciatartományban, ahol $\left|H_{1} \left(j\omega \right)H_{2} \left(j\omega \right)\right|$ sokkal nagyobb 1-nél, az eredő a $H_{2} $ átviteli tag inverzét közelíti, $H\left(s\right)\approx \frac{1}{H_{2} \left(s\right)} $. Ahol a nyitott kör frekvenciafüggvényének abszolút értéke 1-nél sokkal kisebb, az eredő az előrevezető ág $H_{1} $ frekvenciafüggvényének menetét közelíti.
A visszacsatolásnak linearizáló hatása van. Tekintsük a 11. ábrán látható statikus nemlineáris karakterisztikát.
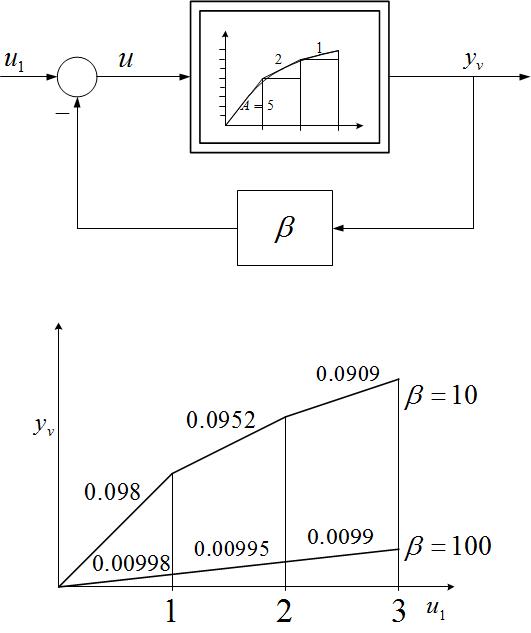
11. ábra A visszacsatolásnak linearizáló hatása van
A statikus karakterisztika három linearizált tartományra osztható, ahol az arányos átviteli tényezőt az adott munkaponthoz illesztett egyenes $A$ meredeksége adja meg. Az arányos visszacsatolás értéke legyen $\beta $. A visszacsatolt körben az egyes tartományokban a meredekség, vagyis a visszacsatolt linearizált részrendszer átviteli tényezője $\frac{A_{{} } }{1+A\beta } $ . Minél nagyobb az $A\beta$ tényező értéke, annál jobban megközelíti az átviteli tényező az $1/\beta$ értéket, és függetlenné válik az egyes szakaszok $A$ meredekségétől. A 11. ábrán feltüntettük a visszacsatolt részrendszerek átviteli tényezőit $\beta=10$ és $\beta=100$ esetére. Látható, hogy az egyes résztartományok meredeksége közel azonos, a karakterisztika közel lineáris az egész tartományra.
Hivatkozások:
Keviczky, Bars, Hetthéssy, Barta, Bányász: Szabályozástechnika, 2009, Műegyetemi Kiadó, 55079. This chapter is based on this university lecture notes. With the permission of the authors.
Kokotović, P.V. The Joy of Feedback: Nonlinear and Adaptive. 1991 Bode Prize Lecture, IEEE Control Systems Magazine, 3: 7-17, 1992.
Åström, K.J., Murray, R.M. Feedback Systems: An Introduction for Scientists and Engineers. Princeton University Press, 2008.