
Nemlineáris rendszerek szakaszonkénti linearizálása
Folytonos idejű lineáris időinvariáns (LTI) rendszerek
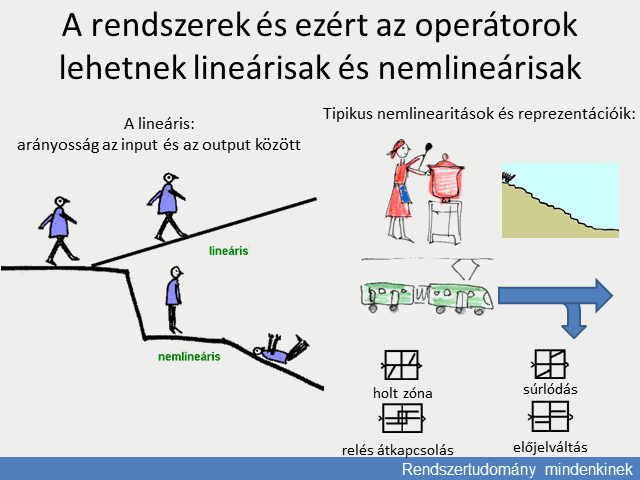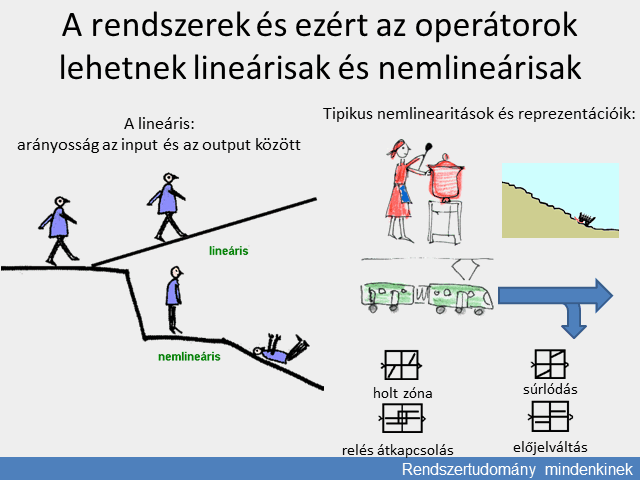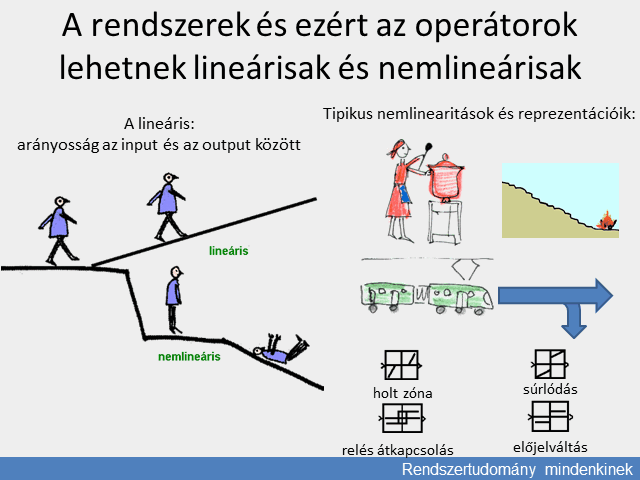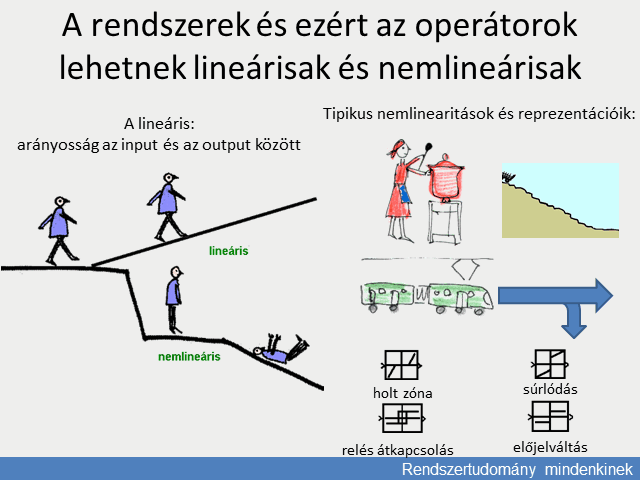
A természeti jelenségek általában nemlineárisak. A kimenőjel és a bemenőjel állandósult értékeinek kapcsolata egy ún. statikus karakterisztikával adható meg, amely rendszerint nem egyenes. Például ha egy árammal átjárt tekercs fluxusának és áramának kapcsolatát tekintjük, a mágnesezési jelleggörbe a kis áramok tartományában lineáris, a fluxus arányos az árammal, azonban nagy áramoknál a mágnesezési görbe telítődik, nemlineárissá válik. (Itt a hiszterézis jelensége is fellép, a statikus görbe kétértékű lesz, a felmágnesezés és lemágnesezés nem ugyanazon görbe mentén játszódik le.) A következőkben tekintsünk egy egyértékű statikus karakterisztikát.
Az 1. ábra egy nemlineáris statikus karakterisztikát mutat.
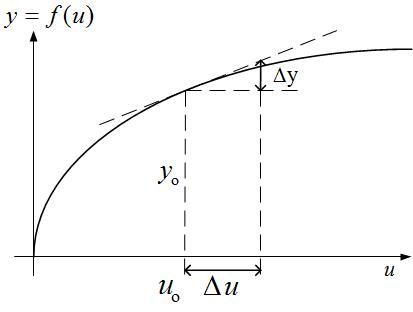
- ábra Statikus karakterisztika
A lineáris rendszerek vizsgálatára jól kidolgozott általános módszerek állnak rendelkezésre. A lineáris rendszerekre érvényes a szuperpozíció elve. Ha a rendszerre több bemenőjel hat, külön-külön vizsgálható a kimenőjel alakulása az egyes bemenőjelek hatására, majd ezek a hatások a kimenőjelre összegezhetők.
A nemlineáris rendszerek vizsgálata nehéz feladat. Nincsenek általános módszerek, az egyes nemlineáris rendszerek külön tanulmányozandók.
A vizsgálat leegyszerűsíthető, ha a nemlineáris statikus karakterisztikát egy adott munkapont környezetében linearizáljuk. Ily módon a munkapont közelében a bemenőjelek kis megváltozására lineáris modellel közelítjük a nemlineáris rendszert.
A statikus karakterisztika linearizálása
Tekintsük az 1. ábrán látható $y=f\left(u\right)$ statikus nemlineáris karakterisztikát.
Az $u=u_{0} $ munkapontban a függvény Taylor sora:
$y=y_{0} +\Delta y=f\left(u_{0} \right)+f^{'} \left(u_{0} \right)\left(u-u_{0} \right)+...$
$f^{'} \left(u_{0} \right)$ az f függvény u szerinti deriváltját jelenti az $u_{0} $ munkapontban.
A magasabb hatványú tagokat elhanyagolva a linearizált modell
$y-y_{0} =\Delta y=f^{'} \left(u_{0} \right)\left(u-u_{0} \right)=f^{'} \left(u_{0} \right)\Delta u$
A linearizált modell a statikus karakterisztikát a munkapontban az érintővel helyettesíti. Természetesen a meredekség munkapontfüggő.
Linearizálás több bemenő változó esetén
Legyen az y kimenőjel az $u=\left(u_{1} ,u_{2} ,...,u_{n} \right)$ bemenő változók függvénye. Az y jel tehát skalár-vektor függvény. A munkapontot jelölje az $u_{0} =\left(u_{10} ,u_{20} ,...,u_{n0} \right)$ vektor. A munkapont kis környezetében a kimenőjel értéke Taylor sorfejtéssel közelítően meghatározható.
$y=y_{0} +\Delta y=f\left(u_{0} \right)+\sum _{i=1}^{n}\left. \frac{\partial f\left(u\right)}{\partial u_{i} } \right|_{u_{0} } \left(u_{i} -u_{i0} \right) +...$
A másod- és magasabbrendű deriváltakat elhanyagolva az függvény munkapont körüli kis megváltozása lineáris összefüggéssel adható meg:
$\Delta y=\sum _{i=1}^{n}A_{i} \Delta u_{i} $
A linearizált vázlatot a 2. ábra szemlélteti. Az $A_{i} $ tényezők a linearizált modell ún. statikus átviteli tényezői, amelyek értékei munkapontfüggők.
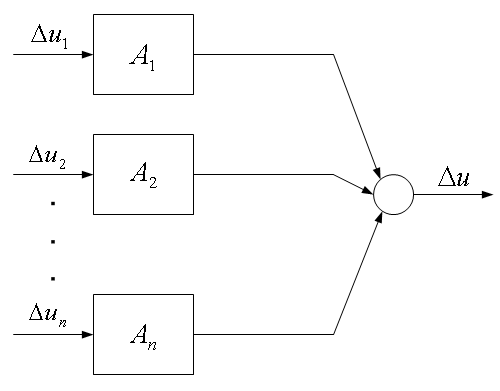
2. ábra Több bemenetű - egy kimenetű statikus karakterisztika linearizálása
Ha a lineáris vagy linearizált modellek paraméterei nem változnak, állandó paraméterű (időinvariáns, LTI – linear time invariant) lineáris rendszerekről beszélünk.
A statikus viselkedés mellett a rendszerek dinamikus mozgását is vizsgálnunk kell, vagyis azt, hogyan jut el a rendszer az egyik statikus állapotból a másikba. Az időbeli változást a rendszer felépítése, alkotóelemeinek kapcsolódása, paramétereinek értéke, tehát a rendszer modellje befolyásolja.
Az LTI lineáris időinvariáns rendszereket leírhatjuk bemeneti-kimeneti (input-output) modellekkel vagy állapotmodellekkel.
A bemeneti-kimeneti modellek az y kimenőjel és az u bemenőjel között írják le a kapcsolatot, amely rendszerint egy n-edrendű differenciálegyenlettel adható meg. A differenciálegyenlet a kimenőjel és annak kis megváltozásai (differenciálhányadosai) és a bemenőjel és annak kis megváltozásai közötti kapcsolatot írja le.
A rendszernek vannak belső változói, ún. állapotváltozói is. Az állapotváltozókra jellemző, hogy pillanatnyi értéküket a rendszerben a múltban bekövetkezett változások alakították ki, és a bemenőjel hirtelen változására nem képesek hirtelen változásokkal válaszolni, a bemenőjel által meghatározott új értéküket fokozatosan érik el. Úgy is mondhatjuk, hogy az állapotváltozóknak „memória” tulajdonságuk van, pillanatnyi értékükben tárolják a rendszerben bekövetkezett múltbeli mozgások hatását. Ilyen állapotváltozók például mechanikai rendszerekben az elmozdulás, a sebesség, villamos rendszerekben az áram, a töltés.
A rendszer kimenőjele általában az állapotváltozókon keresztül alakul ki.
A bemenőjelet, a kimenőjelet és az állapotváltozókat a rendszerben a 3. ábra szemlélteti.
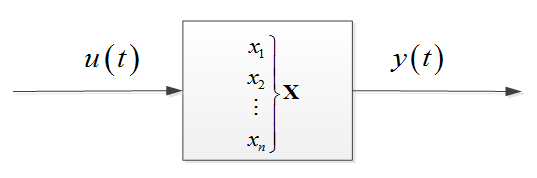
3. ábra A rendszer jelei a bemenőjel, a kimenőjel és a belső állapotváltozók
Az állapotváltozókkal a rendszer viselkedése elsőrendű differenciálegyenletek rendszerével írható fel. Az állapotváltozós leírás előnye, hogy nemcsak a rendszer kimenőjelét adja meg, hanem információt nyerünk a rendszer belső állapotváltozóinak időbeli alakulásáról is. Az elsőrendű differenciálegyenlet-rendszer megoldása egyszerűbb, mint az n-edrendű differenciálegyenlet megoldása. A megoldás mindkét leírási forma esetén egyszerűsödik, ha olyan egyszerű, de a gyakorlat szempontjából jellemző egyszerű bemenőjeleket veszünk figyelembe, mint például az ugrásalakú gerjesztés.
A Rendszer és modellje fejezetben (31. tábla) példát mutattunk be egy ellenállásból, induktivitásból és kapacitásból álló villamos áramkör és egy tömegből, rugóból és viszkóz csillapításból felépülő mechanikai rendszer differenciálegyenletének és állapotegyenletének megadására. Az egyenletek megadott kezdeti feltételekre és megadott bemenőjelre (gerjesztésre) való megoldása megadja a rendszer dinamikus viselkedését, azaz hogyan jut el a rendszer a kezdeti állapotából a végállapotába.