

Napjaink gyakorlatára egyre inkább jellemző, hogy az irányítási rendszereket megfelelő valós idejű (real-time) szolgáltatásokkal is rendelkező digitális berendezések valósítják meg. Attól függően, hogy egy adott alkalmazáson belül hány és milyen bonyolultságú szabályozási kör feladatát kell ellátni, a digitális irányító berendezések köre az egyetlen chip-ből álló mikrokontrollerektől a nagyobb teljesítményű midi/mini digitális számítógépekig terjed. A digitális berendezések hálózatba szervezésének fejlettsége lehetővé teszi elosztott irányítási rendszerek létrehozását is.
A számítógépes folyamatirányításnál a folytonos folyamat szabályozásának alapvető feladatait a számítógép végzi el valós időben. A kimenőjelet a számítógépes feldolgozáshoz digitalizálni kell. Adott mintavételi időközönként a folytonos jelből mintát veszünk, amelyhez kvantálás és digitalizálás után számértéket rendelünk, amit a számítógép fogadni tud. Ezeket a műveleteket az A/D analóg/digitális átalakító végzi. Ezen keresztül csatlakoztatjuk a folytonos folyamatot a számítógéphez. A számítógépben mintavételi időközönként ún. „task”-ok futnak le, amelyek zárthurkú szabályozás megvalósításakor digitális alapjelet képeznek, fogadják a jelet a folyamat felől és esetleg szűrik is, összehasonlítják az alapjelet a mért kimenőjel értékével, majd a hibajel alapján valamilyen diszkrét szabályozási algoritmus alapján képezik a beavatkozójelet. A diszkrét szabályozási algoritmust egy program realizálja. Ezután a beavatkozójelet a számítógép kiadja a folyamatra. Ez digitális jel, amelyet analóg jellé kell alakítani, számértékből olyan fizikai jelet kell létrehozni, amely a beavatkozószervet működtetni tudja (pl. feszültség, szelepszár pozícióhelyzete, stb.). Ezt a műveletet a D/A digitális/analóg átalakító végzi, amely a számítógépet a folytonos folyamattal köti össze. Gondoskodni kell arról is, hogy a beavatkozójel bemenőjele a mintavételi pontok között is rendelkezésre álljon. Ezt ún. tartószervvel biztosítjuk, amely a leggyakrabban tartja az előző jel értékét, amíg a következő mintavételi pontban nem jön be az újabb jel (zérusrendű tartószerv, ZOH, zero order hold).
A mintavételes szabályozási kör felépítését az 1. ábra szemlélteti. A zérusrendű tartószervvel a folytonos idejű jel mintavételezésével és tartásával előálló jelet a 2. ábra mutatja (a mintavételezési időt Ts-sel jelöljük). Látható, hogy ha a lépcsős jelet közelítjük egy folytonos jellel, az körülbelül egy fél mintavételi idővel késik az eredeti folytonos jelhez képest.
A digitális technológia előnyei az analóg szabályozásokkal összehasonlítva: megbízhatóbb és olcsóbb, különböző szabályozási algoritmusok valósíthatók meg megfelelő programozással, a szabályozás paramétereinek megváltoztatására, a működés monitorozására egyszerű és hatékony módszerek állnak rendelkezésre.
A mintavételes szabályozásokat, amelyekben a folytonos szabályozásokhoz hasonlóan negatív visszacsatolás valósul meg, a későbbiekben kissé részletesebben is tárgyaljuk.
1.ábra Mintavételes szabályozási kör felépítése
2. ábra Zérusrendű tartószerv alkalmazása (mintavételezés és tartás)
A mintavételezési időt gondosan kell megválasztani: egyrészt összhangban kell lennie az irányítandó folyamat dinamikájával, másrészt a real-time (valós idejű) feldolgozó rendszer képességeivel (műveletvégző sebesség, számábrázolás pontossága). A mintavételezési frekvencia legalább kétszerese kell legyen a jelben lévő legmagasabb frekvenciájú összetevő frekvenciájánál (Shannon mintavételezési tétel). Az időtartományban ez azt jelenti, hogy egy lengő jel minden félperiódusában legalább egy mintát kell venni, hogy a mintavételezett információból következtetni tudjunk a folytonos jel lefolyására. Minél kisebb a mintavételezési idő, annál inkább megközelíti a szabályozási rendszer működése a folytonos működést. Nagyobb mintavételi idővel kevesebb számítást kell végezni. A mintavételi idő megválasztásával befolyásolhatjuk a szabályozás dinamikáját, gyorsaságát, a beavatkozójel nagyságát.
A mintavételezett rendszerek viselkedésének vizsgálatához a mintavételezett jelek és a mintavételezett jelekkel gerjesztett rendszerek matematikai leírását tárgyaljuk.
Jelölje y(t) a folytonos jelet, $y[k]=y\left(kT_{s} \right)$ pedig a diszkrét idejű jel mintavételezett értékeit, ahol $T_{s} $ a mintavételezési időt, $k=0,1,2,...$ pedig a mintavételezés sorszámát jelöli.
Egy folytonos jel digitális alakját eltolt impulzusok összegével lehet leírni.
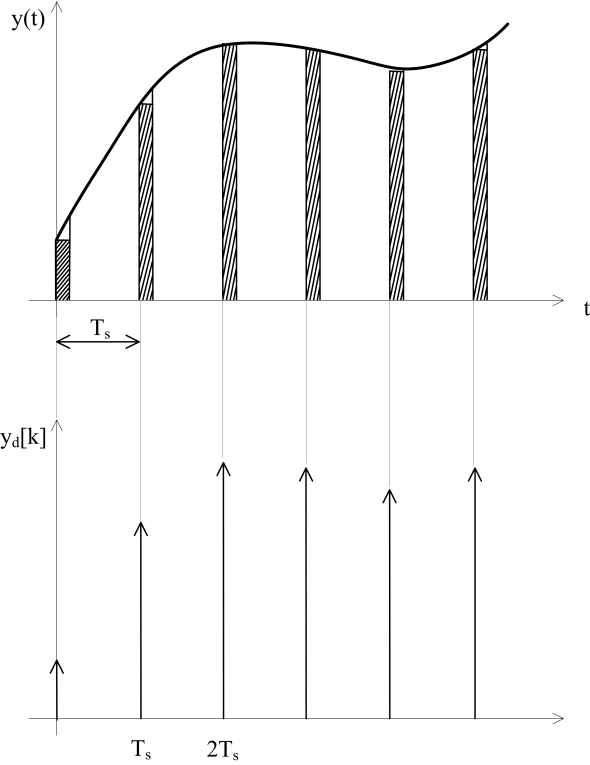
3. ábra Fizikai és matematikai mintavételezés
A 3. ábra a fizikai és a matematikai mintavételezést szemlélteti. A jelből mintavételi időközönként mintát veszünk, A kapcsoló rövid ideig tart zárva. A jeleket négyszögimpulzusokkal közelítjük. A matematikai mintavételezésnél a négyszögimpulzusokat Dirac delta impulzusokkal helyettesítjük, amelyek amplitúdója azonos az impulzus területével, illetve arányos az impulzusok amplitúdójával.
A mintavételezett jel az időtartományban az eltolt impulzusok összegével írható le.
$$y_{{\rm d}} \left[k\right]=y\left(t=kT_{{\rm s}} \right)=y\left(0\right)\delta \left(t\right)+y\left(T_{{\rm s}} \right)\delta \left(t-T_{{\rm s}} \right)+y\left(2T_{{\rm s}} \right)\delta \left(t-2T_{{\rm s}} \right)+y\left(3T_{{\rm s}} \right)\delta \left(t-3T_{{\rm s}} \right)+...$$
Az $y\left(t=kT_{{\rm s}} \right)=y_{{\rm d}} \left[k\right]$ jel Laplace transzformáltja:
$Y_{d}(s)=y(0)+y(T_{s})e^{-sT_{s}}+y(2T_{s})e^{-2sT_{s}}+y(3T_{s})e^{-3sT_{s}}+\dots$
Vezessük be a $z=e^{sT_{{\rm s}} } $ és $z^{-1} =e^{-sT_{{\rm s}} } $ jelöléseket.
$ z=e^{sT_{{\rm s}} } $ a z-transzformált, $ z^{-1} $ pedig az eltolási operátor.
A z-transzformáció az s komplex számsíkot egy másik komplex számsíkba képezi le a fenti összefüggés szerint. Az s sík imaginárius tengelye az egységsugarú körbe képződik le. A bal oldali félsík a kör belsejébe, a jobb oldali félsík a kör külsejébe képződik le (4. ábra).
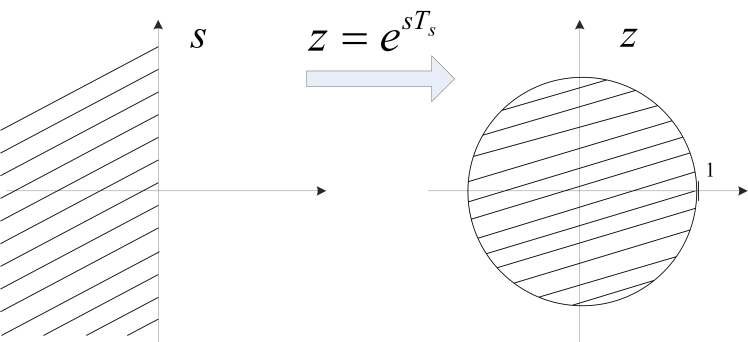
4. ábra A z-transzformáció az s komplex síkot a z komplex síkba képezi le
Mivel a teljes bal oldali félsík a leképezéskor az egységsugarú kör belsejébe „zsugorodik”, az egyes pontok megadásakor a z-tartományban nagyobb pontosságra van szükség, mint az s-tartományban.
A fenti jelölésekkel az $y_{{\rm d}} \left[k\right]$ mintavételezett jel z-transzformáltja:
$Y_{{\rm d}} \left(z\right)=y\left(0\right)+y\left(T_{{\rm s}} \right)z^{-1} +y\left(2T_{{\rm s}} \right)z^{-2} +y\left(3T_{{\rm s}} \right)z^{-3} +...=\sum _{k=0}^{\infty }y\left(kT_{{\rm s}} \right)z^{-k} $
A jel z-transzformáltja az eltolási operátorral kifejezve megadja az egyes mintavételi pontokban a jel értékét.
Néhány tipikus jel z-transzformáltja
Származtassuk néhány elemi diszkrét idejű függvény z-transzformáltját.
Az f [k] mintavételezett jel z-transzformáltját sokszor a $Z\left\{f[k]\right\}=F\left(z\right)$ jelöléssel adjuk meg.
Egységimpulzus (Dirac delta):$f[k]\equiv 1,{\rm \; \; \; k=0}$ , egyébként $f[k]\equiv {\rm 0}$
A jel a t = 0 időpillanatban végtelen amplitúdójú impulzus, amelynek területe egységnyi. A jelet az 5. ábra mutatja. Olyan négyszögimpulzus határértékének tekinthető, amelynek időtartama egyre csökken, amplitúdója pedig egyre nő.
5. ábra Egységimpulzus (Dirac delta)
$Z\left\{f[k]\right\}=\sum _{k=0}^{\infty }z^{-k} f[k]=1+\sum _{k=1}^{\infty }z^{-k} \cdot 0=1$
Egységugrás: $f[k]\equiv 1,{\rm \; \; \; k=0,1,2,...}$
6. ábra Egységugrás és mintavételezett értékei
Alkalmazzuk a geometriai sor összegképletét, ekkor a $\left|z\right|>1$ konvergencia tartomány mellett:
$Z\left\{f[k]\right\}=\sum _{k=0}^{\infty }z^{-k} f[k]=\sum _{k=0}^{\infty }z^{-k} \cdot 1={1\over 1-z^{-1} } ={z\over z-1} $
Exponenciális függvény: $f[k]\equiv e^{-akT_{s} } ,{\rm \; \; \; k=0,1,2,...}$
A folytonos jelet és mintavételezett értékeit nyíllal jelölve a 7. ábra szemlélteti.
7. ábra Folytonos és mintavételezett exponenciális jel
A hatványfüggvényre származtatott összefüggést felhasználva a $\left|z\right|>\left|e^{-aT_{s} } \right|$ konvergencia tartomány mellett:
$Z\left\{f[k]\right\}=\sum _{k=0}^{\infty }z^{-k} f[k]=\sum _{k=0}^{\infty }z^{-k} e^{-akT_{s} } ={1\over 1-e^{-aT_{s} } z^{-1} } ={z\over z-e^{-aT_{s} } } $
A különböző jelek z-transzformáltjaira táblázatok állnak rendelkezésre.
A jelek z változóval felírt z-transzformáltjából az inverz z-transzformációval kaphatjuk meg a jel értékeit az egyes mintavételi időpontokban. Ennek egyik módja a polinomosztás, a jel a z-transzformáltja számláló és nevező polinomjainak osztásával megkapjuk a jel z-transzformáltját az eltolási operátorral kifejezve, amelyből a jel értékei az egyes mintavételi pontokban megadhatók.
Egy folytonos folyamatot a D/A átalakítóval együtt az impulzusátviteli fügvénnyel írhatjuk le. Az impulzusátviteli függvény a kimenőjel és a bemenőjel z-transzformáltjainak hányadosát adja meg zérusrendű tartószervet feltételezve a bemeneten (8. ábra).
8. ábra Az impulzusátviteli függvény értelmezése
Az u(t) tartott bemenőjelet és az y[k] mintavételezett jeleket a 9. ábra szemlélteti.
9. ábra A folyamat tartott bemenőjele és mintavételezett kimenőjele
A diszkretizált rendszert leíró impulzusátviteli függvény
$G\left(z\right)={Z\left\{y[k]\right\}\over Z\left\{u[k]\right\}} ={Y\left(z\right)\over U\left(z\right)} $
amely a rendszer átmeneti függvényének (egységugrás válaszának) ismeretében az alábbi összefüggéssel is számítható:
$G\left(z\right)={Z\left\{v[k]\right\}\over Z\left\{u[k]\right\}} ={Z\left\{v[k]\right\}\over {z\over z-1} } ={z-1\over z} Z\left\{v[k]\right\}=\left(1-z^{-1} \right)Z\left\{v[k]\right\}$
Ha ismerjük az impulzusátviteli függvényt és a bemenőjel z-transzformáltját, a kimenőjel z-transzformáltja kiszámítható.
Néhány tipikus rendszer (tag) impulzusátviteli függvénye
Az impulzusátviteli függvények meghatározásához tételezzünk fel a rendszer bemenetén Dirac delta vagy egységugrás bemenőjelet, amelyek z-transzformáltját ismerjük. Szemléltetésképpen kövessük a rendszerben a jel útját, és határozzuk meg a kimenőjel z-transzformáltját, majd az impulzusátviteli függvényt.
Holtidős tag
A mintavételezett rendszer vázlatát a 10. ábra mutatja.

10. ábra Holtidős tag mintavételezése
Legyen a Td holtidő és a Ts mintavételezési idő hányadosa a k egész szám. A kimenőjel k lépéssel késik a bemenőjelhez képest. A holtidős tag impulzusátviteli függvénye:
$G\left(z\right)=z^{-k} $
Integráló tag
A rendszer vázlatát a 11. ábra adja meg.

11. ábra Integráló tag mintavételezése
A folytonos tag átviteli függvénye: $P\left(s\right)=1/s$. Gerjesszük most a rendszert Dirac delta bemenőjellel, amelynek z-transzformáltja $U\left(z\right)=1$. A zérusrendű tartószerv kimenetén egységnyi amplitúdójú, Ts ideig tartó négyszögimpulzus jelenik meg, amelynek hatására az integrátor kimenetén lineárisan növekvő, majd Ts értéken állandósuló jel jelenik meg. A mintavételezett kimenőjel z-transzformáltja:
$Y\left(z\right)=0+T_{{\rm s}} {\kern 1pt} z^{-1} +T_{{\rm s}} z^{-2} +T_{{\rm s}} z^{-3} +...=T_{s} z^{-1} \left(1+z^{-1} +z^{-2} +...\right)={T_{s} {\kern 1pt} z^{-1} \over 1-z^{-1} } ={T_{s} \over z-1} $
és az impulzusátviteli függvény:
$G\left(z\right)={Y\left(z\right)\over U\left(z\right)} ={T_{s} \over z-1} $
Megjegyezzük, hogy a folytonos tag pólusa (az átviteli függvény nevezőjének zérushelye) az s tartományban: $s_{1} =0$, a mintavételezett rendszer pólusa pedig a z tartományban:$z_{1} =1$ .
Egytárolós arányos tag
A rendszer vázlatát a 12. ábra adja meg.

12. ábra Egytárolós arányos tag mintavételezése
A folytonos tag átviteli függvénye:
$P\left(s\right)={1\over 1+sT_{1} } . $
Gerjesszük a rendszert mintavételezett egységugrással, amelynek z-transzformáltja
$U\left(z\right)={z\over z-1} .$
A folytonos kimenőjel az egytárolós arányos tag egységugrásra adott válasza:
$y\left(t\right)=1-e^{-t/T_{s} } $
Az ebből képzett mintavételezett jelsorozat z-transzformáltja:
$Y\left(z\right)=0+\left(1-e^{-T_{s} /T_{1} } \right)z^{-1} +\left(1-e^{-2T_{s} /T_{1} } \right)z^{-2} +\left(1-e^{-3T_{s} /T_{1} } \right)z^{-3} +...$
A kimenőjel és a bemenőjel z-transzformáltjait elosztva kapjuk a tag impulzusátviteli függvényét:
$G\left(z\right)={Y\left(z\right)\over U\left(z\right)} ={1-e^{-T_{s} /T_{1} } \over z-e^{-T_{s} /T_{1} } } $
A folytonos tag pólusa $s_{1} =-1/T_{1} $ a z-tartományban a $z_{1} =e^{-T_{s} /T_{1} } $ pontba képződik le.
Összekapcsolt tagok eredő impulzusátviteli függvényei
Ha tagokat úgy kapcsolunk össze, hogy közöttük mintavételező és tartószerv van, akkor az eredő impulzusátviteli függvényeket ugyanúgy számoljuk, mint a folytonos rendszereknél, soros kapcsolásnál az eredő az impulzusátviteli függvények szorzata, párhuzamos kapcsolásnál az eredő az impulzusátviteli függvények összege.
Többtárolós arányos tag
Ha többtárolós tagokról van szó, vagyis a folytonos átviteli függvény több egytárolós tag szorzatából áll és az egyes tárolós tagok között nincs mintavételező és tartószerv, az impulzusátviteli függvényt az eredeti definíció szerint kell származtatni.
A számítást egyszerűsíthetjük, ha az átviteli függvényt részlettörtekre bontjuk és a részlettörtekre meghatározott impulzusátviteli függvényeket összegezzük.
Kéttárolós arányos tagra az eljárást a 13. ábra szemlélteti.
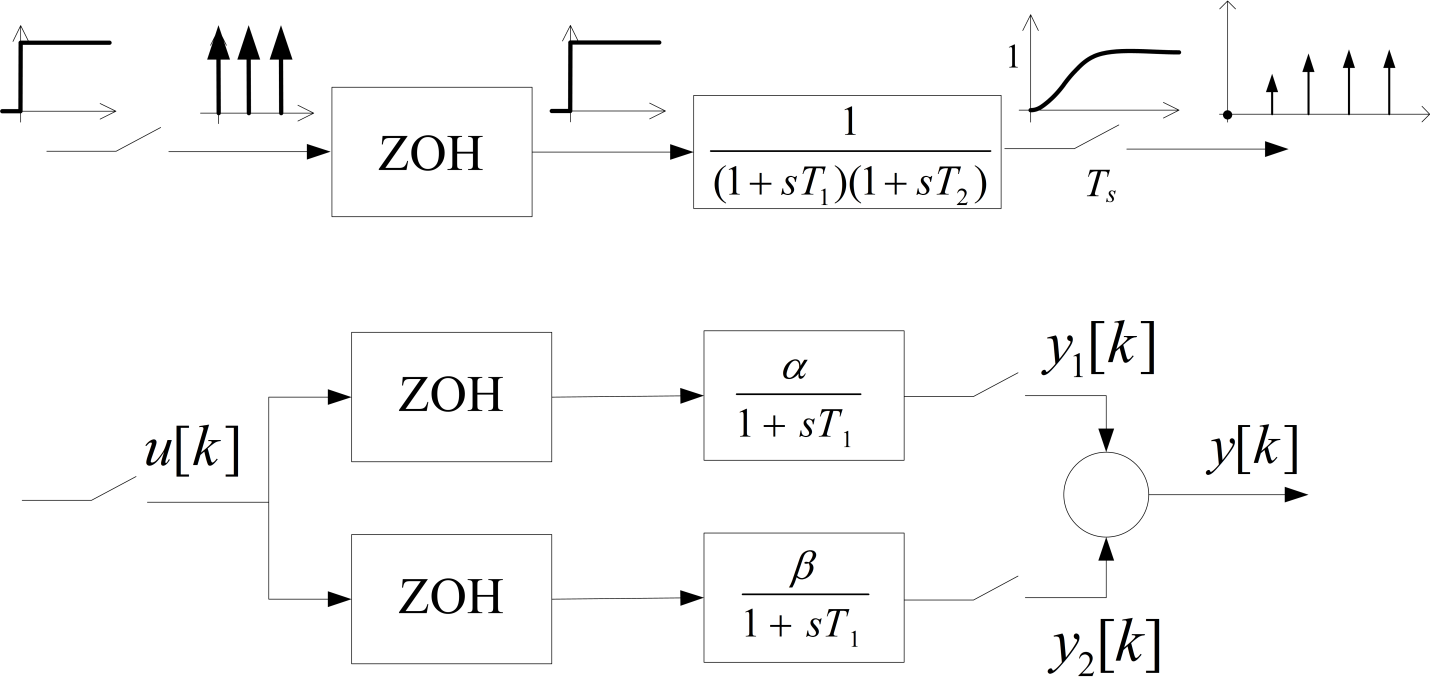
13. ábra Kéttárolós arányos tag mintavételezése
Az impulzusátviteli függvény:
$G\left(z\right)={Y\left(z\right)\over U\left(z\right)} =\alpha {1-e^{-T_{s} /T_{1} } \over z-e^{-T_{s} /T_{1} } } +\beta {1-e^{-T_{s} /T_{1} } \over z-e^{-T_{s} /T_{1} } } ={\delta \left(z+\sigma \right)\over \left(z-e^{-T_{s} /T_{1} } \right)\left(z-e^{-T_{s} /T_{1} } \right)} $
A mintavételezés következtében létrejött egy zérus is, holott a folytonos rendszer átviteli függvényében nem szerepelt zérus. Az impulzusátviteli függvény pólus-zérus konfigurációját a 14. ábra mutatja.
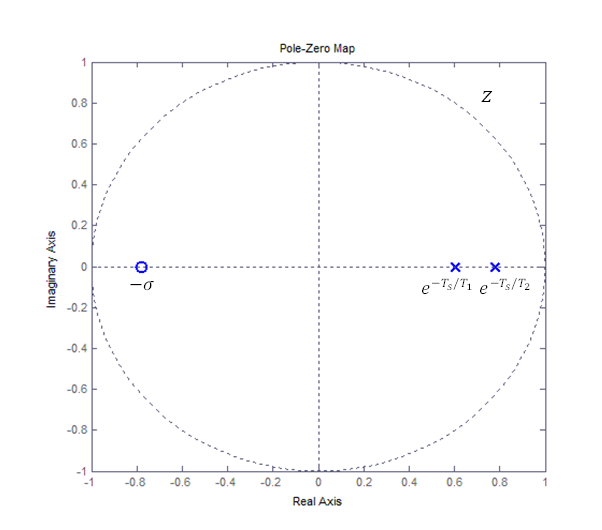
14. ábra Mintavételezett kéttárolós arányos tag impulzusátviteli függvényének pólus-zérus konfigurációja
Példaként tekintsük a $P\left(s\right)={1\over \left(1+5s\right)\left(1+10s\right)} $ átviteli függvénnyel adott kéttárolós arányos tagot. $T_{{\rm s}} =2.5$ mintavételezési idővel az impulzusátviteli függvény:
$G\left(z\right)=0.048929{\left(z+0.7788\right)\over \left(z-0.7788\right)\left(z-0.6065\right)} .$
Többtárolós arányos tagok impulzusátviteli függvényében a zérusok száma 1-gyel kevesebb a pólusok számánál. Lesznek az egységkörön kívülre eső zérusok is.
Az időtartományban a rendszer kimenőjelének aktuális értékét az adott mintavételi időpontban megadhatjuk a bemenőjel aktuális és néhány korábbi értékének, továbbá a kimenőjel néhány korábbi értékének ismeretében. Úgy is mondhatjuk, hogy a mintavételes rendszer véges memóriájú. A differenciaegyenlet rekurzív formula.
Tekintsünk példaként egy integrátort, amelynek erősítési tényezője K. A bemenőjelet két mintavételi pont között állandó értéken tartjuk (11. ábra). A kimenőjel az alábbi összefüggéssel (differenciaegyenlettel) számítható:
$y\left[k+1\right]=y\left[k\right]+KT_{s} u\left[k\right]$
A differenciaegyenlet az impulzusátviteli függvényből is származtatható.
Tekintsük az integráló tag
$G\left(z\right)={Y\left(z\right)\over U\left(z\right)} ={KT_{s} \over z-1} ={KT_{s} {\kern 1pt} z^{-1} \over 1-z^{-1} } $
impulzusátviteli függvényét. Átrendezve:
$Y\left(z\right)=Y\left(z\right)z^{-1} +KT_{s} U\left(z\right)z^{-1} $
Az időtartományban a z-1-gyel való szorzás egy mintavételi idővel korábbi jel értékét jelenti. Áttérve az időtartományra az alábbi rekurzív összefüggést kapjuk:
$y\left[k\right]=y\left[k-1\right]+KT_{s} u\left[k-1\right]$
Tehát az aktuális kimenőjel értéke a kimenőjel előző és a bemenőjel előző értékéből számítható.
A mintavételes rendszert is meg lehet adni állapotteres modelljével. Hasonlóan a folytonos rendszerekhez, több állapotreprezentáció lehetséges, miközben a kimenet és a bemenet közötti kapcsolat ugyanaz.
A diszkrét állapotegyenlet meghatározható a folytonos állapotváltozók mintavételezésével.
Induljunk ki a folytonos állapotegyenlet általános megoldásából:
$x\left(t\right)=e^{A\left(t-t_{0} \right)} x\left(0\right)+\int _{t_{0} }^{t}e^{A\left(t-\tau \right)} bu\left(\tau \right)d\tau $
A mintavételezés során alkalmazzunk zérusrendű tartószervet. Végezzük el az integrálást két egymást követő mintavételi pont között. Legyen t0 egy mintavételi intervallum kezdete, $t_{0} =kT_{{\rm s}} $, ahol $T_{{\rm s}} $ a mintavételezési idő. Az intervallum vége $t=\left(k+1\right)T_{{\rm s}} $. Ebben a tartományban $u\left(\tau \right)={\rm állandó}=u\left(kT_{{\rm s}} \right)$, és így kiemelhető az integrálás elé. Amennyiben az A mátrix invertálható, az integrálást elvégezve
$x\left[\left(k+1\right)T_{{\rm s}} \right]=e^{AT_{{\rm s}} } x\left(kT_{{\rm s}} \right)+A^{-1} \left(e^{AT_{{\rm s}} } -I\right)bu\left(kT_{{\rm s}} \right)$
Az $u\left(kT_{{\rm s}} \right)=u\left[k\right]$, $x\left[\left(k+1\right)T_{{\rm s}} \right]=x\left[k\right]$ jelöléseket alkalmazva a mintavételezett rendszer állapotegyenlete:
$\matrix{{x\left[k+1\right]=F{\kern 1pt} x\left[k\right]+g{\kern 1pt} {\kern 1pt} u\left[k\right]} \cr {y\left[k\right]=c^{{\rm T}} x\left[k\right]+d{\kern 1pt} {\kern 1pt} u\left[k\right]}}$
ahol $F=e^{AT_{{\rm s}} } ;{\rm \; \; \; }g=A^{-1} \left(e^{AT_{{\rm s}} } -I\right)b$
A diszkrét és a folytonos esetre a $c^{{\rm T}} $ és d paraméterek megegyeznek. Ismeretes, hogy a gyakorlati folyamatokra tipikusan d= 0 áll fenn.
A diszkrét állapotegyenlet különböző alakjai határozhatók meg az impulzusátviteli függvények alapján is.
Egy ún. predikciós modellel az adott k mintavételi pillanatig a bemenőjelről és az állapotváltozókról (illetve a kimenőjelről) rendelkezésre álló információ, adatok alapján kívánjuk meghatározni, prediktálni a rendszer jövőbeni kimenőjelének, illetve állapotváltozóinak értékeit. Feltételezzük, hogy a bemenőjel közvetlenül nem befolyásolja a kimenőjelet, csupán az állapotváltozókon keresztül. A jelek előrebecsült, prediktált értékeit “kalappal” jelöljük. Predikciós modellekre van szükség predikciós szabályozási algoritmusok megvalósításához, ahol a jövőbeni várható viselkedés figyelembevételével határozzuk meg a folyamat aktuális bemenőjelét. Az állapotváltozós leírásból könnyebben vezethetünk le predikciós modellt, mint az impulzusátviteli függvényből kiindulva.
$\hat{x}(\left. k+1\right|k)=F\hat{x}(k)+gu(k)$
$\hat{y}(\left. k+1\right|k)=c_{}^{T} \hat{x}(\left. k+1\right|k)$
A következő k+1, k+2,… mintavételi pontokban a jelek értékei fokozatos behelyettesítésekkel kaphatók meg:
${\hat{x}(\left. k+2\right|k)=F\hat{x}(\left. k+1\right|k)+gu(k+1)=F_{}^{2} x(k)+Fgu(k)+gu(k+1)}$
${\hat{x}(\left. k+3\right|k)=F\hat{x}(\left. k+2\right|k)+gu(k+2)=F_{}^{3} x(k)+F_{}^{2} gu(k)+Fgu(k+1)+gu(k+2)}$
${\hat{x}(\left. k+4\right|k)=F\hat{x}(\left. k+3\right|k)+gu(k+3)=F_{}^{4} x(k)+F_{}^{2} gu(k)+F^{2} gu(k+1)+Fgu(k+2)+gu(k+3)}$
$ {\vdots }$
A függőleges vonások azt jelentik, hogy a jel prediktált értékét az aktuális k időpontig rendelkezésre álló információ alapján határozzuk meg.
Vektor/mátrix alakban 4 előrejelzett pontig:
$\left[\matrix{{\hat{x}(\left. k+1\right|k)} \cr {\hat{x}(\left. k+2\right|k)} \cr {\hat{x}(\left. k+3\right|k)} \cr {\hat{x}(\left. k+4\right|k)}}\right]=\left[\matrix{{F} \cr {F^{2} } \cr {F^{3} } \cr {F^{4} }}\right]\hat{x}(k)+\left[\matrix{{g} & {0} & {0} & {0} \cr {Fg} & {g} & {0} & {0} \cr {F^{2} g} & {Fg} & {g} & {0} \cr {F^{3} g} & {F^{2} g} & {Fg} & {g}}\right]\left[\matrix{{u(k)} \cr {u(k+1)} \cr {u(k+2)} \cr {u(k+3)}}\right]$
A kimenőjelet az egyes sorok cT –vel való szorzásával kaphatjuk meg.
Ha a rendszerben holtidő is van, az első előrebecsült időpont a diszkrét holtidő értéke +1.
Az egyenlet jobb oldalának első tagja az ún. szabad választ, a második tagja pedig a gerjesztett választ adja meg. A szabad válasz a múltbeli beavatkozások hatását jelenti a jövőbeni időtartományra, ezen nem tudunk változtatni, ezt a hatást el kell viselni. A gerjesztett válasz az aktuális és a következő beavatkozások hatását adja meg a kimenőjelre. Ezeket a beavatkozásokat megválaszthatjuk úgy, hogy a kimenőjel minél jobban kövessen egy megadott alapjelet egy megadott jövőbeni időtartományban. Csak az aktuális és a jövőbeni időpontokban kifejtett bemenő hatásokkal tudjuk befolyásolni a rendszer jövőbeni viselkedését.
A folyamat modelljét először a folyamat működésének megértésével, a működés matematikai leírásával kaphatjuk meg. Ezt nevezzük fizikai modellezésnek. Ez a modell rendszerint nemlineáris, de általában egy adott munkapont körül linearizálható. A lineáris modellek könnyebben vizsgálhatók, mint a nemlineáris modellek. Lineáris rendszerek leírására, lineáris rendszerekhez szabályozó tervezésére jól alkalmazható általános módszerek állnak rendelkezésre. A lineáris modell struktúráját jelenti a rendszert leíró differenciaegyenlet fokszáma (a kimenőjel aktuális mintavételi értékének megadásához hány előző mintát kell figyelembe venni), és mekkora a diszkrét holtidő értéke (folytonos rendszernél a tárolók, az integrátorok száma, a holtidő értéke). Az adott struktúrán belül meg kell határozni a paraméterek értékeit. Matematikai modellezésről van szó, ha a paramétereket a folyamat bemenetén és kimenetén mért adatok kiértékelésével, az ún. identifikációval határozzuk meg. Feltételezünk egy struktúrát, amelyet általában a fizikai modellezés alapján veszünk fel. Majd a folyamat bemenetét alkalmasan megválasztott jellel gerjesztve mérjük a folyamat kimenőjeleit a mintavételi pontokban. Ha a folyamat üzem közben nem zavarható meg járulékos vizsgálójelekkel, az üzemeltetés közben mérhető bemenőjeleket használjuk fel az identifikációhoz. A folyamat kimenete általában zajjal terhelt, a zajok hatását zajmodellekkel vehetjük figyelembe. Az identifikáció során a modell paramétereit úgy határozzuk meg, hogy a rendszer és a modell kimenőjelei minél jobban illeszkedjenek egymáshoz. Az identifikációra alkalmazhatjuk a legkisebb négyzetek (LS – least squares) módszerét. Ha az identifikációt az adatok összegyűjtése után végezzük el, off-line identifikációról beszélünk. Ha működés közben, a paraméterek feltételezett kezdeti értékéből kiindulva minden egyes mintavételi lépésben a mért bemenő- és kimenőjel értékeket felhasználva módosítjuk a becsült paraméterek értékét, on-line vagy rekurzív identifikációról beszélünk.
Adjuk meg a rendszert impulzusátviteli függvényével:
$G\left(z\right)={Y\left(z\right)\over U\left(z\right)} ={B\left(z^{-1} \right)\over A\left(z^{-1} \right)} {\kern 1pt} {\kern 1pt} {\kern 1pt} z^{-d} $
Az impulzusátviteli függvény racionális törtfüggvény, ahol d a diszkrét holtidő, B és A pedig a $z^{-1} $ hátrafelé toló shift operátor polinomjai:
$A(z^{-1} )=1+a_{1} z^{-1} +...+a_{m} z^{-m} $
$B(z^{-1} )=b_{1} z^{-1} +...+b_{m} z^{-m} $
m a rendszer fokszámát adja meg. m és d adják meg a rendszer struktúráját.
Az impulzusátviteli függvény alapján a rendszer differenciaegyenlete:
$y(t)+a_{1} y(t-1)+...+a_{m} y(t-m)=b_{1} u(t-d-1)+...+b_{m} u(t-d-m)$
Itt most t jelöli a diszkrét időt.
A legkisebb négyzetek módszere
Vezessük be a mért értékeket tartalmazó ún. x megfigyelési vektort és a p paraméter vektort:
$x^{T} =\left[-y\left(t-1\right),...,-y\left(t-m\right),{\kern 1pt} {\kern 1pt} u\left(t-d-1\right),...,{\kern 1pt} {\kern 1pt} u\left(t-d-m\right)\right]$
$p^{T} =\left[a_{1} ,...,a_{m} ,b_{1} ,...,b_{m} \right]$
A kimenőjel felírható a két vektor skalárszorzataként:
$y(t)=x^{T} (t){\kern 1pt} {\kern 1pt} p$
Az off-line legkisebb négyzetek módszerének alkalmazásakor a rendelkezésre álló t =1,…,N mintából keressük a p paramétervektor értékét oly módon, hogy a modell kimenetek és a tényleges mért kimenetek közötti eltérések négyzetének J összege minimális legyen:
$J=\mathop{\sum }\limits_{t=m+d+1}^{N} \left[y(t)-x^{T} p\right]^{{\rm \; 2}} \to \mathop{\min }\limits_{p} $
A J költségfüggvény felírható a következő alakban is:
$J=(Y-Xp)^{T} (Y-Xp)\to \mathop{\min }\limits_{p} $
ahol $Y=\left[\matrix{{y\left(m+d+1\right)} \cr {.} \cr {.} \cr {.} \cr {y\left(N\right)}}\right]$
és $X=\left[\matrix{{x^{T} \left(m+d+1\right)} \cr {x^{T} (m+d+2} \cr {.} \cr {.} \cr {x^{T} \left(N\right)}}\right]=\left[\matrix{{-y{\rm (}m+d{\rm )\; \; \; \; \; ,\; ...,\; }-y{\rm (}d+{\rm 1),\; }u{\rm (}m{\rm )\; \; \; \; \; \; \; ,...,\; \; \; \; \; \; }u{\rm (1)}} \cr {-y{\rm (}m+d+{\rm 1),...,}-y{\rm (}d+{\rm 2),\; }u{\rm (}m+{\rm 1)\; \; ,...,\; \; \; \; \; \; }u{\rm (2)}} \cr {{\rm .}} \cr {{\rm .}} \cr {-y{\rm (}N-{\rm 1)\; \; \; \; \; ,...,\; }-y{\rm (}N-m{\rm ),}u{\rm (}N-d-{\rm 1),...,}u{\rm (}N-d-m{\rm )}}}\right]$
tartalmazzák a mért értékeket.
A J veszteségfüggvényt p szerint differenciálva és a differenciálhányadost zérussá téve megkapjuk az LS módszer számítási összefüggését:
${\partial J\over dp} =-2X^{T} Y+2X^{T} X{\kern 1pt} p=0$
ahonnan
$p=\left[X^{T} X\right]^{-1} X^{T} Y$
Ha a dinamikus rendszernél a kimenetre zaj szuperponálódik, a becslés torzított lesz. Legyen v(t) egy zajsorozat, amely a kimenethez hozzáadódik:
$A\left(z^{-1} \right)y(t)=B\left(z^{-1} \right){\rm \; }u\left(t-d\right)+C\left(z^{-1} \right)v(t)$
Ha $C\left(z^{-1} \right)=1$, ARX modellről, ha $C\left(z^{-1} \right)$ polinom, ARMAX modellről beszélünk. A zajmodell befolyásolja a zajos mérésekből történő identifikáció jóságát.
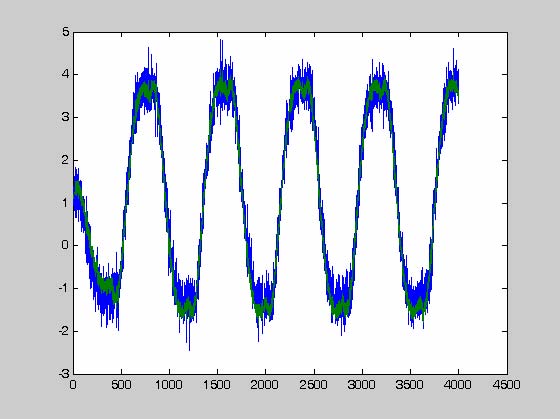
15. ábra Zajos folyamat kimenőjele
Szemléltető példaként egy ismeretlen zajos rendszer négyszögjelsorozatra adott válaszát mutatja a 15. ábra (kék görbe). A bemenőjeleket és a kimenőjeleket 0.5 sec mintavételi időközönként vettük fel és tároltuk.
m=2 és d=1 felvételével, és C fokszámát ugyancsak 2-re felvéve az identifikált paraméterek:
$A\left(z^{-1} \right)=1-1.99z^{-1} +0.9904z^{-1} $
$B\left(z^{-1} \right)=-0.0052z^{-1} +0.005313z^{-2} $
$C\left(z^{-1} \right)=1-1.935z^{-1} +0.9352z^{-2} $
Az identifikált folyamat kimenőjele (zöld görbe a 15. ábrán) jól illeszkedik a mért görbéhez.
(Az LS algoritmus kiértékeléséhez a MATLAB program identifikációs toolboxának utasításait használtuk.)
Jelöljük az N számú megfigyelés alapján számított paramétervektort $\Theta _{N}^{T} $-nel.
$\Theta _{N}^{T} =p^{T} =\left[a_{1} ,...,a_{m} ,b_{1} ,...,b_{m} \right]$
Az off-line identifikációval számított paramétervektor az alábbi alakban adható meg:
$\theta _{N} =\left[X_{N}^{T} X_{N} \right]^{-1} X_{N}^{T} Y_{N} $
A legkisebb négyzetek módszerének rekurzív számításánál feltételezzük, hogy rendelkezésre áll a paraméterek N mintán alapuló LS becslése, és egy új N+1-edik megfigyelés felhasználásával kívánjuk frissíteni a paraméterek becslését. Nem rekurzív megoldás esetén ez a becslés
$\theta _{N+1} =\left[X_{N+1}^{T} X_{N+1} \right]^{-1} X_{N+1}^{T} Y_{N+1} $
alapján állítható elő. Megállapíthatjuk, hogy az X és Y mátrix ill. vektor növekvő dimenziójú. A dimenzió növekedése és a lépésenkénti mátrix inverzió elkerülhető. Néhány átalakítási lépés után $\theta _{N+1} $ meghatározható $\theta _{N} $ ismeretében az alábbi összefüggések segítségével:
$\theta _{N+1} =\theta _{N} +{P_{N} x_{N+1} \over 1+x_{N+1}^{T} P_{N} x_{N+1} } \left(y_{N+1} -x_{N+1}^{T} \theta _{N} \right)$
ahol
$P_{N+1} =P_{N} -{P_{N} x_{N+1} x_{N+1}^{T} P_{N} \over 1+x_{N+1}^{T} P_{N} x_{N+1} } $
az ún. konvergenciamátrix. A fenti összefüggésekben $y_{N+1} $ az $Y_{N+1} $ vektor utolsó eleme, $x_{N+1}^{T} $ pedig az $X_{N+1} $ mátrix utolsó sora. A rekurzív (RLS) megoldás matematikailag megegyezik a nem rekurzív LS becsléssel, ugyanakkor számítástechnikailag kedvezőbb. Nem igényel minden lépésben mátrix inverziót, ugyanakkor a rekurzív eljárás indításához rendelkezésre kell hogy álljanak a $\theta _{0} $ és $P_{0} $ induló értékek. Ezek az értékek előzetes ismeretek alapján képezhetők.
A rekurzív legkisebb négyzetek módszerének összefüggései időben változó paraméterek követését nem teszik lehetővé, mivel a régen megszerzett információt is ugyanolyan súllyal veszik figyelembe, mint az aktuális megfigyelést. A paraméterek időbeli változásának követése érdekében a régen szerzett információt fokozatosan el kell felejteni. A régebbi megfigyeléseket a becslésnél kisebb súllyal kell figyelembe venni. Az idővariáns paraméterkövetésnek az egyik lehetséges módja a J költségfüggvényben a megfigyelések exponenciális súlyozása egy $\alpha$ felejtési tényezővel (0$<$$\alpha$$<$$=$1). A felejtési tényezővel a becslési összefüggések az alábbiak szerint módosulnak:
$\theta _{N+1} =\theta _{N} +{P_{N} x_{N+1} \over \alpha +x_{N+1}^{T} P_{N} x_{N+1} } \left(y_{N+1} -x_{N+1}^{T} \theta _{N} \right)$
és
$P_{N+1} ={1\over \alpha } \left(P_{N} -{P_{N} x_{N+1} x_{N+1}^{T} P_{N} \over \alpha +x_{N+1}^{T} P_{N} x_{N+1} } \right)$
A felejtési tényező megválasztását a megkívánt paraméterkövetési sebesség, a folyamatot érő zajhatás és a folyamat gerjesztésének figyelembevételével lehet meghatározni.
Összefoglalva: Ha a paramétereket nem ismerjük, de időközben nem változnak, jó becslést kapunk, ha a felejtési tényezőt 1-re választjuk. Ha azonban a paraméterek változnak, bizonyos mértékig felejteni kell a régebbi információkat, hogy meg tudjuk tanulni az új, megváltozott értékeket.
A rekurzív tanulás jellegét az alábbi példán szemléltetjük.
A 16. ábra mutatja a másodrendű folytonos rendszert és mintavételezett modelljét, amely impulzusátviteli függvényével adott. A simulink programban a rendszert és modelljét egy jelgenerátor által szolgáltatott véletlenszerű négyszögimpulzus sorozattal gerjesztjük (sárga görbe a 17. ábrán). A bemenőjelet és a kimenőjelet mérjük, és minden időpillanatban az RLS becslővel megbecsüljük az impulzusátviteli függvény paramétereit, amelyeket a diszkrét modellben beállítunk.
A change blokkok beállítható (itt 250 sec) időpillanatban megváltoztatják a folytonos szakasz paramétereit, a „partank” blokk minden időpillanatban beállítja a modellben az identifikált paraméterértékeket.
A 17. ábra mutatja a szimulációs eredményeket $\alpha =1$ mellett. A sárga görbe a bemenőjel (gerjesztés), a kék görbe a folytonos rendszer kimenőjele, a lila görbe a modell kimenete.
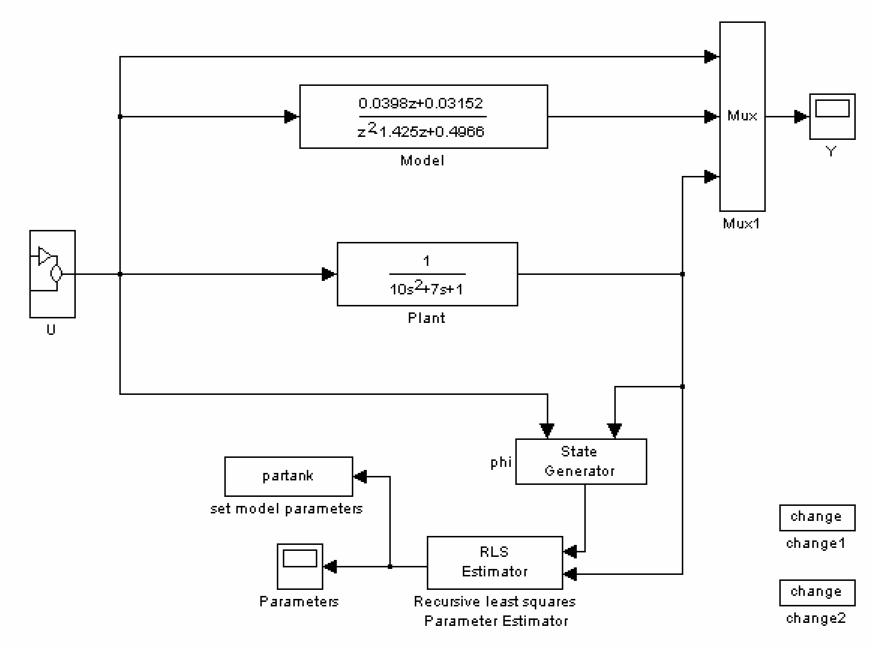
16. ábra Másodrendű rendszer rekurzív (on-line) identifikációja
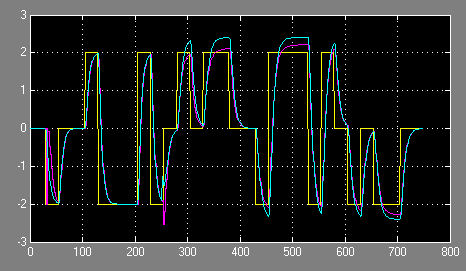
17. ábra A rendszer és az identifikált modell kimenőjelei $\alpha =1$ mellett
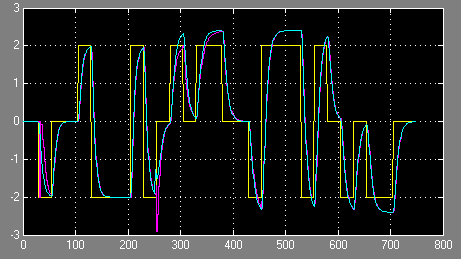
18. ábra A rendszer és az identifikált modell kimenőjelei $\alpha =0.98$ mellett
Látható, hogy 250 sec-ig az algoritmus megtanulta a paraméterek értékeit, és a folyamat és modelljének kimenőjelei közel azonosak, a rendszer és modelljének kimenőjelei egybeesnek. A paraméterváltozás után azonban a modell kimenőjele állandósult állapotban nem áll be a rendszer kimenőjelének értékére, az identifikáció nem adja meg pontosan a paraméterek megváltozott értékeit. Ha azonban az $\alpha =0.98$ felejtési tényezővel megengedjük a korábbi mért értékek súlyozását (felejtését), az eljárás megtanulja az új paraméterértékeket és a rendszer kék és a modell lila kimenőjelei a paraméterváltozás után is egybeesnek (18. ábra). A 19. ábra szemlélteti a paraméterek változását a tanulás során. Megjegyezzük, hogy az impulzusátviteli függvényben a paramétereket legalább négy tizedesjegy pontossággal kell megadni.
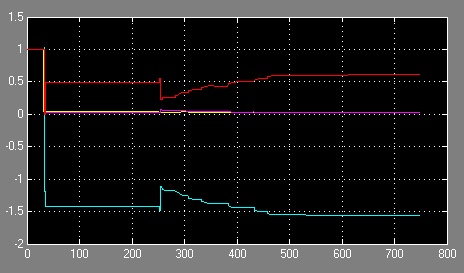
19. ábra A paraméterek beállása a rekurzív identifikáció során
Keviczky et al. (2009, 2011)
Ljung (1999)