

Folytonos folyamatok állapotteres leírása
A bemeneti-kimeneti modellek az y kimenőjel és az u bemenőjel között írják le a kapcsolatot, amely rendszerint egy n-edrendű differenciálegyenlettel adható meg.
A rendszernek vannak belső változói, ún. állapotváltozói is. Az állapotváltozókra jellemző, hogy pillanatnyi értéküket a rendszerben a múltban bekövetkezett változások alakították ki, és a bemenőjel hirtelen változására nem képesek hirtelen változásokkal válaszolni, a bemenőjel által meghatározott új értéküket fokozatosan érik el.
Az állapotegyenlet megadja az összefüggést a bemenőjel, az állapotváltozók és a kimenőjel között. Tekintsünk egy egy-bemenetű, egy-kimenetű (SISO - Single Input - Single Output) rendszert. Az $x_{1} ,x_{2} ,...,x_{n} $ állapotváltozók alkotják az x állapotvektor komponenseit. A rendszer u bemenőjele, x állapotváltozói és y kimenőjele között az alábbi nemlineáris állapotegyenlet adja meg az összefüggést:
$\frac{dx\left(t\right)}{dt} =\dot{x}\left(t\right)=f\left[x\left(t\right),u\left(t\right)\right]$
$y\left(t\right)=g\left[x\left(t\right),u\left(t\right)\right] $
f és g nemlineáris függvények.
Ha a rendszer lineáris, az állapotegyenlet a következő alakban adható meg:
$\frac{dx\left(t\right)}{dt} =Ax\left(t\right)+bu\left(t\right)$
$y\left(t\right)=c^{T} x\left(t\right)+du\left(t\right)$
ahol az $\left\{A,b,c^{{\rm T}} ,d\right\}$mátrixok a rendszert jellemző paramétermátrixok.
Az állapotegyenlettel megadott rendszer blokkvázlatát az 1. ábra mutatja.
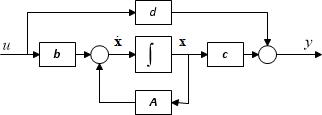
1. ábra Lineáris időinvariáns rendszer állapotdiagramja
Az állapotváltozók tulajdonságaival azok lineáris kombinációi is rendelkeznek. Az állapotegyenletek tehát igen sokféleképpen adhatók meg, miközben a kimenőjel és a bemenőjel közötti átvitel ugyanaz. Ezek az alakok egymásba áttranszformálhatók. Egyes reprezentációkban az állapotváltozóknak fizikai jelentése van. Más reprezentációkban a számítások, pl. az állapotegyenlet megoldása egyszerűbb.
Az állapotegyenlet megoldása
Az időtartományban az állapotegyenlet megoldása:
$x(t)=e^{A\, t} x(0)+\int _{0}^{t}e^{A\, (t-\tau )} b\, u(\tau )d\tau $
Analitikusan akkor számítható ki zárt alakban, ha az A mátrix diagonális (kanonikus alak). Ekkor egyszerű bemenőjelekre, például egységugrásra a gerjesztett válasz is könnyen számítható. Célszerű tehát az állapotegyenletet és a kezdeti feltételeket is kanonikus alakra transzformálni, a kanonikus egyenletet megoldani az adott kezdeti feltételekre és a megadott gerjesztésre, majd a megoldást visszatranszformálni az állapotváltozók eredeti koordinátarendszerére.
A Laplace operátortartományban az állapotegyenlet megoldása:
Az operátortartományban az állapotváltozók Laplace transzformáltja az alábbi összefüggéssel számítható:
$x(s)=(sI-A)^{-1} x(0)+(sI-A)^{-1} bU(s)$
A kimenőjel pedig
$Y(s)=[c(sI-A)^{-1} b+d]U(s)$
Az átviteli mátrix (ami egy bemenet egy kimenet esetén a rendszer átviteli függvénye):
$H(s)=\frac{Y(s)}{U(s)} =c(sI-A)^{-1} b+d$
Állapottranszformációk
Legyenek az új állapotkoordináták felülvonással jelölve. Az új és az eredeti állapotváltozók között a T transzformációs mátrix adja meg az összefüggést.
$\bar{x}=Tx{\rm} $ és $x=T^{-1} \bar{x}$
Az új, felülvonással jelölt állapotkoordinátákban az állapotegyenletek:
$\dot{\bar{x}}=\bar{A}\bar{x}+\bar{b}u$
$y=\bar{c}\bar{x}+\bar{d}u$
Az új paramétermátrixok az eredeti paramétermátrixokból az alábbi összefüggésekkel kaphatók meg:
${\bar{A}=TAT^{-1} ,\, {\rm \; }\, \bar{b}=Tb,\, {\rm \; }\, \bar{c}=cT^{-1} ,\, \, \, \bar{d}=d} $
Ezek az ún. hasonlósági transzformáció összefüggései.
Ha a $T^{-1}$ mátrix oszlopvektorai az A mátrix sajátvektorai, az $\bar{A}$ mátrix diagonális lesz. Ezt az állapotreprezentációt kanonikus alaknak nevezzük.
A kanonikus alakban az állapotegyenlet megoldása egyszerűbb, mint az eredeti állapotváltozós alakban, különösen, ha a gerjesztés egyszerű jel, például egységugrás.
Irányíthatóság, megfigyelhetőség
R. Kalman bevezette az irányíthatóság és a megfigyelhetőség fogalmát.
Egy rendszer akkor állapotirányítható, ha az állapotváltozók a bemenőjellel egymástól függetlenül elvihetők kezdeti értékeikből egy végső időpontra megadott végső értékükbe. Egy rendszer akkor kimeneti irányítható, ha kimenőjele a bemenőjellel elvihető kezdeti értékéről a végső időpontban megadott értékére.
Egy rendszer akkor megfigyelhető, ha a kimenőjel regisztrátumából vissza lehet következtetni az állapotváltozók kezdeti értékeire egymástól függetlenül.
Ezeket a tulajdonságokat az állapotegyenlet kanonikus alakjából könnyen meg lehet adni. Az A mátrix átlójában szereplő elemeknek kölönbözőknek kell lenniük. Ha a kanonikus alakban a b oszlopvektornak van zérus eleme, akkor az ahhoz tartozó állapotváltozó nem irányítható. Ha a rendszer valamelyik állapotváltozója nem irányítható, még kimeneti irányítható lehet, ha a kimenőjelet a bemenőjel egy másik, irányítható állapotváltozón keresztül befolyásolja. Ha a c sorvektornak van zérus eleme, akkor az annak megfelelő állapotváltozó nem megfigyelhető.
Az irányíthatóság és megfigyelhetőség tulajdonsága megállapítható a rendszer általános állapotreprezentációjából is a Kalman-féle irányíthatósági és megfigyelhetőségi feltételek vizsgálatával [see Keviczky et al.].
Példa az irányíthatóság és megfigyelhetőség meghatározására
Legyen egy rendszer állapotegyenlete:
$ \left[\begin{array}{c} {\dot{x}_{1} } \\ {\dot{x}_{2} } \\ {\dot{x}_{3} } \end{array}\right]= $$\left[\begin{array}{ccc} {-1} & {-0.5} & {0.5} \\ {2} & {-3} & {0} \\ {2} & {-1} & {-2} \end{array}\right]\cdot \left[\begin{array}{c} {x_{1} } \\ {x_{2} } \\ {x_{3} } \end{array}\right] $$+\left[\begin{array}{c} {2} \\ {3} \\ {1} \end{array}\right]\cdot u $
${y=\left[\begin{array}{ccc} {0} & {0} & {1} \end{array}\right]\cdot \left[\begin{array}{c} {x_{1} } \\ {x_{2} } \\ {x_{3} } \end{array}\right]+0\cdot u} $
Vizsgáljuk meg, hogy a rendszer állapotirányítható, kimeneti irányítható és megfigyelhető-e?
Transzformáljuk az állapotegyenletet kanonikus alakra.
Ehhez meg kell határozni az A mátrix sajátvektorait és azokat el kell helyezni a T transzformációs mátrix inverzének oszlopaiba. Majd a hasonlósági transzformáció összefüggéseivel határozzuk meg a kanonikus koordinátákban az állapotegyenletet.
A kanonikus állapotegyenlet a következő:
$\left[\begin{array}{c} {\dot{\bar{x}}_{1} } \\ {\dot{\bar{x}}_{2} } \\ {\dot{\bar{x}}_{3} } \end{array}\right]=$ $\left[\begin{array}{ccc} {-1} & {0} & {0} \\ {0} & {-3} & {0} \\ {0} & {0} & {-2} \end{array}\right]\cdot \left[\begin{array}{c} {\bar{x}_{1} } \\ {\bar{x}_{2} } \\ {\bar{x}_{3} } \end{array}\right]$ $+\left[\begin{array}{c} {1.73} \\ {0} \\ {-2.23} \end{array}\right]\cdot u $
$ {y=\left[\begin{array}{ccc} {0.57} & {-0.707} & {0} \end{array}\right]\cdot \left[\begin{array}{c} {\bar{x}_{1} } \\ {\bar{x}_{2} } \\ {\bar{x}_{3} } \end{array}\right]+0\cdot u}$
A kanonikus állapotegyenlet alapján felrajzolhatjuk a rendszer blokkvázlatát (2. ábra).
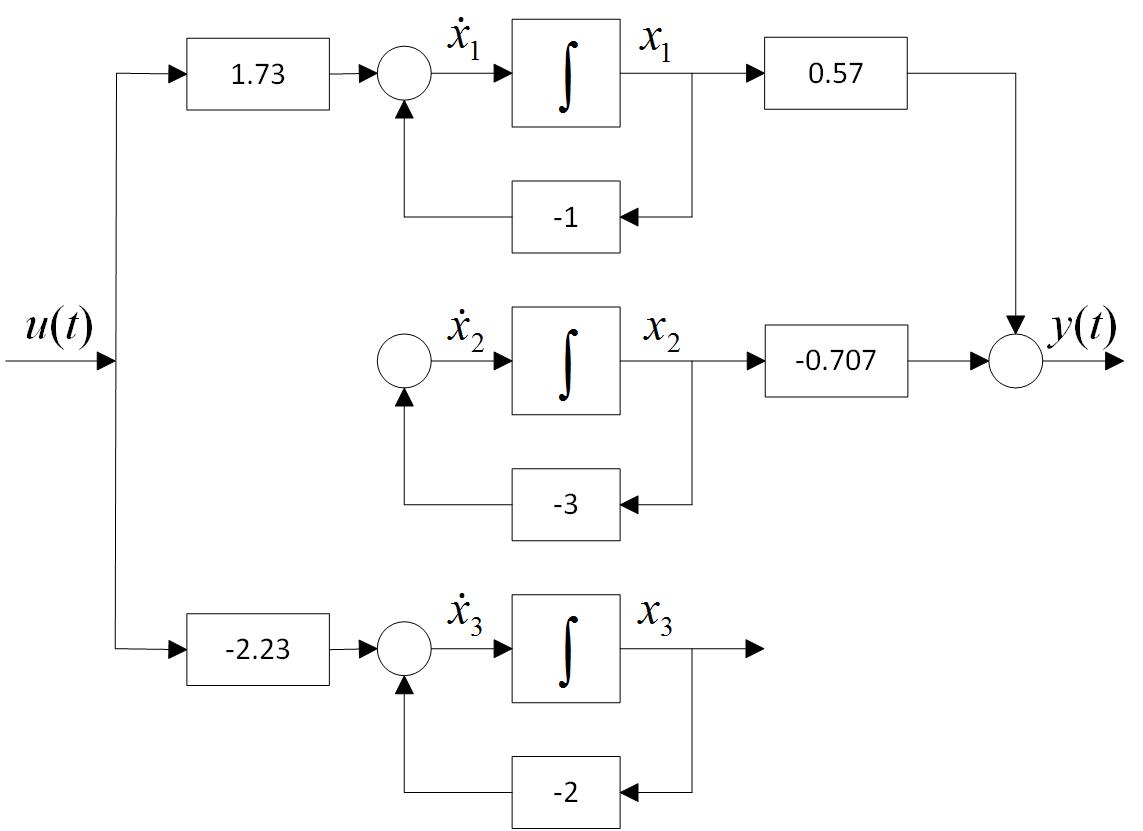
2. ábra Az állapotegyenlet kanonikus alakjának blokkvázlata
Az állapotegyenletből és blokkvázlatából is látható, hogy a rendszer nem állapotirányítható, mivel a második állapotváltozó nem befolyásolható a bemenőjellel. A rendszer kimeneti irányítható, mivel a bemenőjel az első állapotváltozón keresztül befolyásolja a kimenőjelet. A rendszer nem megfigyelhető, mivel a kimenőjel nem tartalmaz információt a harmadik állapotváltozóról.
A kimenőjel és a bemenőjel kapcsolatát csupán a rendszer irányítható és megfigyelhető állapotváltozói határozzák meg, példánkban csupán az első állapotváltozó befolyásolja a kimenőjelet.
A másik két állapotváltozó változása is befolyásolja azonban a rendszer állapotát, amit célszerű figyelembe venni. Például egy motor fordulatszámát változtatjuk a ráadott kapocsfeszültséggel. A motor fordulatszáma a kimenőjel, de ugyanakkor állapotváltozó is. A kapocsfeszültség befolyásolja a motor hőmérsékletét, ami szintén állapotváltozó. A hőmérséklet nem befolyásolja a fordulatszámot, de figyelni kell, a motor tervezésekor a hőviszonyokat is figyelembe kell venni, hogy működés közben a motor ne melegedjen túl, ne égjen le.
Egy rendszer állapotváltozós leírása több információt tartalmaz a rendszerről, mint az átviteli függvény, ha a rendszerben vannak nem irányítható vagy nem megfigyelhető állapotváltozók.
Ha egy szabályozási körben a szabályozó zérusaival „kiejtjük” a folyamat kedvezőtlen pólusait, akkor az eredő rendszer vagy nem irányíthatóvá, vagy nem megfigyelhetővé válik, miközben a kimenet irányítható. (A „kiejtett” pólus ott van a rendszerben, csak a bemenet – kimenet vonatkozásában válik rejtetté.)
Hivatkozások:
Keviczky et al. (2009, 2011)
Hetthéssy et al. (2014)