
Leírás az időtartományban, a frekvenciatartományban és az operátortartományban
Egy-bemenetű egy-kimenetű (SISO – Single Input Single Output) folytonos dinamikus rendszert feltételezünk. A rendszer kimenőjelének időbeli alakulását kívánjuk meghatározni a rendszert gerjesztő bemenet hatására. A jel adott időpontbeli megváltozása (deriváltja) alakítja a jelet. (Például szabadesésnél a gyorsulás alakítja a test sebességét az időben, a sebesség pedig az elmozdulást.)
A legkülönbözőbb folyamatok általában matematikailag azonos alakú differenciálegyenletekkel (vagy differenciálegyenlet-rendszerekkel) írhatók le, amelyek a változók és azok megváltozásainak kapcsolatát adják meg. Mechanikai mozgások, villamos és mágneses jelenségek, hőfolyamatok, gázok és folyadékok áramlása, stb. differenciálegyenletekkel írhatók le. A differenciálegyenleteket a fizikai rendszer működését analizálva adhatjuk meg.
Egy folytonos, lineáris egy-bemenetű egy-kimenetű (SISO, Single Input Single Output) időinvariáns rendszer az időtartományban leírható egy n-edrendű differenciálegyenlettel vagy n darab elsőrendű differenciálegyenlet rendszerével (ún. állapotegyenlettel), illetve jellemezhető tipikus gerjesztésekre adott válaszaival.
Az n-edrendű differenciálegyenlet alakja:
$a_{n} \frac{d^{n} y\left(t\right)}{dt^{n} } +a_{n-1} \frac{d^{n-1} y\left(t\right)}{dt^{n-1} } +...+a_{1} \frac{dy\left(t\right)}{dt} +a_{0} y\left(t\right)=$$b_{m} \frac{d^{m} u\left(t\right)}{dt^{m} } +b_{m-1} \frac{d^{m-1} u\left(t\right)}{dt^{m-1} } +...+b_{1} \frac{du\left(t\right)}{dt} +b_{0} u\left(t\right)$
u a bemenőjelet, y a kimenőjelet jelöli. $a_{0} ,a_{1} , a_{2} ,...,a_{n} ,\, b_{0} , b_{1} ,...,b_{m} $ a rendszer paraméterei, amelyek ismertek, vagy mérések alapján határozhatók meg.
Az egyenlet jobb oldala a g(t) gerjesztés:
$g\left(t\right)=b_{m} \frac{d^{m} u\left(t\right)}{dt^{m} } +b_{m-1} \frac{d^{m-1} u\left(t\right)}{dt^{m-1} } +...+b_{1} \frac{du\left(t\right)}{dt} +b_{0} u\left(t\right)$
Ha a kimenőjel csak késleltetve, ún. holtidős eltolással válaszol a bemenőjel változásaira, a differenciálegyenlet jobb oldalán a változók argumentuma $t-T_{d} $ , ahol $T_{d} $ a holtidő. A differenciálegyenlet ekkor a következő alakú:
$\ {a_{n} \frac{d^{n} y\left(t\right)}{dt^{n} } +a_{n-1} \frac{d^{n-1} y\left(t\right)}{dt^{n-1} } +...+a_{1} \frac{dy\left(t\right)}{dt} +a_{0} y\left(t\right)=} $
$\ {\quad b_{m} \frac{d^{m} u\left(t-T_{d} \right)}{dt^{m} } +b_{m-1} \frac{d^{m-1} u\left(t-T_{d} \right)}{dt^{m-1} } +...+b_{1} \frac{du\left(t-T_{d} \right)}{dt} +b_{0} u\left(t-T_{d} \right)} $
A holtidő pl. szállítási folyamatoknál jelentkezik, amikor a bemenőjel változásának hatása egy távolabbi érzékelési ponton késleltetve mérhető.
A fizikai realizálhatóság feltétele: $m\le n$ .
Csak ennek fennállása esetén marad a kimenőjel véges a bemenőjel véges megváltozása esetén.
A differenciálegyenlet elvileg végtelen sok megoldása közül azt kell kiválasztani, amely eleget tesz az y függvényre vonatkozó peremfeltételeknek. y(t) -re és differenciálhányadosaira n db olyan feltételt kell előírni, amelyeket a megoldásnak ki kell elégítenie. A peremfeltételek rendszerint kezdeti feltételek, tehát a kimenőjel és annak deriváltjainak t=0 időpontbeli értékeit adjuk meg.
A differenciálegyenletet sokszor az alábbi ún. időállandós alakban írjuk fel:
$ {T_{n}^{n} \frac{d^{n} y\left(t\right)}{dt^{n} } +T_{n-1}^{n-1} \frac{d^{n-1} y\left(t\right)}{dt^{n-1} } +...+T_{1} \frac{dy\left(t\right)}{dt} +y\left(t\right)=} $
$A($$\tau _{m}^{m} \frac{d^{m} u\left(t-T_{d} \right)}{dt^{m} } +\tau _{m-1}^{m-1} \frac{d^{m-1} u\left(t-T_{d} \right)}{dt^{m-1} } +...+\tau _{1} $$\frac{du\left(t-T_{d} \right)}{dt} +u\left(t-T_{d} \right))$
ahol $A=\frac{b_{0} }{a_{0} } $ a rendszer átviteli tényezője, amely megadja a kimenőjel és a bemenőjel viszonyát állandósult állapotban. Az átviteli tényező nemcsak puszta szám, hanem fizikai dimenziója is lehet.
$T_{i} =\sqrt[{i}]{a_{i} /a_{0} } $ és $\tau _{j} =\sqrt[{j}]{b_{j} /b_{0} } $ időállandók, dimenziójuk sec.
Az időállandós alak előnye, hogy a differenciálegyenlet tényleges megoldása nélkül is, a paraméterek alapján következtetni lehet tipikus bemenőjelekre adott válaszok időbeli alakulására.
Az átviteli tényező fenti értelmezése természetesen csak akkor érvényes, ha és zérustól különböző számok. Ha pl. $a_{0} =0$, az átviteli tényező $A=b_{0} /a_{1} $ , és ekkor az időállandók értelmezése is megváltozik.
A differenciálegyenlet a teljes vagy inhomogén differenciálegyenlet, amely g(t)=0 esetén homogén egyenletté válik.
A rendszer működését differenciálegyenletének megoldása írja le. A megoldás két komponensből áll, a homogén egyenlet $y_{h} \left(t\right)$ általános megoldásából és az inhomogén egyenlet egy $y_{i} \left(t\right)$ partikuláris megoldásából.
$y\left(t\right)=y_{h} \left(t\right)+y_{i} \left(t\right)$
A homogén egyenlet megoldását a karakterisztikus egyenlet gyökei alapján határozhatjuk meg. A karakterisztikus egyenletet úgy kapjuk meg, hogy a homogén egyenletbe y deriváltjai helyébe egy s változó megfelelő hatványait helyettesítjük. A karakterisztikus egyenlet tehát:
$a_{n} s^{n} +a_{n-1} s^{n-1} +...+a_{1} s+a_{0} =0$
Egyszeres gyökök esetén a homogén egyenlet általános megoldása a következő alakú:
$y_{h} \left(t\right)=k_{1} e^{s_{1} t} +k_{2} e^{s_{2} t} +...+k_{n} e^{s_{n} t} $
ahol $s_{1} ,s_{2} ,...,s_{n} $ a rendszer karakterisztikus egyenletének a gyökei. A $k_{i} $ konstansokat a kezdeti értékekből kell meghatározni. (Többszörös gyökök esetén a megoldás alakja módosul, erre most nem térünk ki.)
Az inhomogén egyenlet egy partikuláris megoldását, amely az u bemenőjeltől függ, jelöljük f(u)-val. Feltételezve, hogy valamilyen eljárással – pl. kísérletező feltevéssel vagy az állandók variálásának módszerével, esetleg egyszerű megfontolással – sikerült megtalálni. A differenciálegyenlet általános megoldása:
$y\left(t\right)=y_{h} \left(t\right)+f\left(u\right)=k_{1} e^{s_{1} t} +...+k_{n} e^{s_{n} t} +f\left(u\right)$
A $k_{i} $ konstansokat a kezdeti feltételek ismeretében kell meghatározni.
A differenciálegyenlet megoldása az időtartományban sokszor bonyolult és fáradságos. A karakterisztikus egyenletnek csak negyedfokú esetig van analitikus megoldása. Magasabbfokú esetben numerikus eljárásokat alkalmazhatunk a gyökök meghatározására. Az inhomogén egyenlet egy partikuláris megoldásának megtalálása bonyolultabb bemenőjel esetén számításigényes.
Egyszerű gerjesztésekre a megoldás könnyebben határozható meg.
Ugrásalakú gerjesztésre a differenciálegyenlet alakjából a megoldás kezdeti és végértékeire néhány megállapítást tehetünk. Tekintsük a differenciálegyenlet együtthatókkal megadott alakját. Legyen a bemenőjel egységugrás, $g\left(t\right)=b_{0} 1\left(t\right)$. A t=0 időpontban csak a legmagasabbrendű derivált értéke ugorhat. (Ugyanis a differenciálegyenlet két oldalának minden időpontban egyensúlyban kell lennie, és ha pl. a kimenőjel alacsonyabbrendű deriváltjában is ugrás lenne, az impulzusszerű változást eredményezne a magasabbrendű deriváltakban.)
$a_{n} \left. \frac{d^{n} y\left(t\right)}{dt^{n} } \right|_{t=0} =b_{0} $
tehát
$\left. \frac{d^{n} y\left(t\right)}{dt^{n} } \right|_{t=0} =b_{0} /a_{n} $
(Mechanikai mozgást tekintve például a tömegre ható erő megváltozásakor először csak a gyorsulás értéke változik meg, majd idővel ez létrehozza a sebesség és az elmozdulás megváltozását is.)
Ha a tranziensek lecsengenek, a kimenőjel valamennyi deriváltja zérus értékű lesz, és a kimenőjel az átviteli tényező értékén állandósul: $y\left(t\to \infty \right)=b_{0} /a_{0} $
A differenciálegyenlet megoldása felbontható kvázistacionárius és tranziens összetevőkre. A bemenőjel hatására állandósult állapotban fennmaradó kimenőjel a kvázistacionárius megoldás. A rendszer tehetetlensége miatt a kimenőjelben a gerjesztő bemenőjel hirtelen változására nem jelenhet meg ugrásszerű változás. Ha a kvázistacionárius megoldás kezdeti értéke zérustól eltér, a létrejövő tranziens komponens ezt kiegyenlíti. A tranziens megoldás a rendszer dinamikájától, a karakterisztikus egyenlet gyökeitől függ.
A tranziens mozgás lefolyása alapvetően tükrözi a rendszer sajátosságait. Ha a tranziens összetevők az időben csillapodnak, a gerjesztésnek megfelelő új egyensúlyi állapot beáll, a rendszer stabilis. Az egyre növekvő tranziens mozgás labilis viselkedést jelent, ilyenkor új egyensúlyi állapot nem érhető el. Csillapítatlan periodikus tranziens mozgás a stabilitás határesete, ami arra is utal, hogy a tranziens lengés frekvenciájával azonos frekvenciájú gerjesztő jelekre a rendszer rezonálni fog. A rendszer stabilitása a karakterisztikus egyenlet gyökei alapján dönthető el.
A Példa ablakban bemutatjuk egy elsőrendű differenciálegyenlet megoldását egységugrás bemenőjelre.
A szabályozási rendszer differenciálegyenletének megoldása megadja tetszőleges bemenőjelre a kimenőjel időbeli lefolyását. Az inhomogén egyenlet egy partikuláris megoldásának meghatározása annál könnyebb, minél egyszerűbb a gerjesztő függvény.
A rendszert olyan tipikus bemenőjellel célszerű gerjeszteni, amely jelentős tranziens mozgást képes előidézni. Ekkor a kimenőjel lefolyása jellemző lesz a rendszer jelátviteli tulajdonságaira, menetéből következtetéseket vonhatunk le a rendszer struktúrájára és paramétereire vonatkozóan.
A legfontosabb vizsgálójelek
- az egységimpulzus függvény (Dirac delta): $\delta (t)$,
- az egységugrás függvény: $1\left(t\right)$ ,
- az egységsebességugrás függvény: $t1\left(t\right)$ ,
- az egységgyorsulásugrás függvény: $\frac{t^{2} }{2} 1\left(t\right)$ .
A tipikus vizsgálójelekre adott válaszok a tipikus rendszerválaszok (1. ábra).
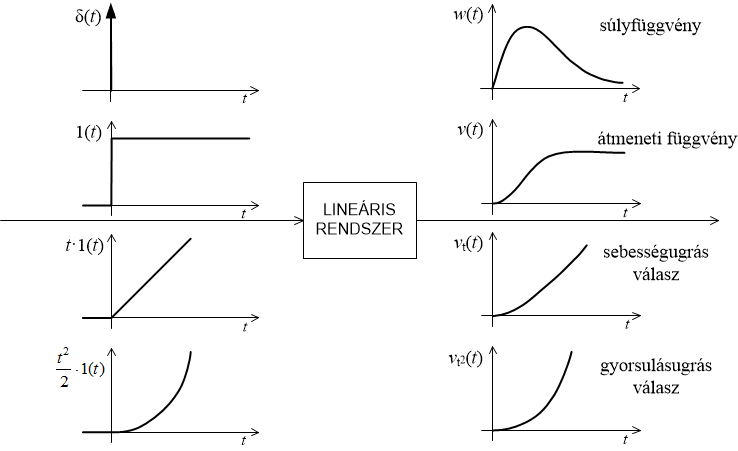
- ábra Tipikus bemenőjelek és válaszok
A súlyfüggvény a rendszer Dirac delta bemenőjelre adott válasza, az átmeneti függvény az egységugrásra adott válasz. A súlyfüggvény és az átmeneti átmeneti függvény rendszerjellemzők, menetükből következtetések vonhatók le a rendszer struktúrájára és paramétereire. Ismeretükben a rendszer tetszőleges bemenőjelre adott válasza is meghatározható.
Az elsőrendű differenciálegyenlet megoldását Dirac delta illetve egységugrás bemenőjelre, vagyis súlyfüggvényének és átmeneti függvényének meghatározását a Példa ablakban mutatjuk meg.
Mivel a differenciálegyenlet megoldása sokszor nehézkes, különböző módszerek alakultak ki a vizsgálatok egyszerűsítésére. A differenciálegyenlet Laplace operátortartományba való transzformálásával a differenciálegyenlet helyett algebrai egyenletet kell megoldani. A frekvenciatartománybeli vizsgálatok az időtartománybeli viselkedés gyors közelítő kiértékelésére adnak lehetőséget.
A rendszerek időbeli viselkedésének meghatározása, kimenőjeleik, belső változóik válaszának megadása a gerjesztések és a kezdeti feltételek hatására fontos a rendszer viselkedésének elemzése, majd a szabályozás tervezése szempontjából.
A rendszerek viselkedését az időtartományban szeretnénk vizsgálni. Sokszor azonban a vizsgálat nem egyszerű. Ha más szemléletmóddal közelítjük meg a problémát, esetleg könnyebben jutunk eredményre. Transzformálhatjuk a feladatot a frekvenciatartományba vagy az operátortartományba, ahol a megoldás egyszerűbb lehet, majd inverz transzformációval visszatérünk az időtartományba, ahol értékelhetjük a rendszer időbeli viselkedését.
Az időtartományban a rendszerek viselkedését általában differenciálegyenletekkel írjuk le, ezek megoldása az adott bemenőjelre a megadott kezdeti feltételekkel sokszor fáradságos. A megoldás egyszerűbb, ha tipikus bemenőjelekkel számolunk, például egységugrással vagy impulzusfüggvénnyel. Ezek a tipikus válaszok, az ún. átmeneti függvény, vagy a súlyfüggvény jellemzők a rendszerre (lásd időtartománybeli vizsgálat).
Lineáris állandó együtthatójú differenciálegyenletek tárgyalásának a műszaki alkalmazások szempontjából előnyös módja az, ha függvénytranszformációkkal az eredeti időfüggvényekről azokkal egyértelmű kapcsolatban álló olyan függvényekre térünk át, amelyekkel az eredeti differenciálegyenlet helyett algebrai egyenletet kell megoldani.
Ilyen eljárások a Fourier és a Laplace-transzformáció.
A transzformáció segítségével a differenciálegyenletet algebrai egyenletté alakítjuk (az egyszerűség kedvéért zérus kezdeti értékeket tételezünk fel), az algebrai egyenletet megoldjuk, majd a kimenőjel transzformáltját visszatranszformálva megkapjuk a számunkra érdekes időfüggvényt.
Ha ismerjük egy lineáris rendszer válaszát a különböző frekvenciájú szinuszos jelekre (a frekvencia nulla és végtelen között változik), akkor elvileg meg tudjuk adni a rendszer válaszát egy periodikus, illetve egy aperiodikus jelre. Ennek magyarázatát, matematikai hátterét a Fourier sorfejtés adja meg.
Egy periodikus y(t) jel felbontható harmonikus (szinuszos és koszinuszos) függvények összegére. Ez az összeg a Fourier sort adja meg, amelynek elemei diszkrét frekvenciákhoz rendelhetők. Legyen a jel periódusideje T, alapkörfrekvenciája pedig $\omega _{0} =2\pi /T$ .
A jel közelítően megadható Fourier sorával:
$y\left(t\right)\sim a_{0} +\sum _{n=1}^{\infty }\left(a_{n} \cos n\omega _{0} t+b_{n} \sin n\omega _{0} t\right)$
ahol
$a_{0} =\frac{1}{T} \int _{-T/2}^{T/2}y(t) dt$
$a_{n} =\frac{2}{T} \int _{-T/2}^{T/2}y\left(t\right)\cos \left(n\omega _{0} t\right) dt$
$b_{n} =\frac{2}{T} \int _{-T/2}^{T/2}y\left(t\right)\sin \left(n\omega _{0} t\right) $
A Fourier sor komplex alakban is megadható:
$y\left(t\right)=\sum _{n=-\infty }^{\infty }c_{n} e^{jn\omega _{0} t}$
ahol n egész szám, és
$c_{n} =\frac{1}{T} \int _{-T/2}^{T/2}y\left(t\right)e^{-jn\omega _{0} t} dt$
$c_{n} $ komplex szám, amelyre fennáll a $c_{n} =\hat{c}_{-n} $ összefüggés, ahol $\hat{c}$ konjugált komplexet jelöl. Az $\omega =n\omega _{0} $ diszkrét frekvenciákhoz rendelt $c_{n} $ amplitúdók a periodikus $y\left(t\right)$ jel amplitúdó spektrumát alkotják.
A 2. ábra egy periodikus négyszögjelet szemléltet, amely frekvenciaspektrumával jellemezhető, vagyis közelíthető megadott frekvenciájú szinuszos jelek összegeként. A különböző frekvenciájú összetevők adott amplitúdóval jelennek meg. Ezek megadják a jel Fourier sorát, A 3. ábra mutatja, hogy a szinuszos összetevők számának növelésével a négyszögjel közelítése egyre jobb.
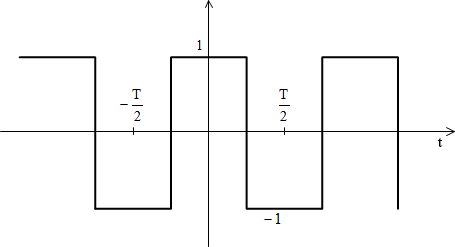
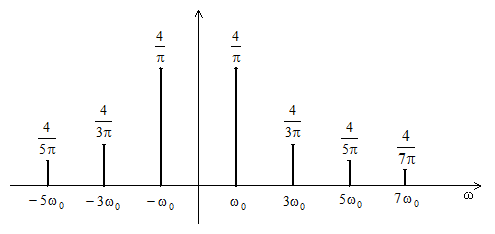
2. ábra Négyszögjel és spektruma
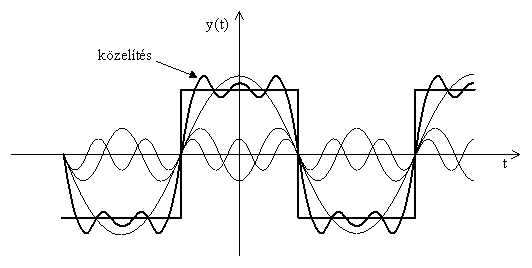
3. ábra Több szinuszos (Fourier) összetevővel a négyszögjel közelítése egyre jobb
Ha a periódusidő nő, a spektrumvonalak közelebb kerülnek egymáshoz (4. ábra). Ha a periódusidő végtelenhez tart, a jel aperiodikussá, és a frekvenciaspektrum folytonossá válik, vagyis a jel összetevőjeként minden frekvenciájú szinuszos jel szerepel. (A jelet ekkor a Fourier sor helyett a Fourier integrállal közelítjük.)
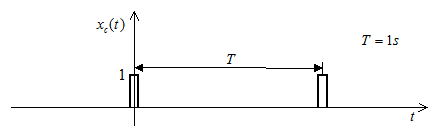
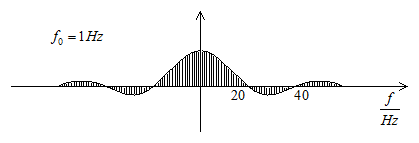
4. ábra Egy aperiodikus jel frekvenciaspektruma folytonos
A spektrumvonalak sűrűsödése, majd a spektrum folytonossá válása tanulmányozható az alábbi JAVA appleten.
Ha az aperiodikus függvény abszolút integrálható, vagyis fennáll az
$\int _{-\infty }^{\infty }\left|y\left(t\right)\right| \; dt=veges$
összefüggés, a függvény felírható a Fourier integrállal:
$y\left(t\right)=\frac{1}{2\pi } \int _{-\infty }^{\infty }Y\left(j\omega \right) e^{j\omega t} d\omega $
ahol $Y\left(j\omega \right)$ az ún. Fourier transzformált.
$Y\left(j\omega \right)=\int _{-\infty }^{\infty }y\left(t\right) e^{-j\omega t} dt$
(Látható a Fourier együtthatók és a Fourier transzformált közötti analógia.)
Ha negatív időkre $y(t)$ zérus,az integrálást 0-tól kezdjük, ekkor egyoldalas Fourier transzformáltról beszélünk.
Képezzük az $y\left(t\right)$ függvény $\dot{y}\left(t\right)$ idõ szerinti deriváltját.
$\dot{y}\left(t\right)=\frac{d y\left(t\right)}{dt} =\frac{1}{2\pi } \int _{-\infty }^{\infty }j\omega Y\left(j\omega \right) e^{j\omega t} d\omega $
A derivált függvény Fourier transzformáltja tehát az eredeti függvény Fourier transzformáltjából $j\omega $-val való szorzással kapható meg. A magasabb deriváltak az eredeti függvény Fourier transzformáltjának $j\omega $ megfelelõ hatványával való szorzásával kaphatók meg. Ezért ha képezzük egy differenciálegyenlet Fourier transzformáltját, algebrai egyenletet kapunk.
Egy lineáris rendszert gerjesszünk egy periodikus bemenőjellel. A lineáris rendszer alapvető tulajdonsága, hogy érvényes rá a szuperpozíció tétele, vagyis ha a bemenőjel különböző jelösszetevőkből áll, akkor a kimenőjel, ami a bemenőjelre adott válasz, az egyes bemenőjel összetevőkre adott válaszok összegével is megadható.
Az 5. ábra egy másodrendű differenciálegyenlettel megadható ún. kéttárolós lengő rendszer négyszög alakú periodikus bemenőjelét és annak 4 szinuszos összetevő jellel való közelítését, továbbá a bemenőjelre adott kimenőjelét és annak közelítését mutatja. A kimenőjel közelítését a 4 bemenőjel összetevőre adott válaszok összege adja. A 6. ábra a bemenőjel és a kimenőjel 10 összetevővel való közelítését mutatja. Látható, hogy 10 összetevővel mind a bemenőjel, mind pedig a kimenőjel közelítése jóval pontosabb, mint csupán 4 összetevő esetén.
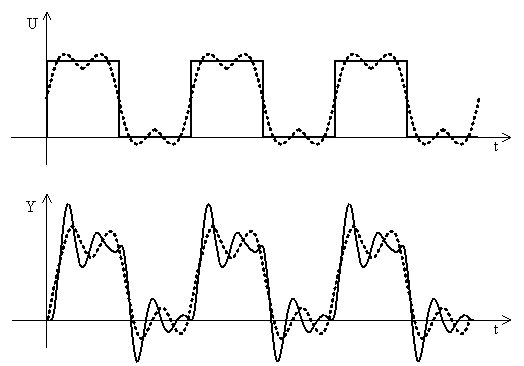
5. ábra Kéttárolós lengő tag bemenete és kimenete 4 Fourier összetevő esetén
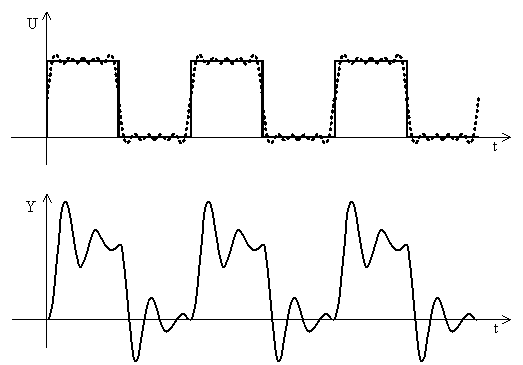
6. ábra Kéttárolós lengő tag bemenete és kimenete 10 Fourier összetevő esetén
Tehát mind a periodikus, mind pedig az aperiodikus jelek különböző frekvenciájú szinuszos jelek szuperpozíciójával adhatók meg. A periodikus jelek meghatározott diszkrét frekvenciájú szinuszos jelek összegével közelíthetők, ahol a magasabb frekvenciájú összetevők egyre kisebb amplitúdóval fordulnak elő. Az aperiodikus jelekben minden frekvencia előfordul adott súlyozással. Ha egy lineáris rendszert gerjesztünk egy jellel, amelyet különböző frekvenciájú szinuszos összetevőivel közelítünk, a szuperpozíció alkalmazásával a kimenőjel közelíthető a bemenőjel egyes összetevőire adott válaszok összegével. A közelítés annál jobb lesz, minél több frekvenciaösszetevőt veszünk figyelembe.
A fentiek alapján, ha egy lineáris rendszer szinuszos jelekre adott válaszait ismerjük, elvileg tetszőleges bemenőjelre adott időbeli válaszait is közelítőleg megadhatjuk.
Vizsgáljuk, hogyan válaszol a lineáris rendszer egy adott frekvenciájú szinuszos jelre (7. ábra). A kimenőjel egy ugyanolyan frekvenciájú szinuszos jel, amelynek amplitúdója és fáziseltolási szöge eltér a bemenőjelétől. A vizsgálatot (mérést) elvégezzük különböző frekvenciákra, a frekvenciát változtatjuk 0-tól $\infty $-ig. A kimenőjel amplitúdója és fázisszöge függ a frekvenciától. Megvárjuk, amíg a tranziensek lecsengenek, és csak az állandósult (kvázistacionárius) jeleket vizsgáljuk. A kimenőjelben a tranziensek azért alakulnak ki, mert a rendszernek tehetetlensége van, kimenőjele az első pillanatban nem változhat hirtelen.

7. ábra Egy lineáris rendszer válasza a szinuszos bemenőjelre
Ha minden frekvenciára meghatározzuk a szinuszos kimenőjel és szinusos bemenőjel maximális amplitúdóinak viszonyát és a fáziseltolási szöget, megkapjuk a frekvenciafüggvényt, amely a rendszer ismeretében analitikusan is megadható.
A frekvenciafüggvény többféleképpen is ábrázolható.
A Nyquist diagram a frekvenciafüggvényt a komplex számsíkon ábrázolja. A kiválasztott frekvenciatartomány minden egyes ${\omega }$ értékére a komplex síkban az $M\left(\omega \right)=A_{y} /A_{u} $ és $\varphi \left(\omega \right)$ értékpárnak megfelelő pontot adhatunk meg. Az adott pontot leírhatjuk valós és képzetes részével is. E pontok kontúrral való összekötése eredményezi a Nyquist diagramot. A Nyquist diagram ábrázolásakor a frekvenciát rendszerint nulla és végtelen között változtatjuk (8. ábra). A nyíl a frekvencia paraméter növekedésének irányát mutatja. A helygörbét sokszor kiegészítjük a negatív körfrekvenciákra számított értékekkel. Ilyenkor teljes Nyquist diagramról beszélünk. A görbe $-\infty <\omega <0$ tartományra megadott szakasza (az ábrán szaggatottan jelölve) a pozitív körfrekvenciákra számított görbe valós tengelyre vett tükörképe. Konkrét fizikai értelme csak a pozitív körfrekvenciának van. A Nyquist diagram alakja jellemzi a rendszert. Analizálva a Nyquist diagramot a rendszer fontos tulajdonságairól (például stabilitásáról, dinamikus tulajdonságairól) kaphatunk képet.
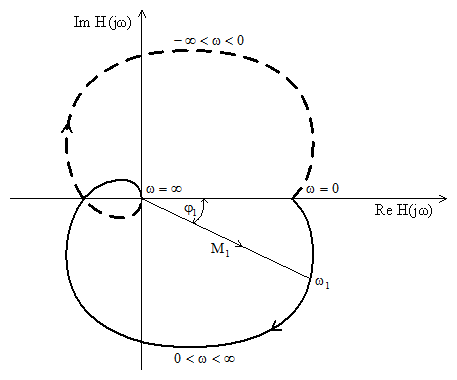
8. ábra Nyquist diagram
A Bode diagram a frekvenciafüggvény $\textit{M}(\textit{$\omega$})$ abszolút értékét és $\varphi \left(\omega \right)$ fázisszögét külön-külön ábrázolja a frekvencia függvényében egy kijelölt frekvenciatartományban (9. ábra). A frekvenciaskála léptéke rendszerint logaritmikus, így nagy frekvenciatartomány fogható át. Azt a frekvenciatartományt, amely alatt a frekvencia tízszeresére változik, 1 dekádnak nevezzük. (A zenében használatos oktáv olyan frekvenciasávot ad meg, amely alatt a frekvencia kétszeresére változik.) Az abszolút értéket vagy számértékével jellemezzük és logaritmikus skálában ábrázoljuk, vagy pedig – híradástechnikai hagyományokat követve – decibelben adjuk meg. A decibel (dB) a számérték 20-szoros logaritmusa. Ekkor a skála lineáris. A fázisszöget lineáris skálában ábrázoljuk.
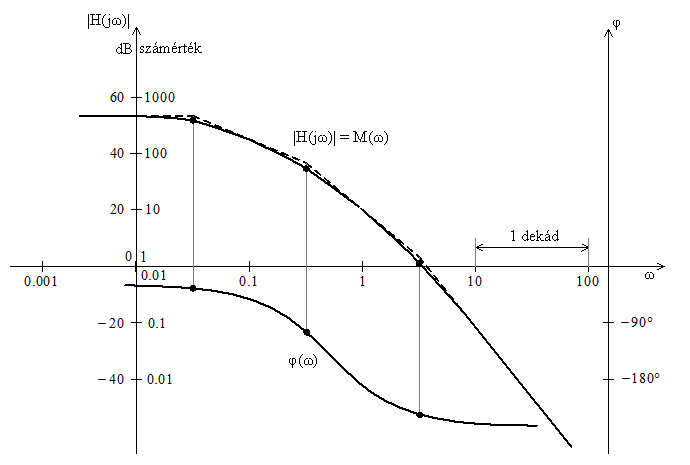
9. ábra Bode diagram
A Bode diagram egyik előnye, hogy rendszerint jól közelíthető aszimptotáival. A közelítő diagramok jellegéből és töréspontjaiból a rendszer tulajdonságairól gyors értékelést adhatunk.
Ha a rendszert olyan hatás éri, amely tranzienseket vált ki, kezdetben a nagyfrekvenciás, a későbbiekben pedig a kisfrekvenciás tulajdonságai dominálnak. A $j\omega \to 0$ átmenet éppen az állandósult állapotot adja meg. Tehát az átmeneti függvény (az ugrásválasz) értéke állandósult állapotban $(t\to \infty) $ megegyezik a frekvenciafüggvény $\omega =0$ értéknél felvett amplitúdójával. Az átmeneti függvény kezdeti értéke pedig a frekvenciafüggvény $\omega \to \infty $-nél felvett értékével azonos. A frekvenciafüggvény menete a középfrekvenciás tartományban a rendszer időbeli tranziens viselkedésével hozható kapcsolatba.
A frekvenciafüggvény menetéből, jellemzőiből tehát közelítő jellemzőket állapíthatunk meg az időfüggvényre, például a rendszer egységugrás válaszára. Ezek a közelítő összefüggések sokszor elegendőek a rendszer jellemzésére illetve a rendszerhez és a minőségi előírásokhoz a szabályozó tervezésére.
A frekvenciatartományban is megfogalmazhatjuk a követelményeket egy szabályozási rendszerrel szemben: „Milyen legyen a rendszer frekvenciafüggvénye (Nyquist vagy Bode diagramja), hogy a szabályozás kielégítse a vele szemben támasztott követelményeket? A negatívan visszacsatolt szabályozási körben milyen legyen a nyitott kör frekvenciadiagramja, hogy a zárt szabályozási kör stabilis legyen, megfelelő statikus és dinamikus tulajdonságokkal? Hogyan tervezzük meg a szabályozót az adott folyamathoz, amellyel a frekvenciadiagramot megfelelően formázhatjuk?” Ha a frekvenciatartományban megterveztük a szabályozót, a rendszer viselkedését az időtartományban vizsgáljuk.
A Fourier transzformáció alkalmazásának az abszolút integrálhatóság feltétele igen erős korlátot szab. Számos a gyakorlatban alkalmazott jelre, például az egységugrásra sem teljesül.
A gyakorlati alkalmazhatóság érdekében a Fourier transzformációt úgy kell módosítani, hogy alkalmazható legyen olyan jelekre is, amelyek nem abszolút integrálhatók.
Az egyoldalas Fourier transzformáció érvényességi köre nagymértékben kibővíthető, ha az $y\left(t\right)$ transzformálandó függvényt előzetesen megszorozzuk az $e^{-\sigma t} $ függvénnyel ($\sigma$>0), amely a függvények széles körére biztosítja az abszolút integrálhatóságot, majd az így kapott függvénynek határozzuk meg a Fourier transzformáltját. A szorzótényezővel módosított függvény Fourier transzformáltja az eredeti függvény Laplace transzformáltja.
A Laplace transzformált egyoldalas, a t = 0-ban kezdődő függvényekre:
$L\left\{y\left(t\right)\right\}=\int _{-\infty }^{\infty }y\left(t\right) \, e^{-\sigma t} e^{-j\omega t} dt=\int _{0}^{\infty }y\left(t\right)\, e^{-st} dt=Y\left(s\right) $
ahol az $s=\sigma +j\omega $ transzformációs változó pozitív valós részű komplex szám.
Tehát egy $y\left(t\right)$ függvény Laplace transzformáltja:
$Y\left(s\right)=\int _{0}^{\infty }y\left(t\right)e^{-st} dt $
Az inverz Laplace transzformált pedig:
$y\left(t\right)=\frac{1}{2\pi j} \int _{\sigma -j\infty }^{\sigma +j\infty }Y(s) e^{st} ds$
A Laplace operátortartományban is érvényes, hogy egy függvény időbeli deriváltjának Laplace transzformáltja a függvény Laplace transzformáltjának s-sel való szorzásával kapható meg. Pontosabban:
$L\left\{\dot{y}\left(t\right)\right\}=sY\left(s\right)-y\left(-0\right) $
$L\left\{\ddot{y}\left(t\right)\right\}=s^{2} Y\left(s\right)-sy\left(-0\right)-\dot{y}\left(-0\right)$
A számítás egyszerűsödik, ha a kezdeti feltételek zérus értékűek.
Ha a differenciálegyenletre alkalmazzuk a Laplace transzformációt, algebrai egyenletre jutunk. Zérus kezdeti feltételek mellett a deriváltak egyszerűen s megfelelő hatványával való szorzással adódnak. Az algebrai egyenletet megoldva megkapjuk a kimenőjel Laplace transzformáltját, majd inverz transzformációval visszatérünk az időtartományba.
Zérus kezdeti feltételek mellett a differenciálegyenletet a Laplace transzformált alakja:
$a_{n} s^{n} Y\left(s\right)+a_{n-1} s^{n-1} Y\left(s\right)+...+a_{1} sY\left(s\right)+a_{0} Y\left(s\right)=$
$b_{m} s^{m} U\left(s\right)+b_{m-1} s^{m-1} U\left(s\right)+...+b_{1} sU\left(s\right)+b_{0} U\left(s\right)$
A kimenőjel és a bemenőjel Laplace transzformáltjainak hányadosa a $H\left(s\right)$ átviteli függvény.
$H\left(s\right)=\frac{Y\left(s\right)}{U\left(s\right)} =\frac{b_{m} s^{m} +b_{m-1} s^{m-1} +b_{1} s+b_{0} }{a_{n} s^{n} +a_{n-1} s^{n-1} +...+a_{1} s+a_{0} } $
A számlálónak és a nevezőnek valós vagy konjugált komplex gyökei vannak. Jelöljük a számláló gyökeit – az átviteli függvény zérusait – $z_{1} ,z_{2} ,...,z_{m} $-mel, a nevező gyökeit – az átviteli függvény pólusait – pedig $p_{1} ,p_{2} ,...,p_{n} $-mel.
Az átviteli függvény gyöktényezős, zérus-pólus alakja:
$H\left(s\right)=k\frac{\left(s-z_{1} \right)\left(s-z_{2} \right)...\left(s-z_{m} \right)}{\left(s-p_{1} \right)\left(s-p_{2} \right)...\left(s-p_{n} \right)} $
Az átviteli függvény segítségével adott gerjesztésre a kimenőjel inverz Laplace transzformációval meghatározható.
Az átviteli függvény pólusai jellemzik a tranziens viselkedést. Valós pólusok aperiodikus, konjugált komplex pólusok lengő tranzienseket eredményeznek. Az origóba eső pólus integráló hatást jelent. A komplex számsík bal oldalára eső pólusok lecsengő, a jobb oldalra eső pólusok egyre növekvő amplitúdójú tranzienseket jelentenek.
Az átviteli függvény inverz transzformáltja, a súlyfüggvény a következő alakban adható meg:
$w\left(t\right)=L^{-1} \left\{H\left(s\right)\right\}=\alpha _{1} e^{p_{1} \, t} +\alpha _{2} e^{p_{2} \, t} +...+\alpha _{n} e^{p_{n} \, t} $
A pólusok a tranziensek lefolyását, a zérusok az egyes összetevők amplitúdóját befolyásolják.
A 10. ábra a pólusok komplex számsíkon való elhelyezkedésének és az időbeli tranziens viselkedésnek összefüggését szemlélteti.
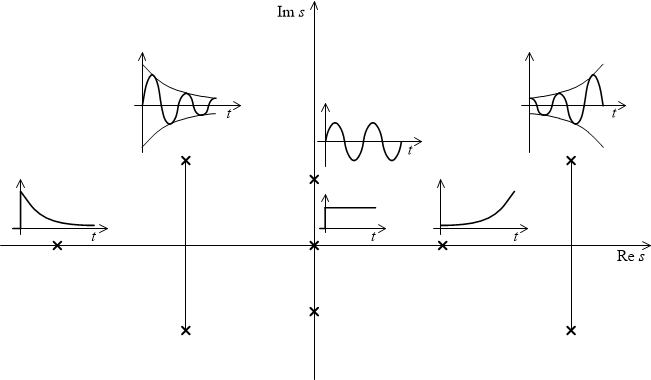
10. ábra A pólusok elhelyezkedése a komplex számsíkon meghatározza a dinamikus viselkedést
Az alábbi JAVA applet mutatja az átviteli függvényének számláló és nevező polinomjaival megadott rendszer átmeneti és súlyfüggvényét, valamint Bode és Nyquist diagramját.
Fodor György: A Laplace transzformáció műszaki alkalmazása. Műszaki Könyvkiadó, 1966.
Fodor György: Jelek és rendszerek, Műegyetemi Kiadó, 2006.
Keviczky, L., Bars, R., Hetthéssy, J., Barta, A., Bányász, Cs. Szabályozástechnika. Műegyetemi Kiadó, 55079, 2006, 2009.
Åström,K.J., Murray, R.M. Feedback Systems:
An Introduction for Scientists and Engineers. Princeton University Press, 2009. http://www.cds.caltech.edu/~murray/books/AM05/pdf/am08-complete_22Feb09.pdf
Szilágyi (1998)
