

A modellezésről és identifikációról
A modellezés absztrakciót igényel. A rendszert bizonyos szempontok alapján vizsgáljuk, míg más szempontokat figyelmen kívül hagyunk. A modellezés a rendszer természetének és működésének mély megértését és ennek matematikai formában való megfogalmazását jelenti. A rendszer dinamikus viselkedésének vizsgálata, illetve a rendszer irányítása szempontjából a jelátvitel a fontos, tehát az, hogy az adott bemenőjelre, bemenőjelekre a rendszer milyen kimenőjellel válaszol. Más szempontból fontos egyéb tulajdonságokat most figyelmen kívül hagyunk. A jelátvitel matematikai egyenletekkel, rendszerint differenciálegyenletekkel vagy differenciaegyenletekkel írható le. A rendszer megvalósításakor természetesen más szempontok is előtérbe kerülnek, fontos például a rendszer alkotóelemeinek kiválasztása, realizálása, a berendezések mérete és ára, környezetvédelmi szempontok, stb.
A felhasznált információ forrása lehet a priori: ilyen például az előzetes elemzés, a kapcsolatok feltárása, a modellezés céljának és a pontossági igényeknek meghatározása, a modell típusának megválasztása. A rendszer jelátviteli tulajdonságai a fizikai (biológiai, gazdasági, stb.) működést leíró matematikai összefüggésekkel adhatók meg. A fizikai működés mély megértése szükséges a matematikai leíráshoz. A matematikai egyenletekben szereplő paraméterek értékei számítással vagy méréssel határozhatók meg. Egy rendszer statikus és dinamikus viselkedése meghatározható a bemenőjelek és a hatásukra létrejövő kimenőjelek elemzésével is.
A jelátviteli tulajdonságokat leíró matematikai modellt egy dobozzal adhatjuk meg, a dobozba mutató nyíl a bemenőjelet jelzi, a dobozból kifelé mutató nyíl a kimenőjelet jelenti. A dobozba beírjuk a jelátvitelt jellemző matematikai összefüggést.
Amikor a teljes modellt a priori ismeretek alapján állítjuk fel, amik lehetnek fizikai elvek (Newton, Hamilton, Lagrange formalizmus, megmaradási elvek, mérlegegyenletek), akkor fehér doboz (white-box) modellezésről beszélünk. A módszer előnye, hogy a modell fizikai paramétereinek valós tartalma, jelentése van, hátránya viszont, hogy a modell felépítése általában rendkívül bonyolult. Ezen túlmenően a modell-bizonytalanságok kezelése is eléggé problematikus.
Ha az információ forrása a posteriori, akkor a feladat a rendszerről megfigyelések és mérések által gyűjtött információ alapján a modell megalkotása és pontosítása, illetve a modell megbízhatósági/érvényességi tartományának vizsgálata. Általában ekkor beszélünk modell identifikációról és validációról. Amikor a struktúra nem, vagy csak részben adott, struktúra-identifikációról, míg ha a struktúra adott, akkor paraméter-identifikációról beszélünk.
Ha a rendszerre üzem közben nem adható vizsgálójel, az identifikációhoz az üzemeltetés közben mérhető jeleket használjuk fel. Ha azonban a rendszer bemenetéhez hozzáférhetünk, célszerű a kísérlethez a bemenőjelet megfelelően megválasztani. Az eljárás feltételezi a rendszer modelljének valamilyen alakját, és a modell paramétereit úgy határozza meg, hogy a rendszer és a modell kimenőjelei minél jobban illeszkedjenek egymáshoz.
Mivel a paraméterek értékeit rendszerint mérés útján határozzuk meg, értékük nem egészen pontos, de többnyire megadható a paraméterbizonytalanságok értéke, a paraméterek értékeinek figyelembe veendő tartománya.
A fehér doboz modellezés ellenpontja a fekete doboz (black-box) modellezés, amikor is a modell felállításához csak kísérletekkel, mérésekkel lehet információkat szerezni. Ilyen információ forrása lehet például a vizsgálójelekre adott rendszerválaszok (például az egységugrásra adott válasz, az ún. átmeneti függvény) elemzése. Elsősorban lineáris időinvariáns (LTI) rendszermodellek esetén használatos. A fekete doboz modellek lényeges előnye viszonylagos egyszerűségük; hátrányuk viszont, hogy a paramétereknek általában nincs valós fizikai jelentése.
Ebben az esetben a rendszer modelljének konstruálása a bemenőjelek és a kimenőjelek mért (mintavételezett) adatai alapján történik (1. ábra).
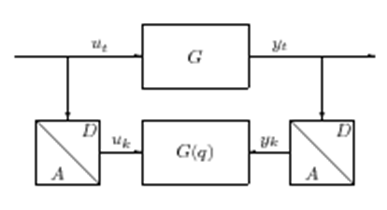
1. ábra Identifikálandó modell
A rendszeridentifikáció végrehajtása több lépésben történik:
- A bemenő- és kimenőjelek mérése, mintavételezése, szűrése, feldolgozása;
- A modell struktúrájának megadása fizikai megfontolások alapján;
- A modell paramétereinek becslése;
- A modell ellenőrzése, tesztelése, validálása;
- A diszkrét modell transzformálása folytonos alakra.
E két véglet között helyezkedik el a szürke doboz (grey-box) modellezés, ami az előző két módszer kombinációja. Főleg nemlineáris jelenségek modellezésére használatos. Ekkor a struktúra adott - de nem feltétlenül valamiféle egzakt levezetés eredménye. A nemlinearitások leírásakor gyakran heurisztikus ismeretek épülnek be a modellbe. A műszaki gyakorlatban legtöbbször ez az eset fordul elő. Hátránya az, hogy a struktúra és a parametrizálás általában nem örződik meg a szokásos diszkretizálási eljárásokban.
A fizikai modellezést és az identifikációt rendszerint együttesen alkalmazzuk (2. ábra).
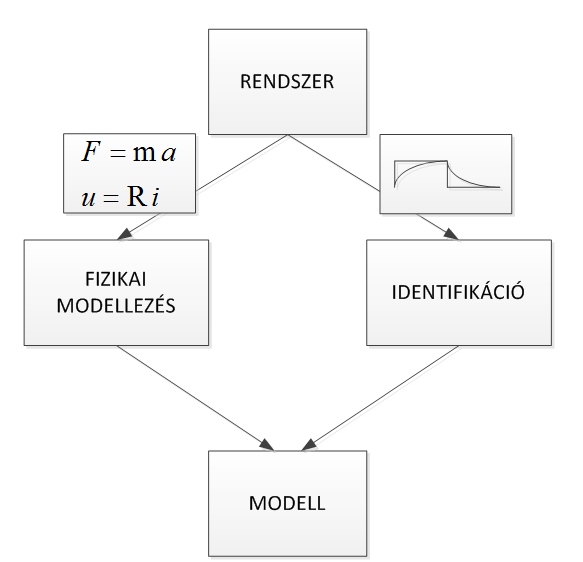
2. ábra A fizikai modellezést és az identifikációt rendszerint együttesen alkalmazzuk
A modell akkor megbízható, ha kimenőjele egy adott bemenőjelre jól közelíti a rendszer tényleges kimenőjelét. A modellnek megadható az érvényességi tartománya (például a bemenőjelnek mely tartományában érvényes).
A rendszer modellje lehet a rendszer statikus karakterisztikáját megadó görbe, amely a kimenőjel és a bemenőjel állandósult értékei közötti összefüggést adja meg, vagy egy tipikus rendszerválasz időfüggvénye, például az egységugrásra adott válasz, az ún. átmeneti függvény, amely sokszor egyszerűen mérhető. Általában differenciálegyenlet írja le az összefüggést az $u(t)$ bemenőjel és az $y(t)$ kimenőjel között, amely megadja a kapcsolatot a kimenőjel és annak kis megváltozásai (deriváltjai) és a bemenőjel és deriváltjai között. Lineáris rendszerek esetén a differenciálegyenlet Laplace transzformáltját képezve algebrai egyenletet kapunk. A kimenőjel és a bemenőjel Laplace transzformáltjainak hányadosa a $P(s)$ átviteli függvény. Sokszor a jelátvitelt a dobozba beírt átviteli függvénnyel jellemezzük (3. ábra). Az n-edrendű differenciálegyenlet átírható n darab elsőrendű differenciálegyenlet rendszerévé, az ún. állapotegyenletté.
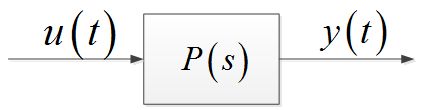
3. ábra A jelátvitelt sokszor az átviteli függvénnyel jellemezzük
Néhány fontos rendszertulajdonság, amely a kimenőjel és a bemenőjel kapcsolatát jellemzi a linearitás, a kauzalitás és az időinvariancia.
Linearitás: A rendszerre alkalmazható a szuperpozíció elve. Ha a rendszer az $u_1$ bemenőjelre $y_1$, az $u_2$ bemenőjelre pedig $y_2$ kimenőjellel válaszol, akkor az $\alpha u_1+\beta u_2$ bemenőjelre a rendszer válasza $\alpha y_1+\beta y_2$, ahol $\alpha$ és $\beta$ konstansok.
Kauzalitás: A kimenőjel egy adott időpontban a bemenőjel múltbeli értékeitől és aktuális értékétől függ. Nem függ a bemenőjel jövőbeni értékeitől.
Időinvariancia: Egy rendszer időinvariáns, ha a bemenőjelre adott válasza nem függ a bemenőjel belépésének időpontjától; egy $\tau$ idővel késleltetett adott bemenőjelre ugyanazt a választ adja $\tau$ időeltolással. Az időinvariáns rendszerben a késleltetett kimenetre fennáll, hogy $y_\tau (t)=y(t-\tau )$.
A leggyakrabban alkalmazott lineáris rendszermodellek az n-edrendű differenciálegyenlet, az átviteli függvény és az állapottér modell. A átviteli függvény a kimenőjel és a bemenőjel Laplace transzformáltjainak hányadosa. Az állapottér modell a bemenőjelek, az állapotváltozók és a kimenőjelek között adja meg a kapcsolatot. Az állapotváltozók a rendszer belső változói, amelyek pillanatnyi értéke a rendszer korábbi mozgása révén jött létre. Értékük nem változhat hirtelen a bemenőjelek hirtelen változásakor. A bemenőjelek és az állapotváltozók pillanatnyi értéke meghatározza a rendszer további mozgását.
Egy n-edrendű differenciálegyenlet n számú elsőrendű differenciálegyenlet rendszerévé alakítható át.
$\dot{x} (t)=Ax(t)+bu(t)$
$y(t)=c^Tx(t)+du(t)$
ahol $x$ a belső változók vektora, az ún. állapotvektor és $\{A,b,c,d\}$ a rendszert jellemző paramétermátrixok.
Diszkrét idejű mintavételezett rendszereknél a bemenő és kimenőjelekből, illetve az állapotváltozókból mintákat veszünk, a rendszermodellek az impulzusátviteli függvénnyel illetve a diszkrét állapotegyenlettel írhatók le, ahol matematikailag a z-transzformációt alkalmazzuk.
Mintavételezett lineáris rendszer identifikációját az 53. oldalon tárgyaljuk.
Hivatkozások:
Ljung (1999)