

A blokkdiagramokról
A rendszert a jelátvitel szempontjából egy dobozzal, blokkal jellemezhetjük. A dobozba irányuló nyíl a bemenőjelet jelenti, amely a környezetből jövő hatást adja meg. A dobozból kifelé mutató nyíl a kimenőjelet szimbolizálja, azt mutatja, hogyan hat a rendszer a környezetére, hogyan válaszol a bemenőjelre. A dobozba berajzolhatunk egy a jelátvitelt jellemző függvényt, vagy a dobozba beírjuk a jelátvitelt jellemző matematikai összefüggést (1. ábra). A rendszer jelátviteli tulajdonságait jellemző dobozt jelátviteli tagnak is nevezzük. Ez a jelátviteli tag a rendszer modellje.

1. ábra Jelátviteli tag
Tagok alapkapcsolásai
A rendszerek különböző módokon kapcsolódhatnak egymáshoz. A kapcsolódás módja az ún. blokkvázlattal fejezhető ki, amely megadja a tagok egymásra hatását.
A jelátviteli tagok három alapvető kapcsolása a soros kapcsolás, a párhuzamos kapcsolás és a visszacsatolás.
Jelöljük az egyes tagok jelátviteli függvényeit $H$-val. Az $y$ kimenőjelet megkapjuk, ha az $u$ bemenőjelre alkalmazzuk a $H$ operátort, $y=Hu$. (A későbbiekben (50. oldal) belátjuk, hogy a szorzási összefüggés érvényes a Laplace operátortartományban.)
Fontos lehet a kapcsolt eredő rendszer viselkedésének vizsgálata, illetve az összetevő részrendszerek viselkedésének vizsgálata is.
Soros kapcsolás
A soros kapcsolásnál az egyik tag kimenőjele a másik tag bemenőjele (2. ábra).

2. ábra Soros kapcsolás
Az eredő átvitelt az alábbi összefüggéssel határozhatjuk meg:
$Y(s)=Y_1(s) H_2(s) = U(s) H_1(s) H_2(s)$
Az eredő átviteli függvény tehát az egyes összetevő tagok átviteli függvényeinek szorzata.
$H(s)=H_1(s) H_2(s)$
Párhuzamos kapcsolás
Párhuzamos kapcsolásnál a tagok bemenőjele azonos, kimenőjeleik összegződnek (3. ábra).
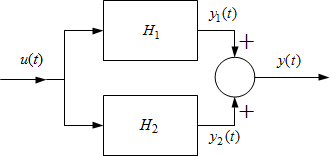
3. ábra Párhuzamos kapcsolás
Az eredő átvitelt az alábbi összefüggéssel határozhatjuk meg:
$Y(s)=Y_1(s)+Y_2(s)=U(s)(H_1(s)+H_2(s))$
Az eredő átviteli függvény tehát az egyes összetevő tagok átviteli függvényeinek összege.
$H(s)=H_1(s) + H_2(s)$
Visszacsatolás
Visszacsatolásról beszélünk, ha valamely tag kimenőjelét – egy másik tagon keresztül vezetve – a bemenőjeléhez hozzáadjuk vagy kivonjuk. Az előbbi esetet pozitív, az utóbbit negatív visszacsatolásnak nevezzük.
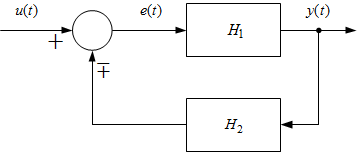
4. ábra Visszacsatolás
A rendszerek szabályozásakor az alapkapcsolás a negatív visszacsatolás, amikor a rendszerbe az alapjel és az érzékelt kimenőjel különbsége alapján avatkozunk be.
Az eredő átvitelt a jelek hatásának vizsgálatával az alábbi összefüggésekkel határozhatjuk meg:
$Y(s)=E(s)H_1(s)=(U(s)-H_2(s)Y(s))H_1(s)$
Átrendezve: $Y(s)=\frac{H_1(s)}{1+H_1(s)H_2(s)}U(s)$
Az eredő átviteli függvény:
$H(s)=\frac{H_1(s)}{1 \pm H_1(s)H_2(s)}$
A nevezőben a negatív előjel a pozitív visszacsatolásra vonatkozik.
Az $L(s)=H_1(s)H_2(s)$ függvényt hurokátviteli függvénynek nevezzük.
Az összefüggés negatív visszacsatolásra érvényes, pozitív visszacsatolásnál a nevezőben az előjel negatív.
Negatív visszacsatolásnál tehát az eredő átvitel az előrevezető ág átviteli függvényének és az ún. hurokátviteli függvény 1-gyel megnövelt értékének hányadosa.
Az 5. ábra példaként a tagok egy összetettebb kapcsolását mutatja. Itt is megadható az $y$ kimenőjel és az $u$ bemenőjel közötti eredő jelátviteli összefüggés, amely figyelembe veszi az egyes részrendszerek kapcsolódásából eredő hatásokat.
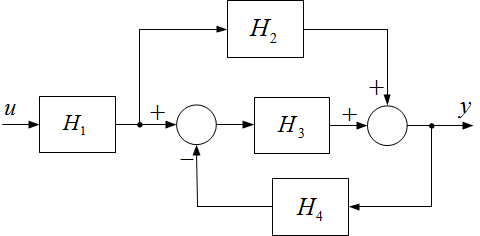
5. ábra A jelátviteli tagok összetettebb kapcsolódása határozza meg az eredő jelátviteli kapcsolatot
A blokkvázlat egyenértékű átalakítása segíthet az eredő meghatározásában.
Hivatkozások:
Keviczky et al. (2009,2011)