

Robusztus stabilitás, robusztus performancia
Mivel a rendszerre ható külsĹ körülmények változhatnak, valamint az érzékelĹk és beavatkozó szervek tulajdonságai is módosulhatnak, kisebb hibák léphetnek fel ezért növelni kell a szabályozó robusztusságát ezekre a tényezĹkre és a modellezési hibákra.
A szabályozási feladatot az ábrán bemutatott $P-K-\Delta$ struktúrában fogalmazzuk meg amit az alábbi egyenletek írnak le
$$
\begin{pmatrix} \eta \\ z\\ y \end{pmatrix}=
P \begin{pmatrix} \xi \\ w\\ u \end{pmatrix}=
\begin{pmatrix}
P_{11} & P_{12} & P_{13}\\
P_{21} & P_{22} & P_{23}\\
P_{31} & P_{32} & P_{33}
\end{pmatrix}
\begin{pmatrix} \xi \\ w\\ u \end{pmatrix}.
$$
ahol $\eta,\ \xi$ jelek a bizonytalanságok leírására szolgálnak, $w,\ z$ az általánosított rendszerstruktúra zavarás és performancia jelei, $u,\ y$ a szabályozó bemenet és a mért kimenet.
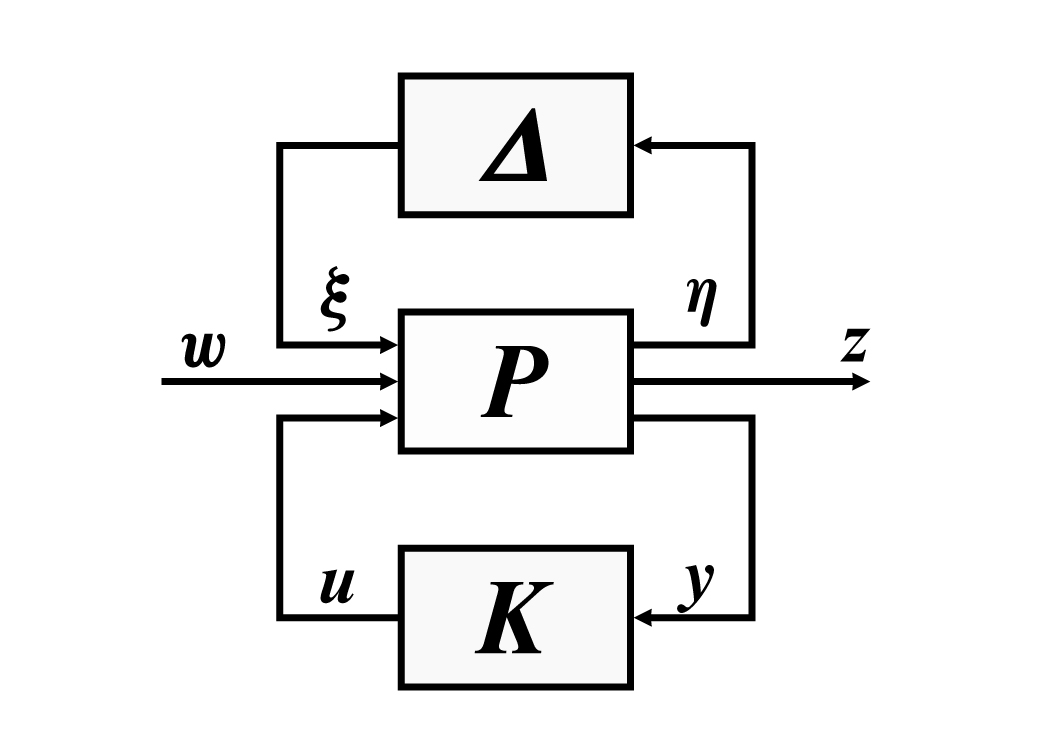
$P-K-\Delta$ struktúra
A bizonytalansági halmaz, $\Delta$, stabil átmenetfüggvényekbĹl áll. A perturbált kör a
$$
\xi = \Delta \eta
$$
bizonytalanság hatására alakul ki:
$$
\begin{pmatrix} \eta \\ z \end{pmatrix}=
\mathcal{F}_u(P, \Delta)\begin{pmatrix} w\\u \end{pmatrix}=
\begin{pmatrix} P_{22} & P_{23}\\ P_{32} & P_{33} \end{pmatrix}+
\begin{pmatrix} P_{21}\\ P_{31} \end{pmatrix}
\Delta(I-P_{11}\Delta)^{-1}
\begin{pmatrix} P_{12} & P_{13} \end{pmatrix}
\begin{pmatrix} w\\u \end{pmatrix}.
$$
Az $u=Ky$ szabályozót a nominális (perturbálatlan) rendszerre kötve kapjuk, hogy
$$
\begin{pmatrix} z\\ y \end{pmatrix}=
\mathcal{F}_l(P, K)\begin{pmatrix} \xi \\w \end{pmatrix}= \begin{pmatrix} P_{11} & P_{12}\\ P_{21} & P_{22} \end{pmatrix}+
\begin{pmatrix} P_{13}\\ P_{23} \end{pmatrix}
K(I-P_{33}K)^{-1}
\begin{pmatrix} P_{31} & P_{32} \end{pmatrix}
\begin{pmatrix} \xi \\w \end{pmatrix}.
$$
A szabályozott, $u=Ky$, és perturbált, $\xi=\Delta \eta$, kör alakja
$$
\mathcal{F}_u(\mathcal{F}_l(P, K), \Delta)=
\mathcal{F}_l(\mathcal{F}_u(P,\Delta), K).
$$
Mivel a zárt körnek jól definiáltak kell lenni és nem függhet $\Delta$ és $K$ sorrendjétĹl, néhány feltételezéssel kell élnünk:
- Létezik $u=Ky$ szabályozó, ami stabilizálja a nominális ($\Delta=0$) rendszert ($P$).
- A bizonytalansági halmaz
$$\Delta=\{\Delta(s)\in \mathcal{RH}_{\infty} \ | \ \Delta(i\omega)\in\Delta_{c} \textrm{ minden } \omega\in \mathbb{R}\cup\{\infty\}\textrm{ esetén } \}, $$
ahol $\Delta_{c}$ komplex mátrixok egy halmaza, ami tartalmazza $0$-t, ami meghatározza a bizonytalanságok méretét és struktúráját. Feltesszük, hogy ez a halmaz csillag alakú, vagyis $\Delta \in\Delta_{c} \Rightarrow \tau\Delta\in\Delta_{c}$ minden $\tau\in[0,1]$ esetén. - A bizonytalanságok és az általánosított rendszerstruktúra kötése jól definiált, vagyis $I -P_{11}(\infty)\Delta_{c}$ invertálható minden $\Delta_{c}\in\mathbf{\Delta}_{c}$ esetén.
Ezek a feltételek jórészt automatikusan teljesülnek a szokásos, intervallum, gömb, stb. típusú bizonytalansági halmazokra.
Általában normalizáló súlyozásokat alkalmazunk, amit azután figyelembe veszünk $P$ összeállításánál: ha $\hat{\Delta}$ bizonytalansággal akarunk dolgozni, ahol $\Delta=W_{1}\hat{\Delta} W_{2}$ valós racionális $W_{1}$ és $W_{2}$ súlyokkal, akkor $P$ helyett $\hat{P}$ rendszert kell tekintenünk, ahol
$$
\hat{P}=\begin{pmatrix}
W_{2}P_{11}W_{1} & W_{2}P_{12} & W_{2}P_{13}\\
P_{21}W_{1} & P_{22} & P_{23}\\
P_{31}W_{1} & P_{32} & P_{33}
\end{pmatrix}.
$$
Robusztus stabilitás vizsgálat
Vezessük be a
$$
\mathcal{F}_l(P,K)=
\begin{pmatrix}
M & N_{12}\\ N_{21} & N_{22}
\end{pmatrix},
$$
jelölést, ahol $M$ a bizonytalanság által látott átviteli függvény.
Ha $K$ stabilizálja $P$-t és ha $I -M\Delta$ minden szóba jöhetĹ $\Delta$ esetén stabilan invertálható akkor $K$ robusztusan stabilizálja $\mathcal{F}_u(P,\Delta)$-t a $\Delta$ bizonytalanságra nézve.