

Állapotvisszacsatolás, állapotbecslés
Ha a rendszert állapotmodelljével, állapotegyenletével írjuk le, olyan szabályozási algoritmust keresünk, amely ebből a rendszermodellből indul ki.
Rudolf Kalman az 1960-as években az állapotvisszacsatoláson alapuló szabályozási algoritmust javasolta. valamennyi állapotváltozót érzékeljük, mérjük, és a rendszer beavatkozójelét az állapotváltozók konstanson keresztül történő negatív visszacsatolásával képezzük.
$u=-k^{{\rm T}} x.$
Az állapotvisszacsatolás megváltoztatja a rendszer dinamikáját. Ha például egy egytárolós arányos tagot, amelynek kimenete állapotváltozó, negatívan visszacsatolunk egy konstanssal, a rendszer felgyorsul (dinamikája egytárolós arányos jellegű marad, időállandója kisebb lesz, de átviteli tényezője is lecsökken).
Az állapotváltozók visszacsatoló konstansait úgy kell megválasztani, hogy a rendszer egy előírt mértékben felgyorsuljon. Előírhatjuk, hova kívánjuk eltólni a zárt rendszer pólusait a folyamat pólusaihoz képest. Minél inkább balra helyezkednek el a pólusok a komplex számsíkon, annál gyorsabb lesz a zárt szabályozási rendszer. Az állapotvisszacsatoló konstansok egy kvadratikus célfüggvény minimalizálásával is meghatározhatók (LQ probléma).
Mivel ez a szabályozási algoritmus nem hoz be integráló hatást a szabályozási körbe, lesz állandósult állapotbeli eltérés az alapjel követésében, illetve a zavarások elhárításában. Statikus kompenzációval kell gondoskodni az állandósult állapotbeli hibák kiküszöböléséről, illetve a struktúrába mesterségesen be kell iktatni integrátort, amelynek kimenőjele egy járulékos állapotváltozó.
Egy másik probléma, hogy sokszor nem valamennyi állapotváltozó hozzáférhető, mérhető. Az állapotváltozók értékei sokszor zajokkal terheltek. Ekkor az állapotváltozókat becsülni kell, a zajokat ki kell szűrni, és az állapotvisszacsatolást a becsült állapotváltozókról kell létrehozni.
Kálmán-szűrő
A Kálmán szűrő a változásokat követő szabályozások legjobban elterjedt megoldása. A szűrő érzékeli a rendszer pillanatnyi állapotát, képünkön egy repülő test viszonyait és a következő lépésekben (pld. mintavételekben) valószínűségi becslést végez az új állapot és a korábbi becslés között. Ez a folyamat kiszűri a zavaró érzékeléseket és a becslés megadja a rendszer pillanatnyi állapotát.
Tekintsük először a folytonos rendszereket. Egy folytonos, lineáris, időinvariáns, egy bemenetű/egy kimenetű rendszer állapotteres reprezentációja az $A,b,c,d$ paramétermátrixokkal írható le:
$\begin{array}{l} {\dot{x}=Ax+bu} \\ {y=c^{{\rm T}} x+du} \end{array}$
(A felső T index jelöli, ha sorvektorról van szó.)
A fenti egyenletek (nevezetesen az állapotegyenlet illetve a kimeneti egyenlet) az bemenet és az kimenet között a
$P(s)=\frac{Y(s)}{U(s)} =c^{T} (sI-A)^{-1} b+d$
átviteli függvényt valósítják meg.
A modell pólusait a
${\rm det}(sI-A)=0$
karakterisztikus egyenlet gyökei határozzák meg. Megjegyezzük, hogy a gyakorlati esetek nagy részében $d=0$.
Állapotvisszacsatolás
Az állapotvisszacsatolás a beavatkozójelet az állapotváltozóknak a $k^{{\rm T}} $vektor konstans elemeivel való visszacsatolásával képzi:
$u=-k^{{\rm T}} x.$
A rendszer állapotváltozóiról megvalósított, az 1. ábrán bemutatott visszacsatolás az r referenciajel (alapjel) és az y kimenőjel közötti átvitelt mind statikus, mind pedig dinamikus értelemben módosítja.
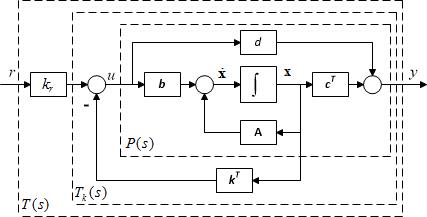
1. ábra Állapotvisszacsatolásos szabályozás vázlata
A visszacsatolásban $k^{{\rm T}} $visszacsatoló (sor)vektort, az előrevezető ágban $k_{{\rm r}} $ erősítési ún. kompenzációs tényezőt feltételezve a visszacsatolt (zárt) rendszer egyenletei $u=k_{{\rm r}} r-k^{{\rm T}} x$ következtében az alábbiak szerint írhatók fel (itt a d paramétert is figyelembe vesszük, amelynek értéke rendszerint zérus):
$ {\dot{x}=(A-b k^{{\rm T}} )x+k_{r} br} \\ {y=(c-dk^{{\rm T}} )x+dk_{r} r} $
Bevezetve az $A_{k} =A-b k^{{\rm T}} ,\, \, b_{k} =k_{r} b,{\rm \; }c_{k} =c-dk,{\rm \; }d_{k} =dk_{r} $ jelöléseket
$\begin{array}{l} {\dot{x}=A_{k} x+b_{k} r} \\ {y=c_{k}^{{\rm T}} x+d_{k} r} \end{array}$
adódik a zárt rendszerre, amelynek karakterisztikus egyenlete:
${\rm det}(sI-A_{k} )={\rm det}(sI-A+bk^{{\rm T}} )=0.$
A nyitott és zárt rendszer karakterisztikus egyenletét összevetve látható, hogy a nyitott rendszer pólusai csak A értékétől, míg a zárt rendszer pólusai az $\left\{A,b,k^{{\rm T}} \right\}$ hármastól függenek. A zárt rendszer tulajdonságait úgy tervezzük meg, hogy előírjuk, hová kerüljenek a zárt rendszer pólusai a komplex síkban. Matematikailag olyan $k^{{\rm T}} $ visszacsatoló vektort keresünk, amely a karakterisztikus egyenlet gyökeit éppen e kívánt értékekre helyezi el.
Az állapotvisszacsatolásos rendszer tervezése az alábbi lépésekben történik:
- válasszuk meg a zárt rendszer előírt pólusait;
- egy bemenetű/egy kimenetű rendszerek esetén a visszacsatoló vektort úgy választjuk meg, hogy a pólusok az előírt értékekre kerüljenek (Ackermann formula)
- az állandósult állapotbeli átvitelre megfogalmazott követelmények alapján határozzuk meg a statikus kompenzációs tényezőt.
Állapotbecslés
A gyakorlati alkalmazások döntő részében a folyamatok műszerezése magába foglalja a rendszer kimenetének mérését, azonban az állapotváltozók közvetlen méréssel rendszerint nem hozzáférhetők. Ilyen esetekben az állapotvisszacsatolásos szabályozási technika alkalmazhatóságát a nem mért állapotváltozók becslése kell, hogy kiegészítse. Az állapotváltozók becslésére szolgáló ún. megfigyelő (Kalman szűrő) blokkvázlata a 2. ábrán látható. A szűrő megbecsüli a rendszer pillanatnyi állapotait és kiszűri a zavarásokat is. A megfigyelő részét képező modell felépítése követi a rendszer felépítését. Feltételezzük, hogy $d=0$. Ha a rendszer ismert, a modell paramétermátrixai megegyeznek a rendszer paramétermátrixaival. A rendszer és a modell kimenetének különbsége egy hibajelet állít elő. E hibajelnek a modellbe történő visszacsatolása módosítja a becsült állapotváltozók deriváltját biztosítva azt, hogy a modell becsült állapotváltozóinak mozgása minél kisebb hibával kövesse (másolja le) a rendszer állapotváltozóinak mozgását. A becslő hálózat egy zárt kört alkot, amelynek bemenőjele a folyamat y kimenőjele. A becslő hálózat pólusai előírhatók. Lényeges szempont, hogy a becslő hálózat dinamikája legyen jóval gyorsabb a folyamat dinamikájánál. A becslő hálózat L erősítési vektora ismét az Ackermann formulával számítható. Az ábrán látható, hogy a becslő kör viselkedését az A és a $c^{{\rm T}} $ paramétermátrixok befolyásolják.
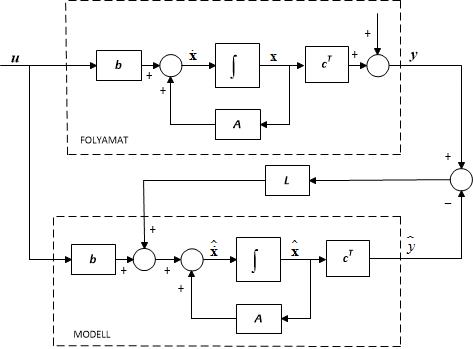
2. ábra Állapotbecslés
A 3. ábra példaként szemlélteti, hogy az állapotváltozó becsült értéke rááll a tényleges értékére.
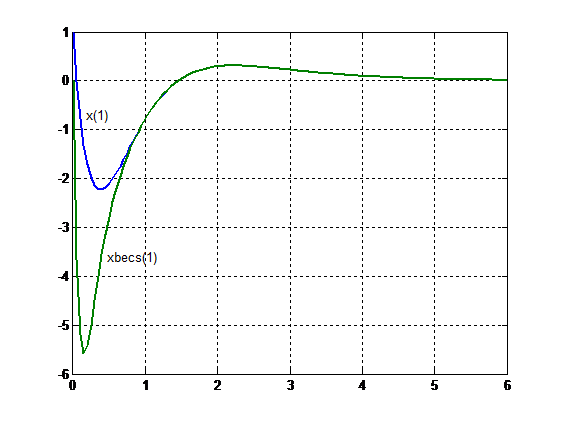
3. ábra Példa az állapotbecslésre: az x(1) becsült értéke a becslés tranziensének lezajlása után rááll a tényleges értékre
Állapotvisszacsatolás a becsült állapotváltozókról
Az állapotbecslés és állapotvisszacsatolás egymástól függetlenül elvégezhető feladatok. Ha az állapotváltozók nem hozzáférhetők, az állapotvisszacsatolásos szabályozást a becsült állapotváltozók visszacsatolásával valósíthatjuk meg azzal a k visszacsatoló vektorral, amellyel a hozzáférhető állapotváltozókat csatolnánk vissza. Lényeges szempont, hogy a folyamat dinamikájánál az állapotvisszacsatolt rendszer dinamikája legyen gyorsabb, és a becslő hálózat dinamikája az állapotvisszacsatolt rendszerénél is legyen gyorsabb, hogy az állapotvisszacsatolás a rendszer állapotváltozóit gyorsan és jól közelítő becsült állapotváltozókról történjen.
A szabályozás blokkvázlatát a 4. ábra adja meg.
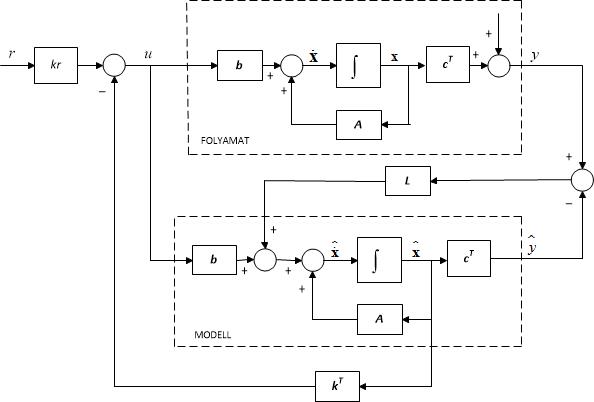
4. ábra Állapotvisszacsatolás a becsült állapotváltozókról
Az ábra alapján a rendszer állapotegyenlete:
$\left[\begin{array}{c} {\dot{x}} \\ {\dot{\hat{x}}} \end{array}\right]=$$
\left[\begin{array}{cc} {A} & {-bk^{{\rm T}} } \\ {Lc^{{\rm T}} } & {A-Lc^{{\rm T}} -bk^{{\rm T}} } \end{array} \right] $ $\left[\begin{array}{c} {x} \\ {\hat{x}} \end{array}\right]+\left[\begin{array}{c} {bk_{r} } \\ {bk_{r} } \end{array}\right]r$
${y=\left[\begin{array}{cc} {c^{{\rm T}} } & {0} \end{array}\right]\left[\begin{array}{c} {x} \\ {\hat{x}} \end{array}\right]+0\cdot r }$
Az állapotbecslés és állapotvisszacsatolás mintavételes rendszerekben is elvégezhető.
Hivatkozások
Åström,K.J., Murray, R.M. Feedback Systems: An Introduction for Scientists and Engineers. Princeton University Press, 2008.
Keviczky, L., Bars, R., Hetthéssy, J., Barta, A., Bányász, Cs. Szabályozástechnika. Műegyetemi Kiadó, 55079, 2009.
Hetthéssy, J., Bars, R., Barta, A. Szabályozástechnika, MATLAB gyakorlatok, BME Viking Zrt, VI 201-040, 2014.