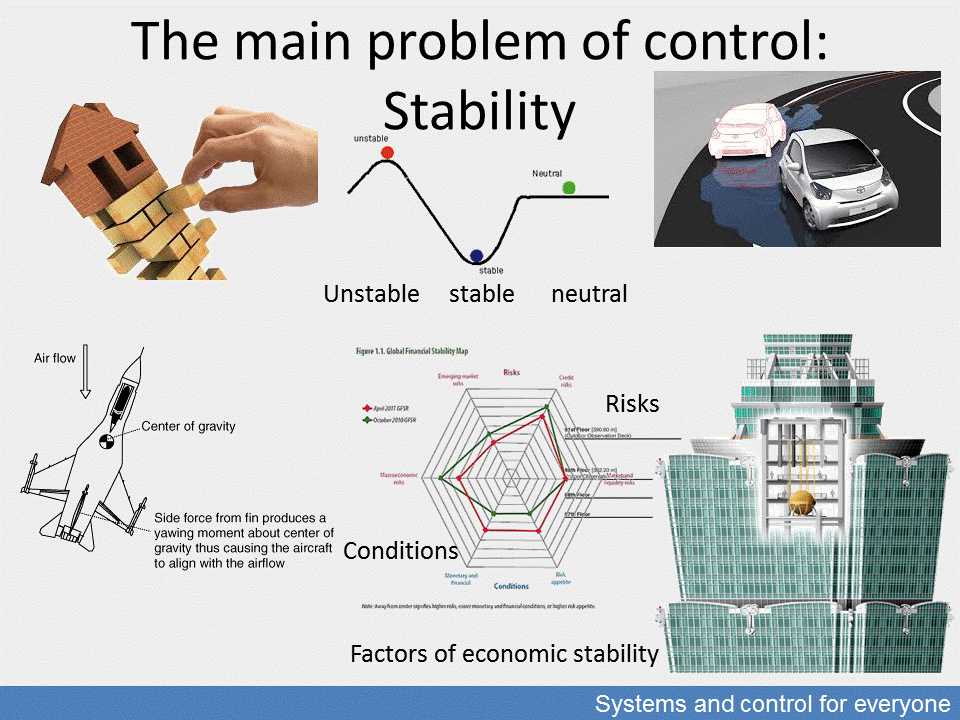

The main problem of control: Stability
A system is stable if it returns to its original position of rest or constant motion after an impulse that moved it out from such position or motion. This definition suggests that stability can be viewed from many aspects. Stability can be formulated by setting limits for the input effect and the output (bounded input-bounded output (BIBO) stability); it can be the inherent characteristic of a system; or the result of a corresponding closed-loop control. The opposite of stability is instability which causes the system to unlimitedly collapse in response to even the smallest input. Stability is a key issue in controlling systems.
Stability acts against control because it tries to resist any change. This is another evidently general characteristic which applies to vehicle control and social relations alike.
For this reason, as systems and related expectations become more and more complex, it will be increasingly important to find solutions which ensure stability and desirable changes.
The problem of closed-loop system control can only be discussed on the basis of mathematical considerations, as such control can only be implemented by analysing the dynamics and change properties of the system and actuating appropriately.