
The aim and the goal function of a control system
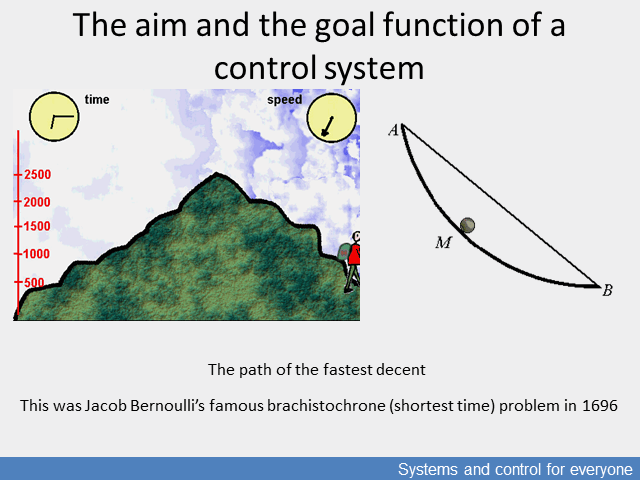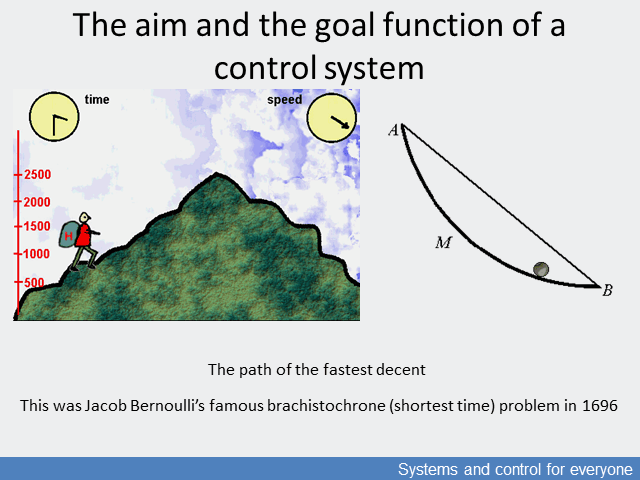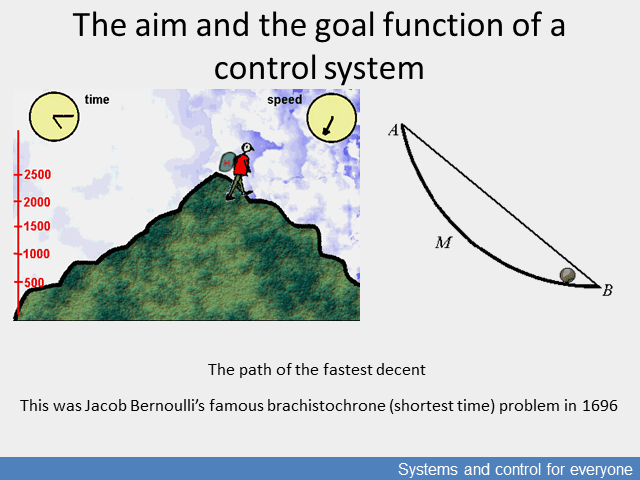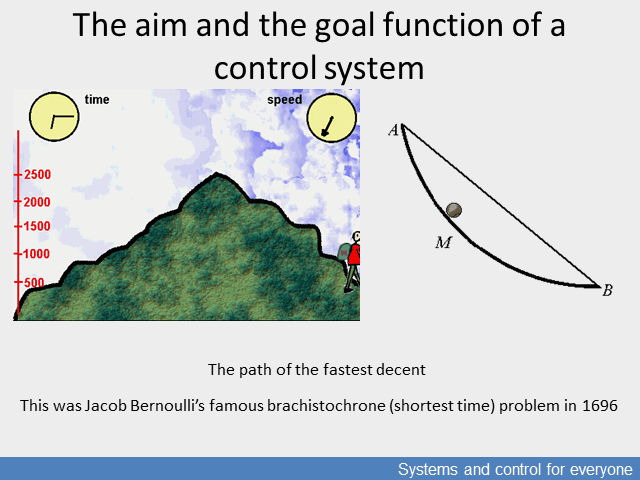
The problem had become interesting when man started to control motion. Thus, the question and its mathematical model first appeared when at the end of the 17th century Johann Bernoulli presented the brachistochrone (shortest time) problem which searched for the optimal motion, that is the route of the fastest descent path between two points if the descending body starts from an idle position. The problem was addressed by the most prominent mathematicians of the time, and this huge effort to find the solution led to variational calculus, differential calculus and the Lagrangian energy model describing change in systems. These calculi can be translated into complex multivariable processes by analogy of the motion, and into processes which can be approximated as linears by matrix calculus.
The model of the process to be controlled describes the change that leads to the goal, where we have to select the most advantageous variants: the optimums.