
State spaces and process identification
To be able to control a process, it is essential to have a certain level of understanding of the process and create its computation model. The model may be based on the representation of the (mainly physical) operation of the process or on the identification procedure calculated from the measurable input and output signals of the process. In best practice, the two approaches are continuously aligned as the model hypothesis is improved.
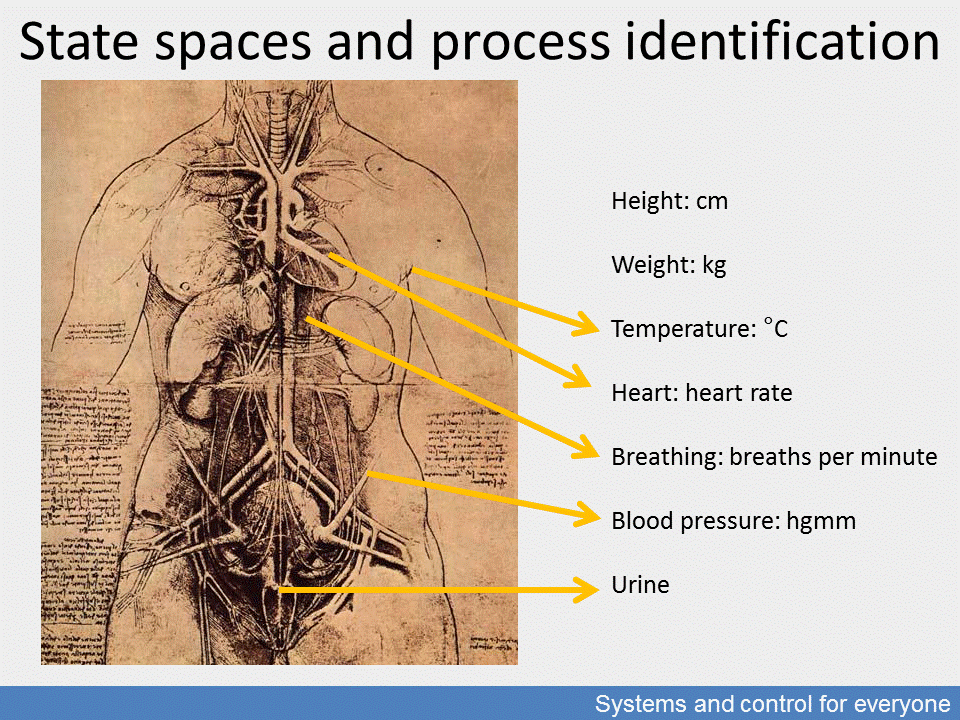
Identification is based on input-output measurement faces many difficulties and interpretation problems in more complex systems, so we mainly use state space representations which adopt a more general approach, that is, the measurement of all the state properties and their relations within the system which can be considered for the calculations. Mathematical model representation realises these state relations in analytic functional equations applied to continuous processes, or more generally, in differential operator functions.