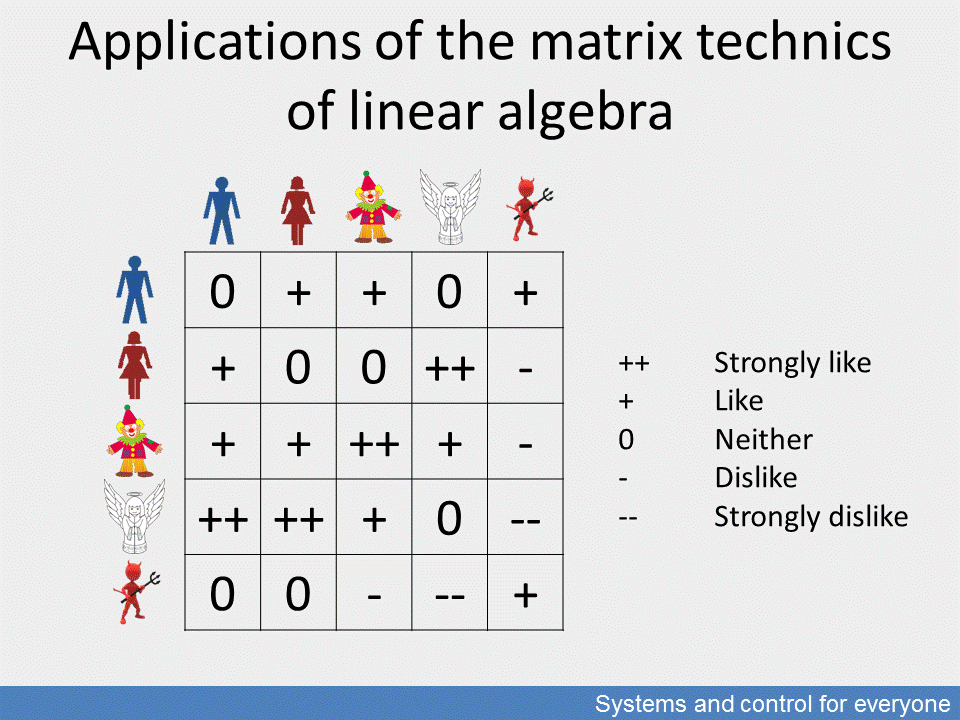

Applications of the matrix techniques of linear algebra
It is an important group consequence (also from an information technology perspective) that the matrix operations of linear algebra lead users to convenient and well-developed methods as the relations together with the option of linear superposition make all linear algebra calculations possible. It follows that two- and three-dimensional methods can be easily extended to multidimensional ones, enabling the calculation of multivariable systems as multidimensional shapes.
Stationarity allows for assuming that the statistical characteristics of the previous and the expected behaviour of the process will be identical. This way previous observations can be transposed to later behaviours. This previous possibility of observation is considered as a condition of the observability of the process and the possibility of future projection as a condition of controllability. This projection of the past into the future, and vice versa, is described by the Hankel matrices which are skew-symmetric transformations. In non-stationary processes, constantly entering new phenomena can be represented by the Toeplitz matrix. Interrelations between signals/phenomena can be handled with Gram matrices which play an important role in deciding on controllability and observability.
The single variable, linear and stationary basic model, which is free from uncertainties and disturbance signals, can be extended by modifying these model conditions. Algebra, including group theory, determines the possibilities and the strict limits of such extensions. Transformations also have to be handled within this system of possibilities and rules. This way the validity of the basic model is extended if the Hankel matrix is added functions representing the non-stationary and non-linear relations between the system input and output. The limits can be better observed by using the analytical functions which are in fact the basic methods of representations approximating the processes of real phenomena.