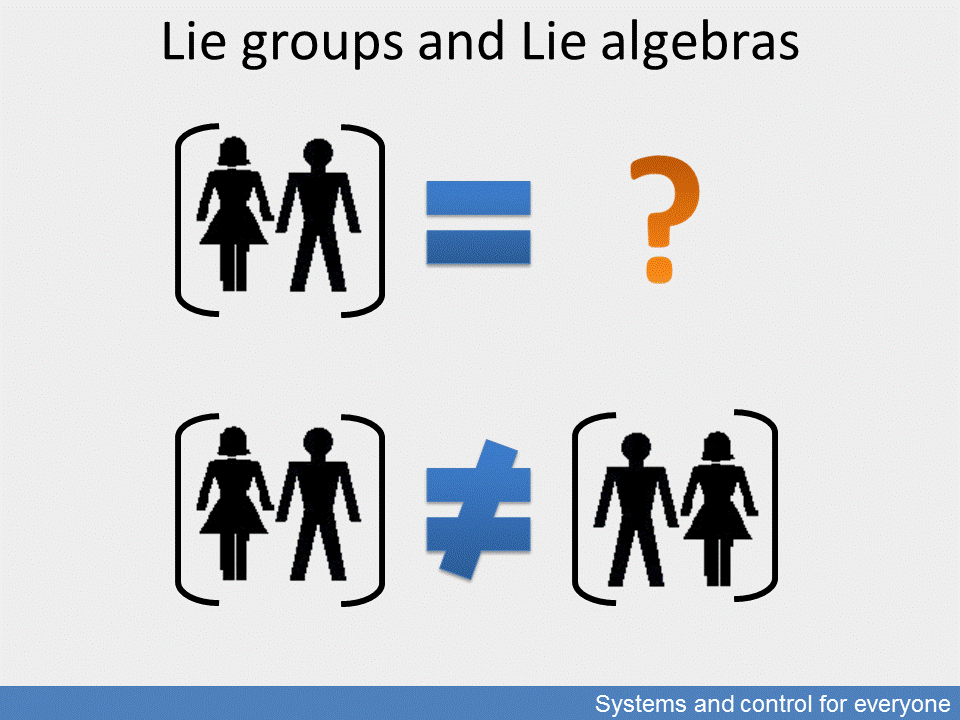
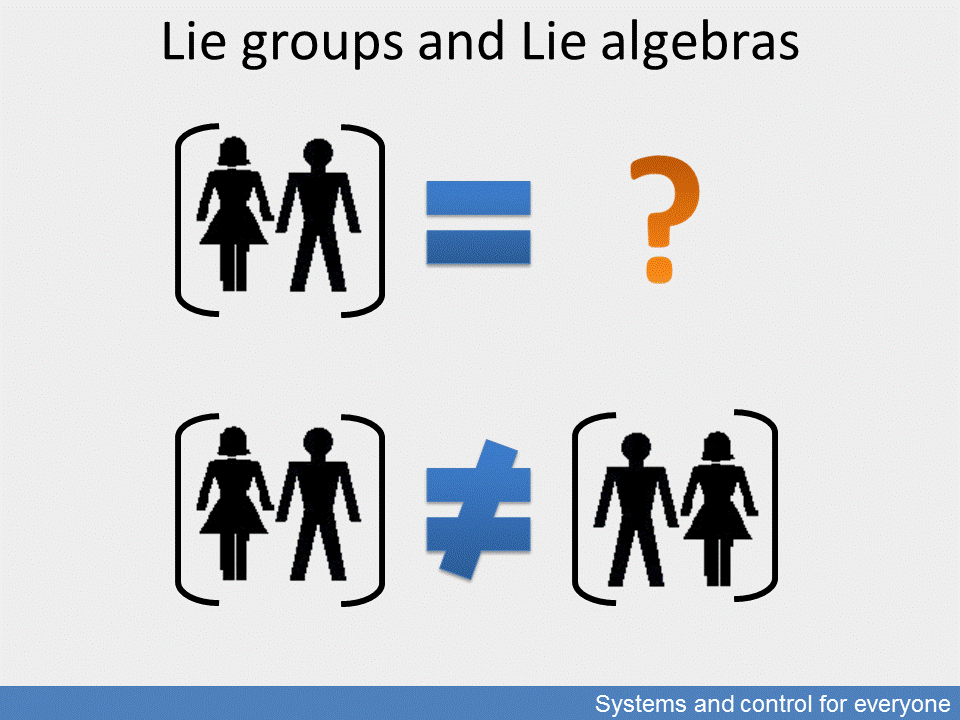
Lie groups and Lie algebras
In systems engineering calculations Lie groups and algebras play an important role. They have the remarkable characteristic that there is a property and operation describing equilibriums which originate from the anticommutative (diagonally symmetric) properties and the Lie or Poisson bracket equilibrium operations of Lie groups, and from the Jacobi equation.
Ultimately, the Hamiltonian equations, which express one of the fundamental relations of the physical world, can be described by the commutator of the Lie algebra. This represents the reversibility or irreversibility of the processes and the equilibrium relations. If the operation in brackets gives zero as a result, the examined system is in a state of equilibrium, if it gives any other value, we have to find the system elements and/or effects that break and/or restore the equilibrium.